沪教版九上26.2 特殊二次函数的图像(1) 课件(22张PPT)
文档属性
| 名称 | 沪教版九上26.2 特殊二次函数的图像(1) 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 924.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 10:57:44 | ||
图片预览





文档简介
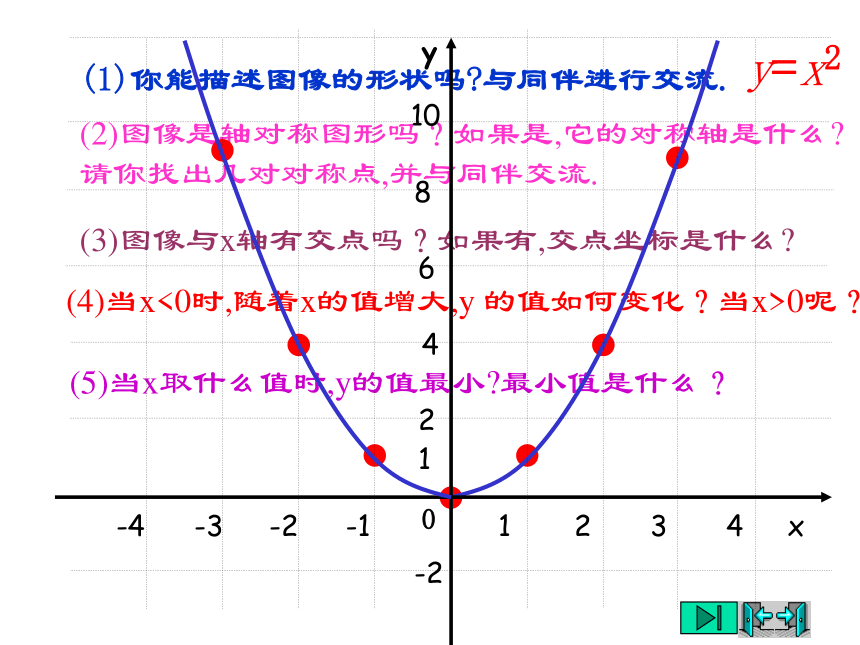
课件22张PPT。26.2(1)二次函数y=ax2的图像数形结合,直观感受1、在二次函数y=x2中,y随x的变化而变化的规律是什么?3、观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:2、你会用描点法画二次函数y=x2的图像吗?y=x2描点,连线(1)你能描述图像的形状吗?与同伴进行交流.(2)图像是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.(3)图像与x轴有交点吗?如果有,交点坐标是什么?(4)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?(5)当x取什么值时,y的值最小?最小值是什么?这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y=x2的
图像形如物体抛射
时所经过的路线,我
们把它叫做抛物线.当x<0 (在对称轴的
左侧)时,y随着x的增大而
减小. 当x>0 (在对称轴的
右侧)时, y随着x的增大而
增大. 抛物线y=x2在x轴的
上方(除顶点外),顶点
是它的最低点,开口
向上,并且向上无限
伸展;当x=0时,函数y
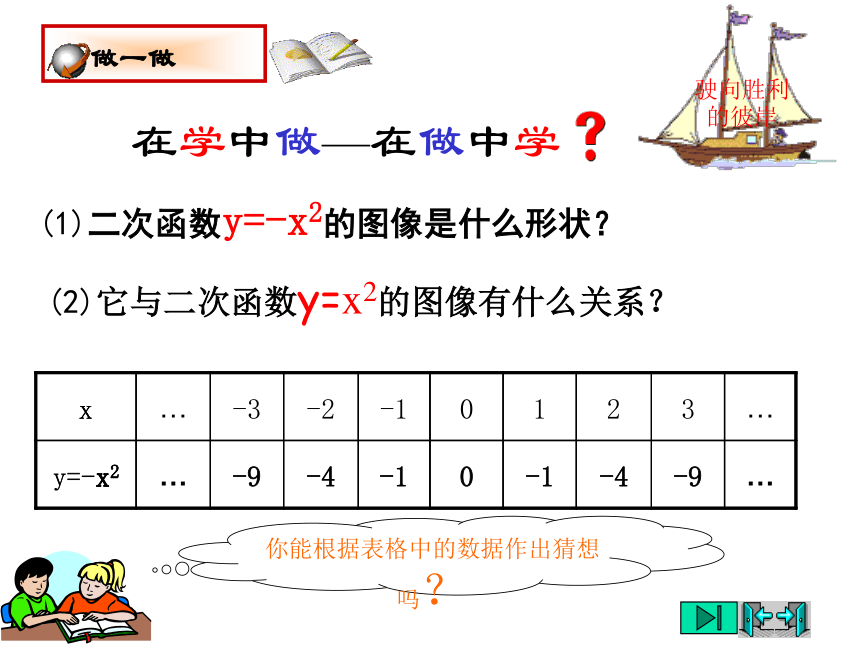
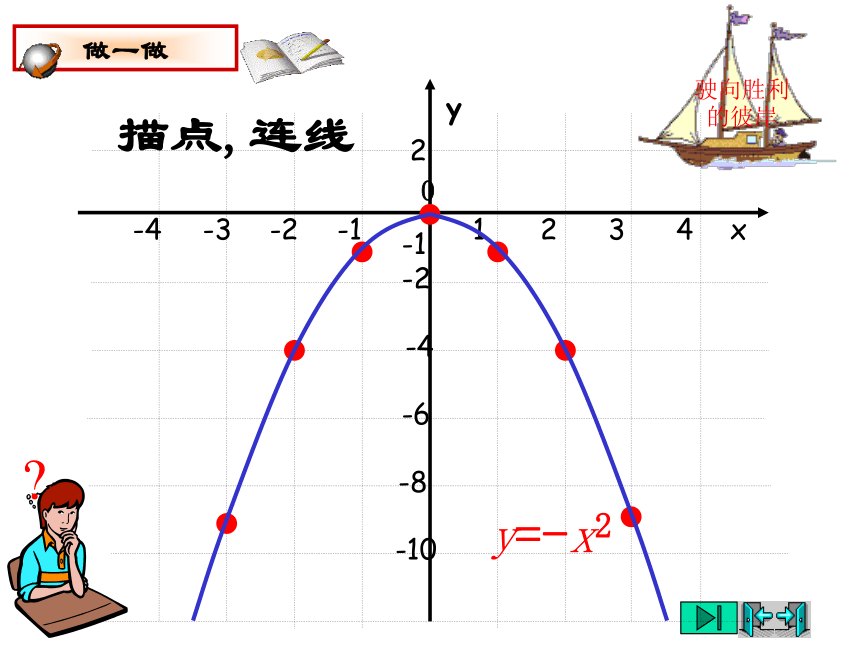
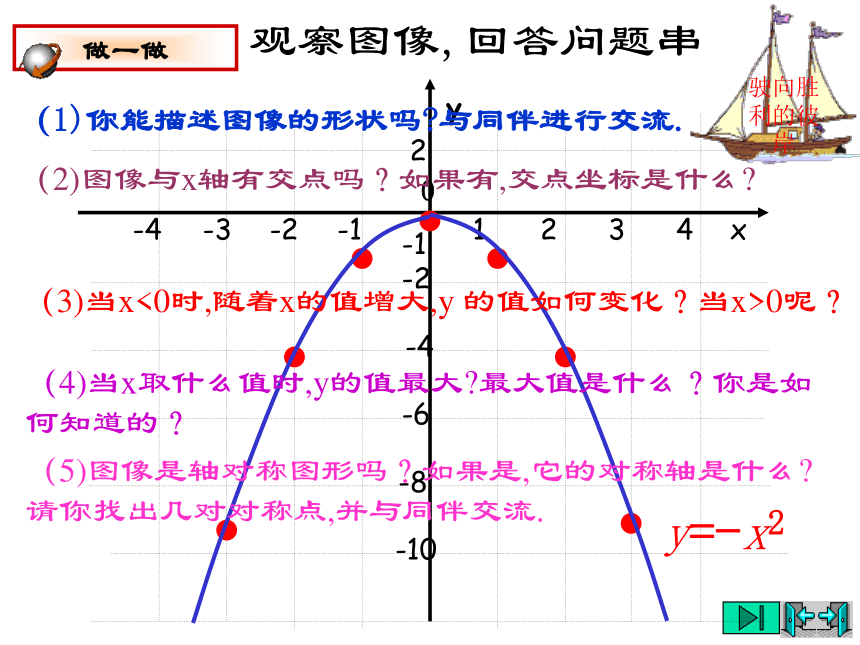
的值最小,最小值是0.在学中做—在做中学(1)二次函数y=-x2的图像是什么形状?你能根据表格中的数据作出猜想吗?驶向胜利的彼岸(2)它与二次函数y=x2的图像有什么关系?做一做驶向胜利的彼岸xy0-4-3-2-11234-10-8-6-4-22-1描点,连线y=-x2驶向胜利的彼岸观察图像,回答问题串(1)你能描述图像的形状吗?与同伴进行交流.(2)图像与x轴有交点吗?如果有,交点坐标是什么?(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?(4)当x取什么值时,y的值最大?最大值是什么?你是如何知道的?(5)图像是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.y=-x2这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y= -x2的
图像形如物体抛射
时所经过的路线,我
们把它叫做抛物线.y当x<0 (在对称轴的
左侧)时,y随着x的增大而
增大. 当x>0 (在对称轴
的右侧)时, y随着
x的增大而减小. y抛物线y= -x2在x轴的
下方(除顶点外),顶点
是它的最高点,开口
向下,并且向下无限
伸展;当x=0时,函数y
的值最大,最大值是0.看图说话函数y=ax2(a≠0)的图象和性质:y=x2y=-x2它们之间有何关系?二次函数y=ax2的性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=x2y= -x2(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:y=x2和y=-x2是y=ax2当a=±1时的特殊例子.a的符号确定着抛物线的……驶向胜利的彼岸函数y=ax2(a≠0)的图象和性质:在同一坐标系中作出函数y=x2和y=-x2的图象看图说话y=x2y=-x21.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(顶点除外),它的开口向上,并且向上无限伸展;当a<0时,抛物线y=ax2在x轴的下方(顶点除外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质我思,我进步1.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.驶向胜利的彼岸解:(1)把(-2,-8)代入y=ax2,得 -8=a(-2)2,
解得a= -2,所求函数解析式为y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上.(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
知道就做别客气2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外). (2)抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.驶向胜利的彼岸(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小01、在下列函数中①y=-2x2;②y=-2x+1;③y=x; ④y=x2,回答:
(1)______的图像是直线,______的图像是抛物线.
(2)函数______y 随着x的增大而增大.
函数______y 随着x的增大而减小.
(3)函数___的图像关于y 轴对称.函数______的图像关于原点对称.
(4)函数______有最大值为_____.函数______有最小值为______.
2、已知函数y=ax2+bx+c(a,b,c是常数).(1)若它是二次函数,则系数应满足条件____.
(2)若它是一次函数,则系数应满足条件___.(3)若它是正比例函数,则系数应满足条件__.3、已知函数y=(m2-3m) 的图像是抛物线,则函数的解析式为______,抛物线的顶点坐标为______,对称轴方程为______,开口
向______.回味无穷2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;
在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;
在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.驶向胜利的彼岸由二次函数y=x2和y=-x2知:习题26.(1) 1、2、3、4、5题结束寄语只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步. 再见
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y=x2的
图像形如物体抛射
时所经过的路线,我
们把它叫做抛物线.当x<0 (在对称轴的
左侧)时,y随着x的增大而
减小. 当x>0 (在对称轴的
右侧)时, y随着x的增大而
增大. 抛物线y=x2在x轴的
上方(除顶点外),顶点
是它的最低点,开口
向上,并且向上无限
伸展;当x=0时,函数y
的值最小,最小值是0.在学中做—在做中学(1)二次函数y=-x2的图像是什么形状?你能根据表格中的数据作出猜想吗?驶向胜利的彼岸(2)它与二次函数y=x2的图像有什么关系?做一做驶向胜利的彼岸xy0-4-3-2-11234-10-8-6-4-22-1描点,连线y=-x2驶向胜利的彼岸观察图像,回答问题串(1)你能描述图像的形状吗?与同伴进行交流.(2)图像与x轴有交点吗?如果有,交点坐标是什么?(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?(4)当x取什么值时,y的值最大?最大值是什么?你是如何知道的?(5)图像是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.y=-x2这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y= -x2的
图像形如物体抛射
时所经过的路线,我
们把它叫做抛物线.y当x<0 (在对称轴的
左侧)时,y随着x的增大而
增大. 当x>0 (在对称轴
的右侧)时, y随着
x的增大而减小. y抛物线y= -x2在x轴的
下方(除顶点外),顶点
是它的最高点,开口
向下,并且向下无限
伸展;当x=0时,函数y
的值最大,最大值是0.看图说话函数y=ax2(a≠0)的图象和性质:y=x2y=-x2它们之间有何关系?二次函数y=ax2的性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=x2y= -x2(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:y=x2和y=-x2是y=ax2当a=±1时的特殊例子.a的符号确定着抛物线的……驶向胜利的彼岸函数y=ax2(a≠0)的图象和性质:在同一坐标系中作出函数y=x2和y=-x2的图象看图说话y=x2y=-x21.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(顶点除外),它的开口向上,并且向上无限伸展;当a<0时,抛物线y=ax2在x轴的下方(顶点除外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质我思,我进步1.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.驶向胜利的彼岸解:(1)把(-2,-8)代入y=ax2,得 -8=a(-2)2,
解得a= -2,所求函数解析式为y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上.(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
知道就做别客气2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外). (2)抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.驶向胜利的彼岸(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小01、在下列函数中①y=-2x2;②y=-2x+1;③y=x; ④y=x2,回答:
(1)______的图像是直线,______的图像是抛物线.
(2)函数______y 随着x的增大而增大.
函数______y 随着x的增大而减小.
(3)函数___的图像关于y 轴对称.函数______的图像关于原点对称.
(4)函数______有最大值为_____.函数______有最小值为______.
2、已知函数y=ax2+bx+c(a,b,c是常数).(1)若它是二次函数,则系数应满足条件____.
(2)若它是一次函数,则系数应满足条件___.(3)若它是正比例函数,则系数应满足条件__.3、已知函数y=(m2-3m) 的图像是抛物线,则函数的解析式为______,抛物线的顶点坐标为______,对称轴方程为______,开口
向______.回味无穷2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;
在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;
在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.驶向胜利的彼岸由二次函数y=x2和y=-x2知:习题26.(1) 1、2、3、4、5题结束寄语只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步. 再见
