人教B版(2019)必修(第二册)第四章 指数函数、对数函数与幂函数4.5.3函数模型的应用(1)(21张PPT)
文档属性
| 名称 | 人教B版(2019)必修(第二册)第四章 指数函数、对数函数与幂函数4.5.3函数模型的应用(1)(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
我国著名数学家华罗庚指出:
“宇宙之大,粒子之微,火箭之速,化工之巧,
地球之变,生物之谜,日用之繁,无处不用
数学。”
数 学 无 处 不 在 !
飞行器设计
网络安全
海洋遥测数据处理
艾宾浩斯记忆遗忘曲线
马家沟的芹菜
Black-Scholes 期权定价
Nash 经济对策
Markowitz:证券组合选择理论
Kantorovich资源最优配置理论
Leontief 投入产出方法及其对重要经济问题的应用
Klein 宏观经济计量模型
Tobin 金融市场及其支出决策,就业,生产和价格的关系的分析
Solow 经济增长理论
Haavlmo 计量经济学的概率论基础和联立经济结构分析
Allias 市场和资源的有效利用理论
Mundell 不同汇率下的货币政策的分析及最优货币流通区域的研究
North 美国经济增长的数学模型
Becker 将微观经济分析的方法推广到人类行为及相互作用
Modiglini 储蓄和金融市场的先驱性贡献
Ohlin-Meade 国际贸易和国际资本运动的突破性贡献
Friedman 消费分析,货币理论及稳定化政策的复杂性研究
诺贝尔经济学奖与数学
数 学 无 处 不 在 !
本节课内容
4.5.3函数模型的应用
授课人: 李敏
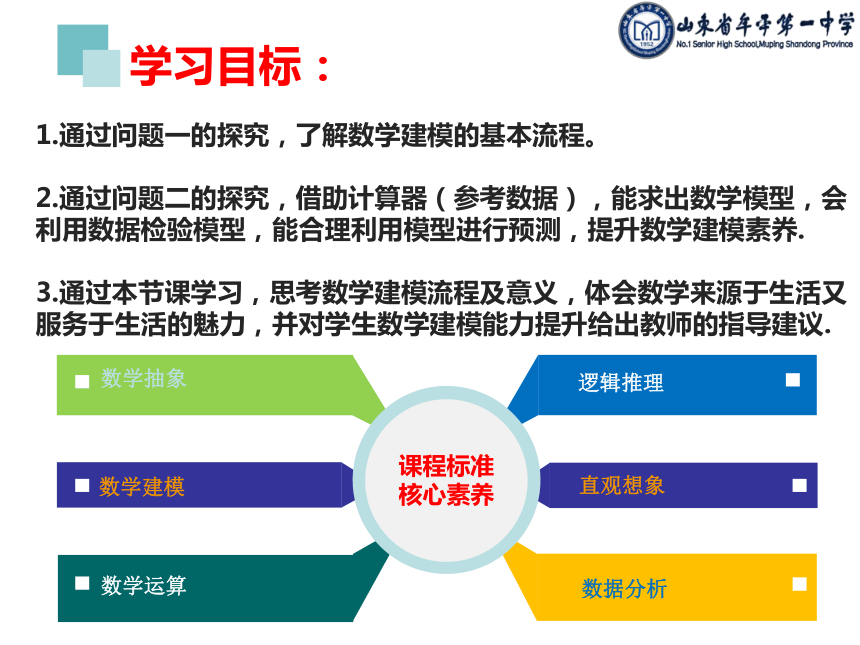
1.通过问题一的探究,了解数学建模的基本流程。
2.通过问题二的探究,借助计算器(参考数据),能求出数学模型,会利用数据检验模型,能合理利用模型进行预测,提升数学建模素奍.
3.通过本节课学习,思考数学建模流程及意义,体会数学来源于生活又服务于生活的魅力,并对学生数学建模能力提升给出教师的指导建议.
学习目标:
数学抽象
数学建模
数学运算
逻辑推理
直观想象
数据分析
甲乙两地相距750千米,船从甲到乙顺水航行需30小时,
从乙到甲逆水航行需50小时,问船的速度是多少?
问题一:
你碰到过的数学模型——“航行问题”
甲乙两地相距750千米,船从甲到乙顺水航行需30小时,
从乙到甲逆水航行需50小时,问船的速度是多少?
问题一:
你碰到过的数学模型——“航行问题”
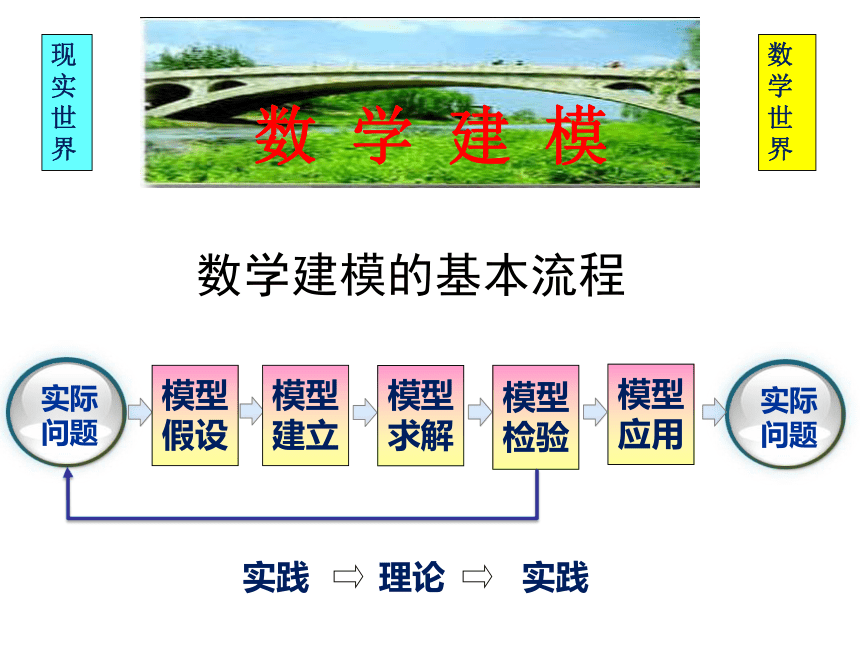
数学建模的基本流程
人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为制定一系列的相关政策提供依据.早在1798年,英国经济学家马尔萨斯(T.R . Malthus,1766-1834)就提出了自然状态下的人口增长模型:y=y0ert. 其中t表示经过的时间, y0表示t=0时的人口数, r表示人口的年平均增长率.
(1)根据国家统计局网站公布的数据,我国1950年末、1959年末的人口总数分别为55196万和67107万.
根据这些数据,用马尔萨斯人口增长模型建立我国1950~1959年期间的具体人口增长模型.
( 1950年末、1959年末的人口总数分别用a,b表示,试用含a,b的式子写出模型)
问题二:
(2)利用(1)中的模型计算1951~1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,检验所得模型与实际人口数据是否相符.(以小组形式:组员间思考交流检验方法,不必进行计算.)
年份 1951 1952 1953 1954 1955 1956 1957 1958
实际人口数/万 56300 57482 58796 60266 61465 62828 64563 65994
计算所得人口总数/万 y1 y2 y3 y4 y5 y6 y7 y8
(2)利用(1)中的模型计算1951~1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,检验所得模型与实际人口数据是否相符.(以小组形式:组员间思考交流检验方法,不必进行计算.)
年份 1951 1952 1953 1954 1955 1956 1957 1958
实际人口数/万 56300 57482 58796 60266 61465 62828 64563 65994
计算所得人口总数/万 56417 57665 58940 60243 61576 62938 64330 65753
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
(只需写出算式)
y0ert≥13 ?
y0ert≥130000 ?
y0ert=13 ?
y0ert=130000 ?
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
若据y0ert=130000求得t≈39.15,那么在哪一年,我国的人口数达到13亿?
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
若据y0ert=130000求得t≈39.15,那么在哪一年,我国的人口数达到13亿?
思考1:如果按照前面所得到的1950—1959年我国人口的马尔萨斯模型:y=y0ert可以计算出2019年底我国的人口总数为24.4亿;到2051年底我国人口总数为49亿人.你有何感想?
思考2:实际上,我国1990年的人口数为11.43亿,直到2005年才突破了13亿,对此,你有什么看法?
拓展思考:
1. 1650年世界人口为5亿,当时人口的年增长率为0.3%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1650年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
1970年世界人口为36亿,当时人口的年增长率为2.1%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1970年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
拓展思考:
1. 1650年世界人口为5亿,当时人口的年增长率为0.3%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1650年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
1970年世界人口为36亿,当时人口的年增长率为2.1%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1970年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
实际上,1850年以前世界人口就超过了10亿;
而2004年世界人口还没有达到72亿,你对同样的模型得出的两个结果有何看法?
再反思:
请同学们再次回顾一下本节课的问题一、问题二
问题一:数学建模的基本流程;
问题二:(1)马尔萨斯人口模型的求解、检验、应用
当中的细节问题;
(2)人口模型对现实的意义。
建议:如何培养数学建模能力?
(3)培养数学应用意识,丰富数学建模手段/工具
(2)亲自动手,认真做几个实际题目.
(1)学习、分析、评价、改进别人作过的模型.
(4)参加有关数学建模的竞赛
1.通过问题一的探究,了解数学建模的基本流程。
2.通过问题二的探究,借助计算器(表格),能求出数学模型,会利用数据检验模型,能合理利用模型进行预测,提升数学建模素奍.
3.通过本节课学习,思考数学建模的意义,体会数学来源于生活又服务于生活的魅力,并对学生数学建模能力提升给出教师的指导建议.
回扣目标:
数学抽象
数学建模
数学运算
逻辑推理
直观想象
数据分析
课后作业:
1.完成课本第149页例4;第150页课后练习3;
2.请同学们以我们平度的马家沟芹菜产后直接销售、 冷风库储藏后销售、网络销售作一研究。请以小组为单位,收集整理相关数据,结合本节所学数学建模知识,撰写一个研究性学习报告,利用我们所学的数学知识给我们平度的人民给出一个有说服力的建议。
3.课外阅读:《中学数学建模与探究》《数学模型》
我国著名数学家华罗庚指出:
“宇宙之大,粒子之微,火箭之速,化工之巧,
地球之变,生物之谜,日用之繁,无处不用
数学。”
数 学 无 处 不 在 !
飞行器设计
网络安全
海洋遥测数据处理
艾宾浩斯记忆遗忘曲线
马家沟的芹菜
Black-Scholes 期权定价
Nash 经济对策
Markowitz:证券组合选择理论
Kantorovich资源最优配置理论
Leontief 投入产出方法及其对重要经济问题的应用
Klein 宏观经济计量模型
Tobin 金融市场及其支出决策,就业,生产和价格的关系的分析
Solow 经济增长理论
Haavlmo 计量经济学的概率论基础和联立经济结构分析
Allias 市场和资源的有效利用理论
Mundell 不同汇率下的货币政策的分析及最优货币流通区域的研究
North 美国经济增长的数学模型
Becker 将微观经济分析的方法推广到人类行为及相互作用
Modiglini 储蓄和金融市场的先驱性贡献
Ohlin-Meade 国际贸易和国际资本运动的突破性贡献
Friedman 消费分析,货币理论及稳定化政策的复杂性研究
诺贝尔经济学奖与数学
数 学 无 处 不 在 !
本节课内容
4.5.3函数模型的应用
授课人: 李敏
1.通过问题一的探究,了解数学建模的基本流程。
2.通过问题二的探究,借助计算器(参考数据),能求出数学模型,会利用数据检验模型,能合理利用模型进行预测,提升数学建模素奍.
3.通过本节课学习,思考数学建模流程及意义,体会数学来源于生活又服务于生活的魅力,并对学生数学建模能力提升给出教师的指导建议.
学习目标:
数学抽象
数学建模
数学运算
逻辑推理
直观想象
数据分析
甲乙两地相距750千米,船从甲到乙顺水航行需30小时,
从乙到甲逆水航行需50小时,问船的速度是多少?
问题一:
你碰到过的数学模型——“航行问题”
甲乙两地相距750千米,船从甲到乙顺水航行需30小时,
从乙到甲逆水航行需50小时,问船的速度是多少?
问题一:
你碰到过的数学模型——“航行问题”
数学建模的基本流程
人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为制定一系列的相关政策提供依据.早在1798年,英国经济学家马尔萨斯(T.R . Malthus,1766-1834)就提出了自然状态下的人口增长模型:y=y0ert. 其中t表示经过的时间, y0表示t=0时的人口数, r表示人口的年平均增长率.
(1)根据国家统计局网站公布的数据,我国1950年末、1959年末的人口总数分别为55196万和67107万.
根据这些数据,用马尔萨斯人口增长模型建立我国1950~1959年期间的具体人口增长模型.
( 1950年末、1959年末的人口总数分别用a,b表示,试用含a,b的式子写出模型)
问题二:
(2)利用(1)中的模型计算1951~1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,检验所得模型与实际人口数据是否相符.(以小组形式:组员间思考交流检验方法,不必进行计算.)
年份 1951 1952 1953 1954 1955 1956 1957 1958
实际人口数/万 56300 57482 58796 60266 61465 62828 64563 65994
计算所得人口总数/万 y1 y2 y3 y4 y5 y6 y7 y8
(2)利用(1)中的模型计算1951~1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,检验所得模型与实际人口数据是否相符.(以小组形式:组员间思考交流检验方法,不必进行计算.)
年份 1951 1952 1953 1954 1955 1956 1957 1958
实际人口数/万 56300 57482 58796 60266 61465 62828 64563 65994
计算所得人口总数/万 56417 57665 58940 60243 61576 62938 64330 65753
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
(只需写出算式)
y0ert≥13 ?
y0ert≥130000 ?
y0ert=13 ?
y0ert=130000 ?
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
若据y0ert=130000求得t≈39.15,那么在哪一年,我国的人口数达到13亿?
(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
若据y0ert=130000求得t≈39.15,那么在哪一年,我国的人口数达到13亿?
思考1:如果按照前面所得到的1950—1959年我国人口的马尔萨斯模型:y=y0ert可以计算出2019年底我国的人口总数为24.4亿;到2051年底我国人口总数为49亿人.你有何感想?
思考2:实际上,我国1990年的人口数为11.43亿,直到2005年才突破了13亿,对此,你有什么看法?
拓展思考:
1. 1650年世界人口为5亿,当时人口的年增长率为0.3%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1650年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
1970年世界人口为36亿,当时人口的年增长率为2.1%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1970年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
拓展思考:
1. 1650年世界人口为5亿,当时人口的年增长率为0.3%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1650年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
1970年世界人口为36亿,当时人口的年增长率为2.1%,(1)据此写出马尔萨斯人口模型;
(2)据此模型预测什么时候世界人口是1970年的2倍?
(参考数据:ln2=0.6931, ln3=1.0986)
实际上,1850年以前世界人口就超过了10亿;
而2004年世界人口还没有达到72亿,你对同样的模型得出的两个结果有何看法?
再反思:
请同学们再次回顾一下本节课的问题一、问题二
问题一:数学建模的基本流程;
问题二:(1)马尔萨斯人口模型的求解、检验、应用
当中的细节问题;
(2)人口模型对现实的意义。
建议:如何培养数学建模能力?
(3)培养数学应用意识,丰富数学建模手段/工具
(2)亲自动手,认真做几个实际题目.
(1)学习、分析、评价、改进别人作过的模型.
(4)参加有关数学建模的竞赛
1.通过问题一的探究,了解数学建模的基本流程。
2.通过问题二的探究,借助计算器(表格),能求出数学模型,会利用数据检验模型,能合理利用模型进行预测,提升数学建模素奍.
3.通过本节课学习,思考数学建模的意义,体会数学来源于生活又服务于生活的魅力,并对学生数学建模能力提升给出教师的指导建议.
回扣目标:
数学抽象
数学建模
数学运算
逻辑推理
直观想象
数据分析
课后作业:
1.完成课本第149页例4;第150页课后练习3;
2.请同学们以我们平度的马家沟芹菜产后直接销售、 冷风库储藏后销售、网络销售作一研究。请以小组为单位,收集整理相关数据,结合本节所学数学建模知识,撰写一个研究性学习报告,利用我们所学的数学知识给我们平度的人民给出一个有说服力的建议。
3.课外阅读:《中学数学建模与探究》《数学模型》
