苏教数学五下《7.3.用转化的策略解决问题练习》课件(共39张PPT)
文档属性
| 名称 | 苏教数学五下《7.3.用转化的策略解决问题练习》课件(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 19:36:21 | ||
图片预览


文档简介
(共39张PPT)
解决问题的策略
——转化的策略
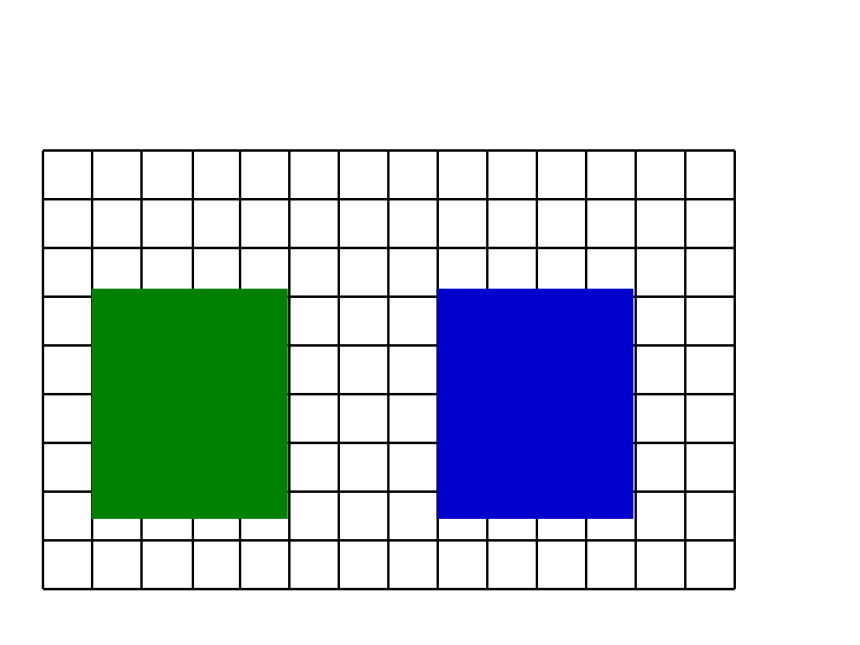
比一比,谁的面积大?
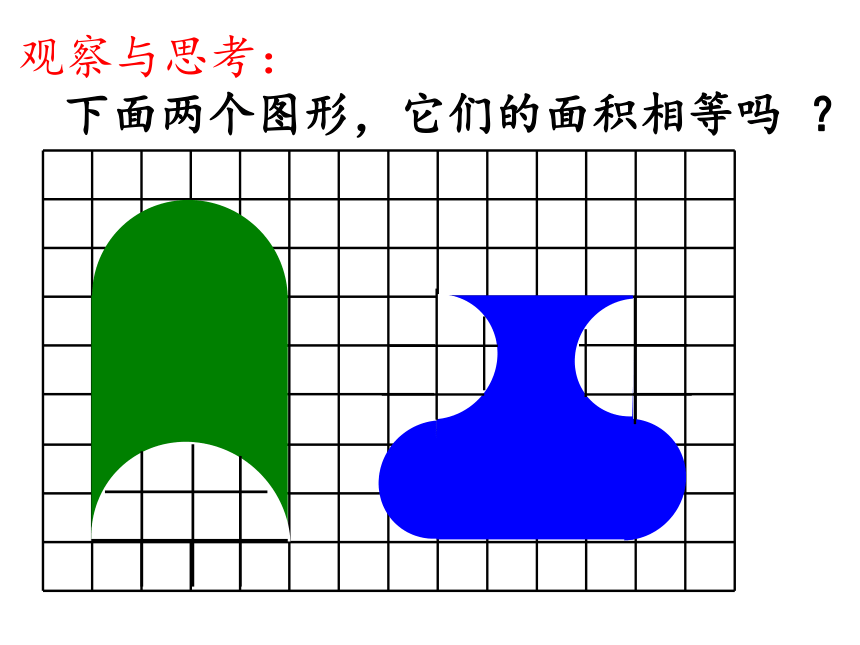
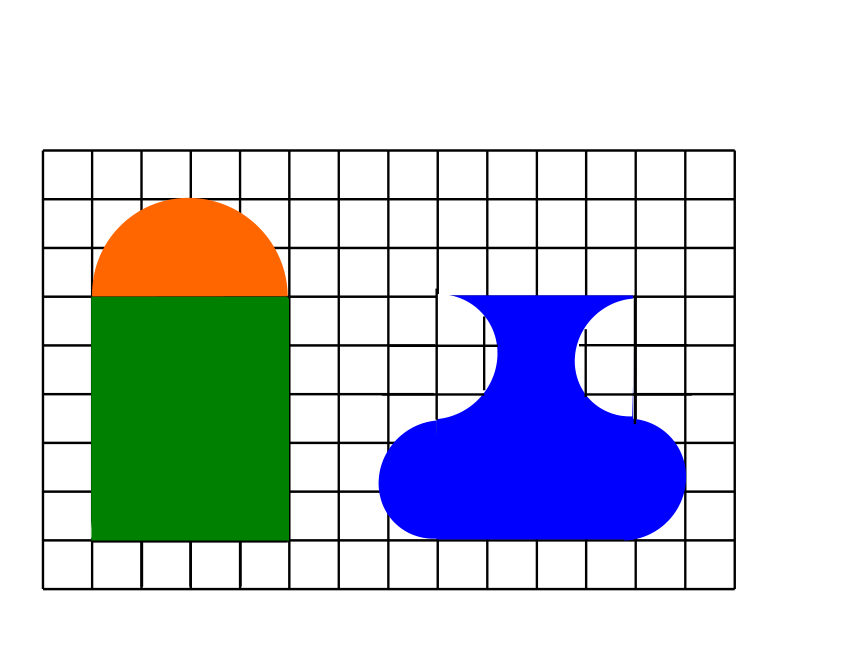
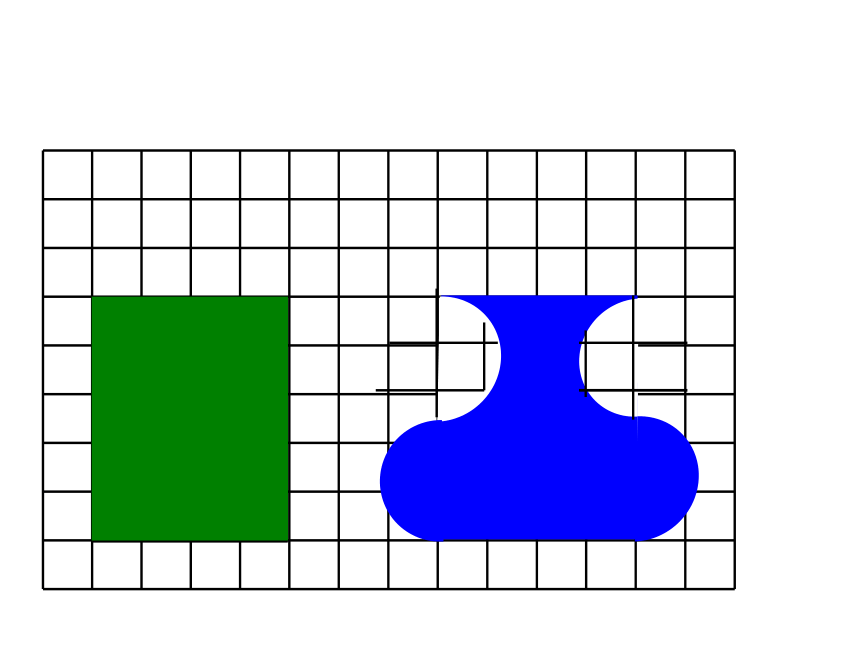
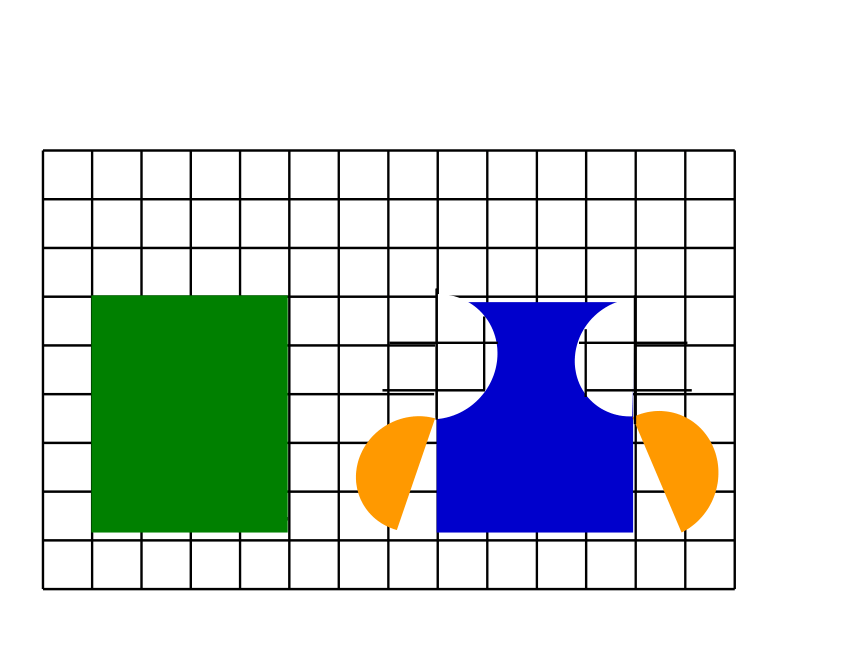
观察与思考:
下面两个图形,它们的面积相等吗 ?
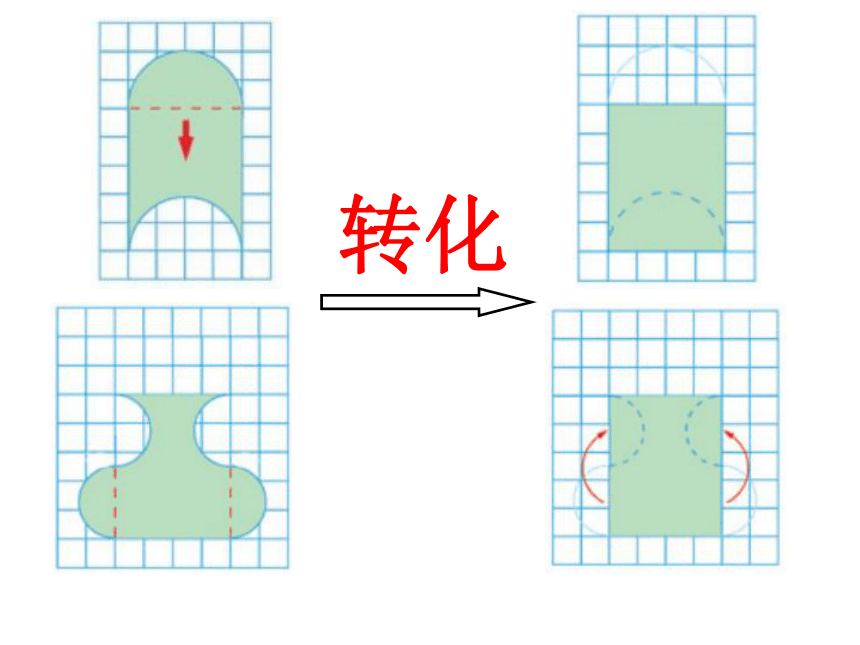
转化
1、解决例1提出的问题,我们应用了什么策略?
平移,旋转
2、用什么方法把不规则图形转化成规则图形?
转化
3、转化后的图形和转化前比,什么变了?什么没变?
形状变了,大小没变
探索新知
解题时,往往不对问题进行正面的攻击,而是将它不断变形,直至转化为已经能够解决的问题。
——匈牙利著名数学家 路莎·彼得
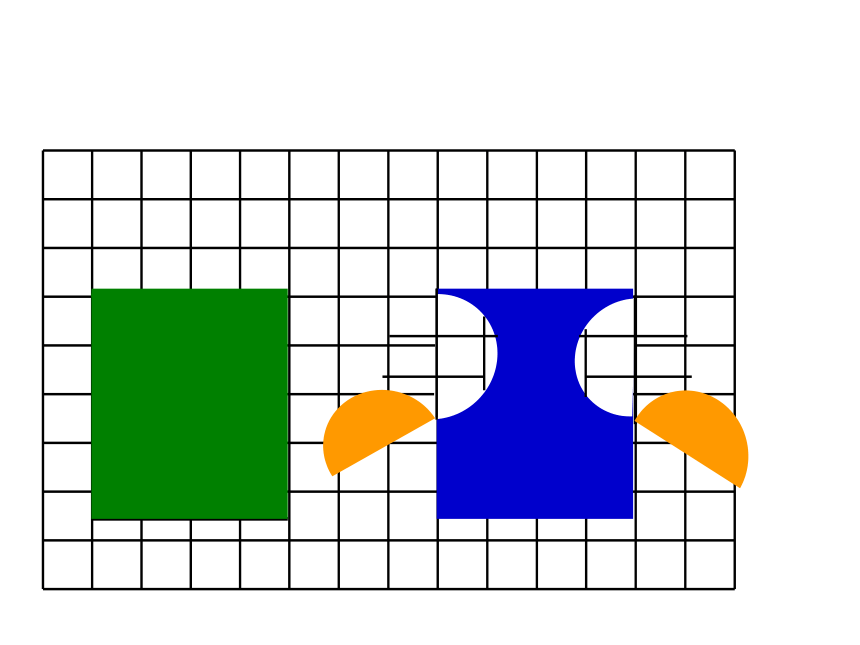
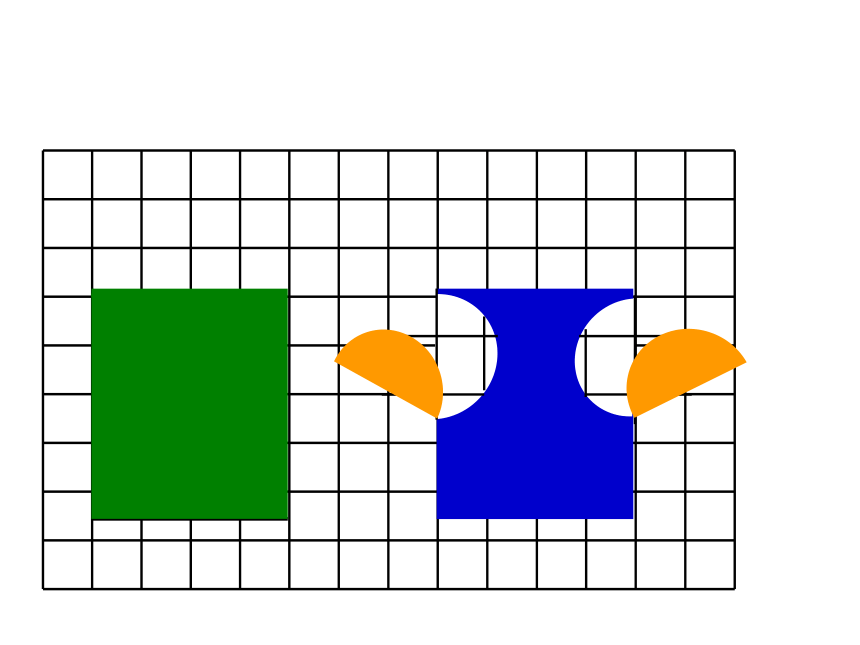
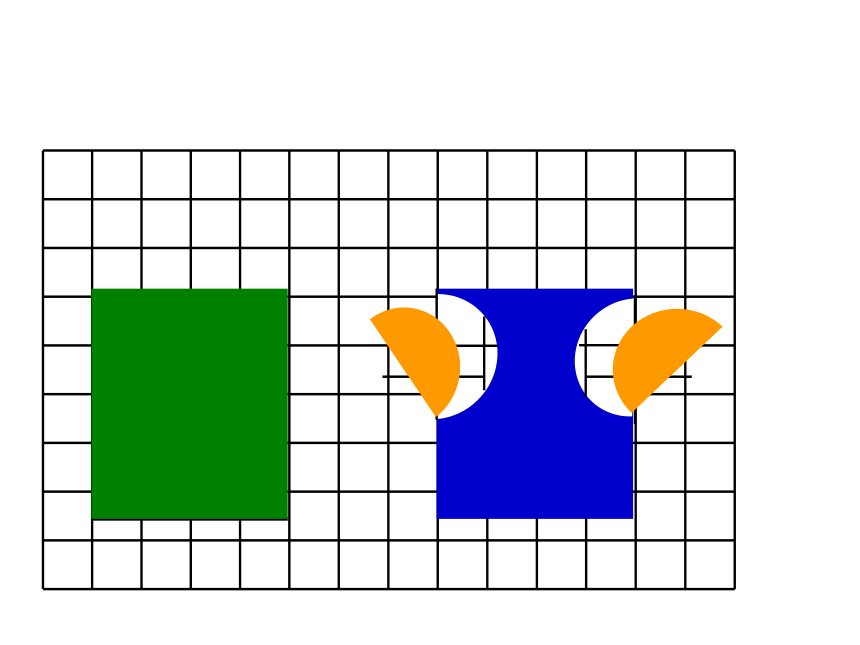
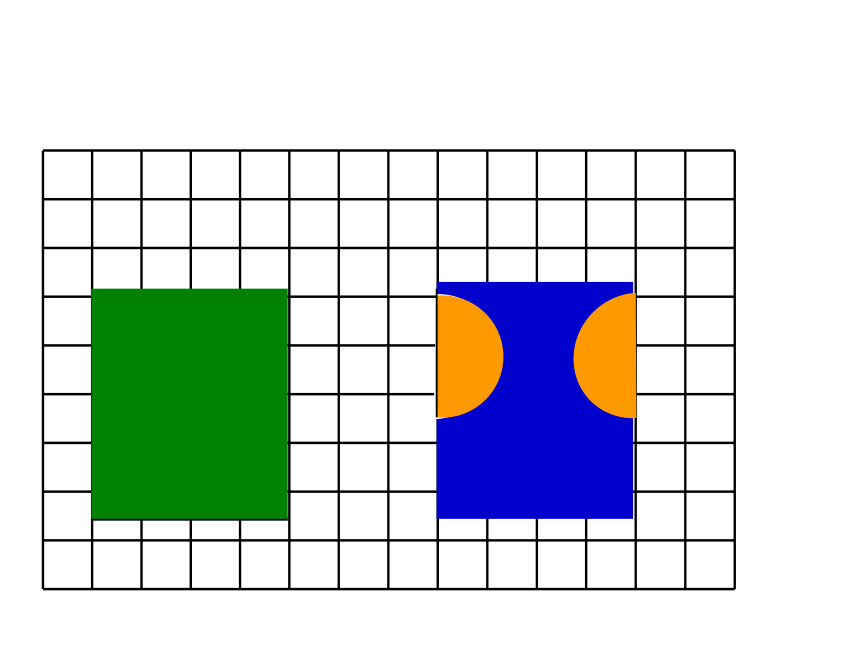
用分数表示各图中的涂色部分。
用分数表示图中的涂色部分。
1
4
旋转
用分数表示图中的涂色部分。
1
2
用分数表示图中的涂色部分。
1
2
平移
用分数表示图中的涂色部分。
等值
用分数表示图中的涂色部分。
割补
用分数表示图中的涂色部分。
回忆:
哪些知识的学习中运用到了转化?把什么转化成什么?
价值
图形中的转化
回
乘
图形中的转化
异分母分数
加减法
同分母分数加减法
计算中的转化:
小 数 乘 法
整 数 乘 法
3.25×1.3
325×13
计算中的转化
除数是小数的除法
除数是整数的除法
4.76÷ 2.4
47.6÷ 24
计算中的转化
小 数 乘 法
整 数 乘 法
异分母分数加减法
同分母分数加减法
……
本
平
旋转
平移
割补
规律、性质、法则……
典题精讲
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都 相等)。这两个图案的面积相等吗?为什么 ?
专项练习:平移
这两个图案的面积相等。
因为第二个图案可以通过第一个图案平移得到,平移后长直条和短直条的长和宽都没有变化。
典题精讲
1、观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
下边图形的周长怎么求?
下边图形的周长怎么求?
面积能这样转化吗?
左图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
40÷4=10(厘米)
10×10=100(平方厘米)
答:整个图形的面积是100平方厘米。
综合练习:
一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
45米
27米
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米。
综合练习:
解决问题的策略
——转化的策略
比一比,谁的面积大?
观察与思考:
下面两个图形,它们的面积相等吗 ?
转化
1、解决例1提出的问题,我们应用了什么策略?
平移,旋转
2、用什么方法把不规则图形转化成规则图形?
转化
3、转化后的图形和转化前比,什么变了?什么没变?
形状变了,大小没变
探索新知
解题时,往往不对问题进行正面的攻击,而是将它不断变形,直至转化为已经能够解决的问题。
——匈牙利著名数学家 路莎·彼得
用分数表示各图中的涂色部分。
用分数表示图中的涂色部分。
1
4
旋转
用分数表示图中的涂色部分。
1
2
用分数表示图中的涂色部分。
1
2
平移
用分数表示图中的涂色部分。
等值
用分数表示图中的涂色部分。
割补
用分数表示图中的涂色部分。
回忆:
哪些知识的学习中运用到了转化?把什么转化成什么?
价值
图形中的转化
回
乘
图形中的转化
异分母分数
加减法
同分母分数加减法
计算中的转化:
小 数 乘 法
整 数 乘 法
3.25×1.3
325×13
计算中的转化
除数是小数的除法
除数是整数的除法
4.76÷ 2.4
47.6÷ 24
计算中的转化
小 数 乘 法
整 数 乘 法
异分母分数加减法
同分母分数加减法
……
本
平
旋转
平移
割补
规律、性质、法则……
典题精讲
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都 相等)。这两个图案的面积相等吗?为什么 ?
专项练习:平移
这两个图案的面积相等。
因为第二个图案可以通过第一个图案平移得到,平移后长直条和短直条的长和宽都没有变化。
典题精讲
1、观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
下边图形的周长怎么求?
下边图形的周长怎么求?
面积能这样转化吗?
左图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
40÷4=10(厘米)
10×10=100(平方厘米)
答:整个图形的面积是100平方厘米。
综合练习:
一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
45米
27米
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米。
综合练习:
