沪教版 高中物理共同必修1教学课件- 2.4 匀变速直线运动规律的应用(共26张PPT)
文档属性
| 名称 | 沪教版 高中物理共同必修1教学课件- 2.4 匀变速直线运动规律的应用(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-12 14:59:44 | ||
图片预览








文档简介
(共26张PPT)
匀变速直线运动规律的应用
思考:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,他运动的加速度大小为多少?
?
一、推导公式:速度与位移的关系
式中四个量都是矢量,都有正负
不涉及到时间t,用这个公式方便
例题:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,他运动的加速度大小为多少?通过这段山坡需用多长时间?
练习1.某飞机着陆时的速度为216km/h,随后匀减速滑行,加速度大小是2m/s2,机场跑道至少要多少米飞机才能安全着陆?
练习2.通过测试得知某型号的卡车在某种路面上急刹车时加速度大小是5m/s2。如果要求它在这种路面上行驶时在22.5m内必须停下,它的行驶速度不能超过多少?
思考:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,通过这段山坡需用多长时间?
?
V
0
t
t
V0
vt
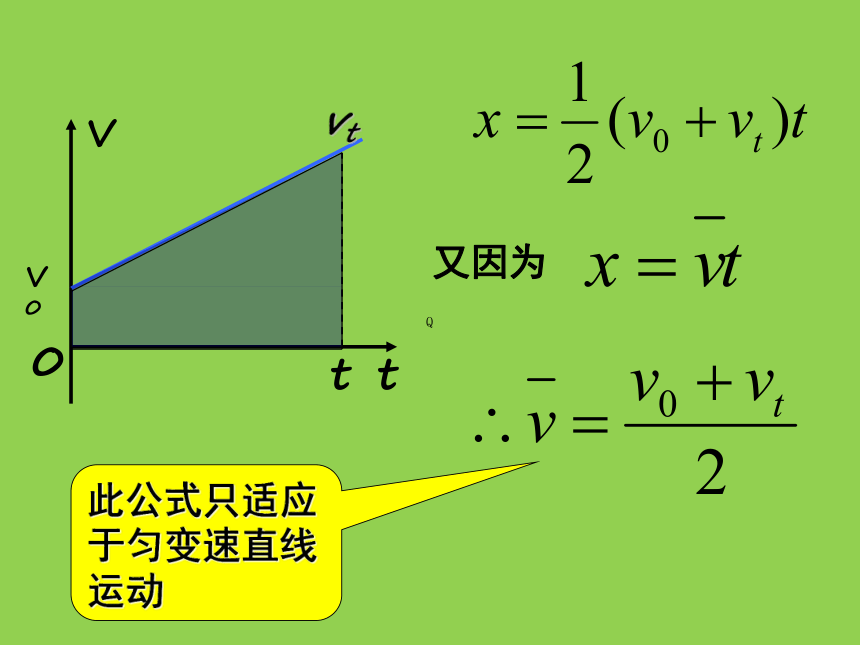
又因为
此公式只适应于匀变速直线运动
二、补充公式:
——匀变速直线运动的平均速度公式
不涉及加速度a
例题:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,通过这段山坡需用多长时间?
练习:骑自行车的人原来的速度是3m/s,下坡时做匀加速直线运动,通过50m的坡路后速度达到5m/s,求下坡所用时间和加速度的大小。
五个基本公式
加速度公式
速度公式
位移公式
速度与位移公式
平均速度公式
(1)1s末、2s末、 3s末……ns末的速度之比为多少?
(2)1s内、2s内、 3s内……ns内的位移之比为多少?
(3)第1s内、第2s内、第 3s内……第ns内的位移之比为多少?
(4)第1个x、第2个x、第 3个x……第n个x相邻相等位移的时间之比为多少?
1:2:3:…:n
1:4:9:…:n2
1:3:5:…:2n-1
三、 初速度为0的匀变速直线运动的推论
请大家自己证明!
1.在匀变速直线运动中,某段时间中间时刻的瞬时速度与该段的平均速度有什么样的关系?
2.在匀变速直线运动中,某段位移中间位置的瞬时速度与这段位移的初、末速度有什么样的关系?
匀变速直线运动的推论
你能比较
的大小吗?
3.在匀变速直线运动中连续相等的时间(T)内位移之差是恒量。
1 一个做匀减速直线运动的物体,经3.0s速度减为零,若测出它在最后1.0 s内的位移是1.0 m.那么该物体在这3.0 s内的平均速度是( )
A.1.0 m/s B.3.0 m/s
C.5.0 m/s D.9.0 m/s
答案:B
2 一观察者站在第一节车厢前端,当列车从静止开始做匀加速运动时,下列说法正确的是( )
A.每节车厢末端经过观察者的速度之比是1∶ …
B.每节车厢末端经过观察者的时间之比是1∶3∶5…
C.在相等时间里经过观察者的车厢数之比是1∶3∶5…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3…
解析:利用上述匀变速直线运动的特点来解题,很容易选出正确答案为A、C
答案:AC
3 一小球以某一初速度沿光滑斜面匀减速上滑,到达顶端时速度为0,历时3s,位移9m,求其第1秒内的位移。( )
(用两种方法解)
解法一:基本公式求加速度a
解法二:能不能用推论呢?
0
1s
2s
3s
0
v0
5m
3m
1m
a
v
从左往右运动,是匀减速至0的运动,逆过来看呢?
初速度为0的匀加速直线运动
用推论,OK!
5m
4 一列火车由等长的车厢连接而成,车厢之间的间隙忽略不计,一人站在站台上与第一节车厢的最前端相齐。当列车由静止开始做匀加速直线运动时,测得第一节车厢通过他的时间为2s,则从第5节至第16节车厢通过他的时间为多少?
答案 4s
5 运行着的汽车制动后做匀减速直线滑行,经3.5 s停止,试问它在制动开始的第1 s内和最后一秒内通过的位移之比为多少?
答案:6∶1
求解匀变速直线运动问题常见方法
方 法 分析说明
一般公式法 一般公式法指速度公式、位移公式及推论三式.它们均是矢量式,使用时要注意方向性.一般以v0的方向为正方向,其余与正方向相同者为正,与正方向相反者取负
平均速度法 定义式 对任何性质的运动都适用,而 (v0+vt)只适用于匀变速直线运动
中间时刻速度法 利用“任一时间t中间时刻的瞬时速度等于这段时间t内的平均速度”即vt/2= ,适用于任何一个匀变速直线运动
比例法 对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的比例关系求解
逆向思维法 把运动过程的“末态”作为“初态”的反向研究问题的方法.一般用于末态已知的情况
图象法 应用v ?t图象,可把较复杂的问题转变为较为简单的数学问题解决
推论法(Δx=at2) 对一般的匀变速直线运动问题,若出现相等的时间间隔问题,应优先考虑用Δx=at2求解
练习1.一物体由静止沿光滑斜面匀加速下滑距离为l时,速度为v,当它的速度是v/2时,它沿斜面下滑的距离是( )
C
解析:由vt2-v02=2ax知C正确
知 v2=2ax1, 4v2-v2=2ax2, x1∶x2=1∶3.
解析: 由
练习2.一小球从A点由静止开始做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则AB∶BC等于( )
A.1∶1 B.1∶2 C.1∶3 D.1∶4
C
D
练习3.一物体从斜面顶端由静止开始匀加速下滑,经过斜面中点时速度为2 m/s,则物体到达斜面底端时的速度为( )
A.3 m/s B.4 m/s C.6 m/s D.
解析:
练习4.一小球沿斜面匀加速滑下,依次经过A?B?C三点.已知AB=6 cm,BC=10 cm,小球经过AB和BC两段所用的时间均为2 s,则小球经过A?B?C三点时的速度大小分别为
( )
A.2 cm/s,3 cm/s,4 cm/s
B.2 cm/s,4 cm/s,6 cm/s
C.3 cm/s,4 cm/s,5 cm/s
D.3 cm/s,5 cm/s,7 cm/s
B
C
练习5.一列火车由静止以恒定的加速度启动出站,设每节车厢的长度相同,不计车厢间的间隙距离,一观察者站在第一节车厢的最前端,他通过测时间估算出第一节车厢尾驶过他时的速度为v0,则第n节车厢尾驶过他时的速度为
( )
解析:
匀变速直线运动规律的应用
思考:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,他运动的加速度大小为多少?
?
一、推导公式:速度与位移的关系
式中四个量都是矢量,都有正负
不涉及到时间t,用这个公式方便
例题:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,他运动的加速度大小为多少?通过这段山坡需用多长时间?
练习1.某飞机着陆时的速度为216km/h,随后匀减速滑行,加速度大小是2m/s2,机场跑道至少要多少米飞机才能安全着陆?
练习2.通过测试得知某型号的卡车在某种路面上急刹车时加速度大小是5m/s2。如果要求它在这种路面上行驶时在22.5m内必须停下,它的行驶速度不能超过多少?
思考:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,通过这段山坡需用多长时间?
?
V
0
t
t
V0
vt
又因为
此公式只适应于匀变速直线运动
二、补充公式:
——匀变速直线运动的平均速度公式
不涉及加速度a
例题:一个高山滑雪的人,从100 m长的山坡上匀加速滑下,初速度为5 m/s,末速度为15 m/s,通过这段山坡需用多长时间?
练习:骑自行车的人原来的速度是3m/s,下坡时做匀加速直线运动,通过50m的坡路后速度达到5m/s,求下坡所用时间和加速度的大小。
五个基本公式
加速度公式
速度公式
位移公式
速度与位移公式
平均速度公式
(1)1s末、2s末、 3s末……ns末的速度之比为多少?
(2)1s内、2s内、 3s内……ns内的位移之比为多少?
(3)第1s内、第2s内、第 3s内……第ns内的位移之比为多少?
(4)第1个x、第2个x、第 3个x……第n个x相邻相等位移的时间之比为多少?
1:2:3:…:n
1:4:9:…:n2
1:3:5:…:2n-1
三、 初速度为0的匀变速直线运动的推论
请大家自己证明!
1.在匀变速直线运动中,某段时间中间时刻的瞬时速度与该段的平均速度有什么样的关系?
2.在匀变速直线运动中,某段位移中间位置的瞬时速度与这段位移的初、末速度有什么样的关系?
匀变速直线运动的推论
你能比较
的大小吗?
3.在匀变速直线运动中连续相等的时间(T)内位移之差是恒量。
1 一个做匀减速直线运动的物体,经3.0s速度减为零,若测出它在最后1.0 s内的位移是1.0 m.那么该物体在这3.0 s内的平均速度是( )
A.1.0 m/s B.3.0 m/s
C.5.0 m/s D.9.0 m/s
答案:B
2 一观察者站在第一节车厢前端,当列车从静止开始做匀加速运动时,下列说法正确的是( )
A.每节车厢末端经过观察者的速度之比是1∶ …
B.每节车厢末端经过观察者的时间之比是1∶3∶5…
C.在相等时间里经过观察者的车厢数之比是1∶3∶5…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3…
解析:利用上述匀变速直线运动的特点来解题,很容易选出正确答案为A、C
答案:AC
3 一小球以某一初速度沿光滑斜面匀减速上滑,到达顶端时速度为0,历时3s,位移9m,求其第1秒内的位移。( )
(用两种方法解)
解法一:基本公式求加速度a
解法二:能不能用推论呢?
0
1s
2s
3s
0
v0
5m
3m
1m
a
v
从左往右运动,是匀减速至0的运动,逆过来看呢?
初速度为0的匀加速直线运动
用推论,OK!
5m
4 一列火车由等长的车厢连接而成,车厢之间的间隙忽略不计,一人站在站台上与第一节车厢的最前端相齐。当列车由静止开始做匀加速直线运动时,测得第一节车厢通过他的时间为2s,则从第5节至第16节车厢通过他的时间为多少?
答案 4s
5 运行着的汽车制动后做匀减速直线滑行,经3.5 s停止,试问它在制动开始的第1 s内和最后一秒内通过的位移之比为多少?
答案:6∶1
求解匀变速直线运动问题常见方法
方 法 分析说明
一般公式法 一般公式法指速度公式、位移公式及推论三式.它们均是矢量式,使用时要注意方向性.一般以v0的方向为正方向,其余与正方向相同者为正,与正方向相反者取负
平均速度法 定义式 对任何性质的运动都适用,而 (v0+vt)只适用于匀变速直线运动
中间时刻速度法 利用“任一时间t中间时刻的瞬时速度等于这段时间t内的平均速度”即vt/2= ,适用于任何一个匀变速直线运动
比例法 对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的比例关系求解
逆向思维法 把运动过程的“末态”作为“初态”的反向研究问题的方法.一般用于末态已知的情况
图象法 应用v ?t图象,可把较复杂的问题转变为较为简单的数学问题解决
推论法(Δx=at2) 对一般的匀变速直线运动问题,若出现相等的时间间隔问题,应优先考虑用Δx=at2求解
练习1.一物体由静止沿光滑斜面匀加速下滑距离为l时,速度为v,当它的速度是v/2时,它沿斜面下滑的距离是( )
C
解析:由vt2-v02=2ax知C正确
知 v2=2ax1, 4v2-v2=2ax2, x1∶x2=1∶3.
解析: 由
练习2.一小球从A点由静止开始做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则AB∶BC等于( )
A.1∶1 B.1∶2 C.1∶3 D.1∶4
C
D
练习3.一物体从斜面顶端由静止开始匀加速下滑,经过斜面中点时速度为2 m/s,则物体到达斜面底端时的速度为( )
A.3 m/s B.4 m/s C.6 m/s D.
解析:
练习4.一小球沿斜面匀加速滑下,依次经过A?B?C三点.已知AB=6 cm,BC=10 cm,小球经过AB和BC两段所用的时间均为2 s,则小球经过A?B?C三点时的速度大小分别为
( )
A.2 cm/s,3 cm/s,4 cm/s
B.2 cm/s,4 cm/s,6 cm/s
C.3 cm/s,4 cm/s,5 cm/s
D.3 cm/s,5 cm/s,7 cm/s
B
C
练习5.一列火车由静止以恒定的加速度启动出站,设每节车厢的长度相同,不计车厢间的间隙距离,一观察者站在第一节车厢的最前端,他通过测时间估算出第一节车厢尾驶过他时的速度为v0,则第n节车厢尾驶过他时的速度为
( )
解析:
同课章节目录
- 开篇 激动人心的万千体验
- 01物理学——理性的追求
- 02物理学——人类文明的奇葩
- 03学物理——探究求真
- 第一章 怎样描述物体的运动
- 1 走近运动
- 2 怎样描述运动的快慢
- 3 怎样描述运动的快慢(续)
- 4 怎样描述速度变化的快慢
- 第二章 研究匀变速直线运动的规律
- 1 伽利略对落体运动的研究
- 2 自由落体运动的规律
- 3 匀变速直线运动的规律
- 4 匀变速直线运动规律的应用
- 第三章 力与相互作用
- 1 牛顿第三定律
- 2 弹力
- 3 摩擦力
- 4 分析物体的受力
- 第四章 怎样求合力与分力
- 1 怎样求合力
- 2 怎样分解力
- 3 共点力的平衡及其应用
- 第五章 研究力和运动的关系
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿运动定律的案例分析
- 5 超重与失重
