2019-2020学年上海市松江区九年级(上)期中数学试卷试题(解析版)
文档属性
| 名称 | 2019-2020学年上海市松江区九年级(上)期中数学试卷试题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-13 00:00:00 | ||
图片预览

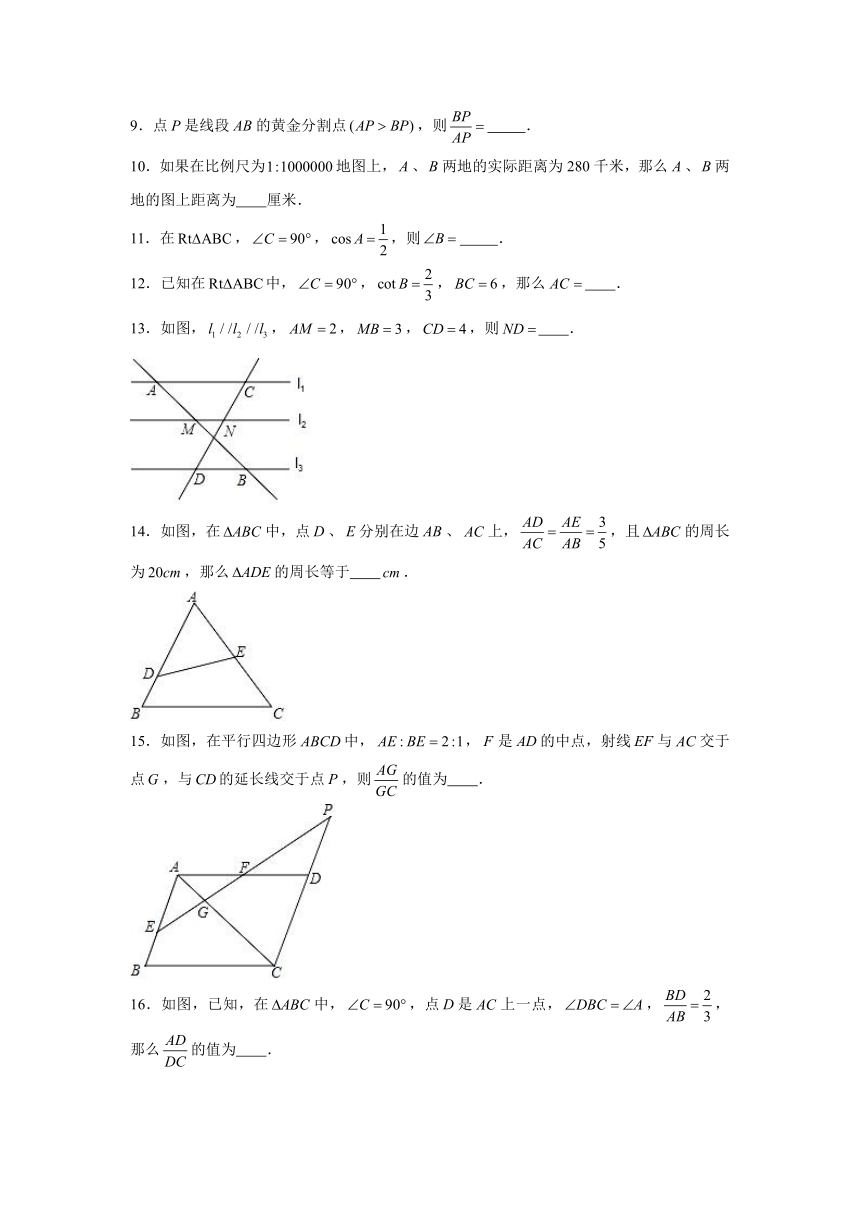


文档简介
2019-2020学年上海市松江区九年级(上)期中数学试卷
一、选择题(每题4分,共24分)
1.若两个相似三角形的周长之比是,那么这两个三角形的面积之比是
A. B. C. D.
2.已知中,,,,那么的值
A. B. C. D.
3.已知,下列结论中,错误的是
A. B.
C. D.
4.已知、是两个非零向量,且,下列结论:①;②;③;④与同向,其中正确的有几个
A.1 B.2 C.3 D.4
5.已知,在中,点、分别在边、上,,,那么下列各条件中,不一定能判定的是
A. B. C. D.
6.如图,在等腰中,,是边上的高,,则与的面积比是
A. B. C. D.
二、填空题(每题4分,共48分)
7.如果,那么 .
8.已知线段,,那么线段和的比例中项为 .
9.点是线段的黄金分割点,则 .
10.如果在比例尺为地图上,、两地的实际距离为280千米,那么、两地的图上距离为 厘米.
11.在,,,则 .
12.已知在中,,,,那么 .
13.如图,,,,,则 .
14.如图,在中,点、分别在边、上,,且的周长为,那么的周长等于 .
15.如图,在平行四边形中,,是的中点,射线与交于点,与的延长线交于点,则的值为 .
16.如图,已知,在中,,点是上一点,,,那么的值为 .
17.如图,在中,点是两条中线、的交点,设,,如果用,表示,那么 .
18.在中,,是边的中点,如果将绕着点旋转至△的位置,当落在边上时,,联结,则的正切值等于 .
三、解答题(本大题共7题,满分78分)
19.
20.已知:如图,两个不平行的向量和.先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
21.如图,在中,点、分别在边、上,、交于点,,.
(1)如果,求的长;
(2)如果的面积为1,求的面积.
22.如图,在梯形中,,,,,.
(1)求的长;
(2)求的值.
23.已知:如图,在等腰中,,是延长线上的一点,点是的中点,,,与交于点.
(1)求证:;
(2)求证:.
24.如图,已知等腰中,,,与轴交于点,,.
(1)求点的坐标;
(2)求的长;
(3)探究:在轴上是否存在点,使以、、为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
25.如图,在矩形中,是对角线的中点,,,点是射线上的一个动点,点在射线上,且满足,过点作,交射线于点.
(1)求证:.
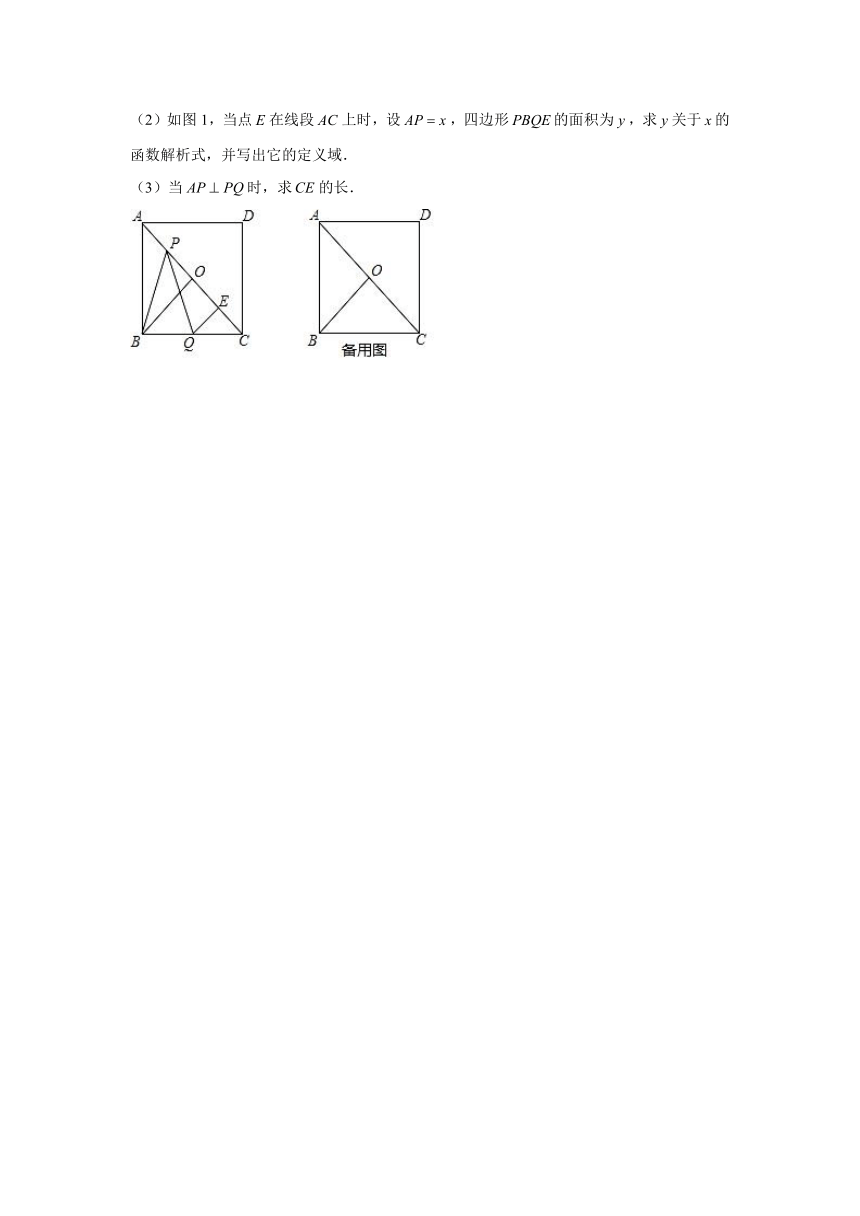
(2)如图1,当点在线段上时,设,四边形的面积为,求关于的函数解析式,并写出它的定义域.
(3)当时,求的长.
2019-2020学年上海市松江区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题4分,共24分)
1.若两个相似三角形的周长之比是,那么这两个三角形的面积之比是
A. B. C. D.
【解答】解:相似三角形的周长之比是,
对应边之比为,
这两个三角形的面积之比是:,
故选:.
2.已知中,,,,那么的值
A. B. C. D.
【解答】解:如图所示:
在中,,,,
.
故选:.
3.已知,下列结论中,错误的是
A. B.
C. D.
【解答】解:,
,,,
所以正确,错误.
故选:.
4.已知、是两个非零向量,且,下列结论:①;②;③;④与同向,其中正确的有几个
A.1 B.2 C.3 D.4
【解答】解:、是两个非零向量,且,
;;,
与方向相反,
故①②③正确,④错误,
故选:.
5.已知,在中,点、分别在边、上,,,那么下列各条件中,不一定能判定的是
A. B. C. D.
【解答】解:,,
,
,
,,,
而得不出,
故选:.
6.如图,在等腰中,,是边上的高,,则与的面积比是
A. B. C. D.
【解答】解:作于,
,
,
在中,,
,
,
在中,,
,
,
,
,
故选:.
二、填空题(每题4分,共48分)
7.如果,那么 .
【解答】解:把代入得.
故答案为.
8.已知线段,,那么线段和的比例中项为 4 .
【解答】解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是,则,(线段是正数,负值舍去).
故答案为4.
9.点是线段的黄金分割点,则 .
【解答】解:点是线段的黄金分割点,
.
故答案为.
10.如果在比例尺为地图上,、两地的实际距离为280千米,那么、两地的图上距离为 28 厘米.
【解答】解:设、两地的实际距离是厘米,
比例尺为,、两地的实际距离为280千米,
、两地的图上距离厘米.
故答案为28.
11.在,,,则 .
【解答】解:,,
,
则.
故答案为:.
12.已知在中,,,,那么 9 .
【解答】解:,
.
故答案是:9.
13.如图,,,,,则 .
【解答】解:,
,
即,
解得:,
故答案为:.
14.如图,在中,点、分别在边、上,,且的周长为,那么的周长等于 12 .
【解答】解:,,
,
,
的周长为,
的周长为.
故答案为12.
15.如图,在平行四边形中,,是的中点,射线与交于点,与的延长线交于点,则的值为 .
【解答】解:四边形是平行四边形,
,,
,
,,
,
,
,设,,
,,
,
,
故答案为.
16.如图,已知,在中,,点是上一点,,,那么的值为 .
【解答】解:在和中
,
设,,
则
故答案为:.
17.如图,在中,点是两条中线、的交点,设,,如果用,表示,那么 .
【解答】解:连接.
,,
,,
,
,
,
,,,
,
,
故答案为.
18.在中,,是边的中点,如果将绕着点旋转至△的位置,当落在边上时,,联结,则的正切值等于 .
【解答】解:如图,是边的中点,
,
如果将绕着点旋转至△的位置,当落在边上,
,,,
,
,
是等腰直角三角形,
,
,
是等腰直角三角形,
,
延长交于,延长交于,
则四边形是正方形,,
,,,
,
,
设,则,
,
的正切值,
故答案为:.
三、解答题(本大题共7题,满分78分)
19.
【解答】解:原式,
,
.
20.已知:如图,两个不平行的向量和.先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
【解答】解:.
如图即为所求.
21.如图,在中,点、分别在边、上,、交于点,,.
(1)如果,求的长;
(2)如果的面积为1,求的面积.
【解答】解:(1),,
,
,
,,
,,
.
(2),
,
.
22.如图,在梯形中,,,,,.
(1)求的长;
(2)求的值.
【解答】解:(1)作于,如图1所示:
则四边形是矩形,
,,
,
设,则,
,
解得:,
,,;
(2)作于,如图2所示:
,,
,
的面积,
,
.
23.已知:如图,在等腰中,,是延长线上的一点,点是的中点,,,与交于点.
(1)求证:;
(2)求证:.
【解答】(1)证明:点是的中点,,,
,;,
,
,
,
;
(2)证明:
又
.
24.如图,已知等腰中,,,与轴交于点,,.
(1)求点的坐标;
(2)求的长;
(3)探究:在轴上是否存在点,使以、、为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
【解答】解:(1)如图1,
过点作轴于,
,,
,,
,
,
,
,
,
,
,
,
;
(2)如图2,由(2)知,,
,
,
,,
,
过点作轴于,过点作轴于,
由(1)知,,
由(2)知,,
,
,
在中,,
,
;
(3)由(2)知,,,,,
由(1)知,,
,
以、、为顶点的三角形与相似,
①当时,
,
,
,
,
,,
②当时,
,
,
,
,
,
即:满足条件的点的坐标为,或.
25.如图,在矩形中,是对角线的中点,,,点是射线上的一个动点,点在射线上,且满足,过点作,交射线于点.
(1)求证:.
(2)如图1,当点在线段上时,设,四边形的面积为,求关于的函数解析式,并写出它的定义域.
(3)当时,求的长.
【解答】证明:(1)是斜边的中线,
,
,
,
,
又,,
,
,
,且,,
,
;
(2),,
,
,
设,则,
由(1)知:
,
,
,
,
,
设边上的高为,
,
,
.
(3)如图2,过点作,交于点,
,,
,
,,,,
,
,
,
设,
,
设,,
,
,
,
,
或(舍去)
,
,
,
,
.
一、选择题(每题4分,共24分)
1.若两个相似三角形的周长之比是,那么这两个三角形的面积之比是
A. B. C. D.
2.已知中,,,,那么的值
A. B. C. D.
3.已知,下列结论中,错误的是
A. B.
C. D.
4.已知、是两个非零向量,且,下列结论:①;②;③;④与同向,其中正确的有几个
A.1 B.2 C.3 D.4
5.已知,在中,点、分别在边、上,,,那么下列各条件中,不一定能判定的是
A. B. C. D.
6.如图,在等腰中,,是边上的高,,则与的面积比是
A. B. C. D.
二、填空题(每题4分,共48分)
7.如果,那么 .
8.已知线段,,那么线段和的比例中项为 .
9.点是线段的黄金分割点,则 .
10.如果在比例尺为地图上,、两地的实际距离为280千米,那么、两地的图上距离为 厘米.
11.在,,,则 .
12.已知在中,,,,那么 .
13.如图,,,,,则 .
14.如图,在中,点、分别在边、上,,且的周长为,那么的周长等于 .
15.如图,在平行四边形中,,是的中点,射线与交于点,与的延长线交于点,则的值为 .
16.如图,已知,在中,,点是上一点,,,那么的值为 .
17.如图,在中,点是两条中线、的交点,设,,如果用,表示,那么 .
18.在中,,是边的中点,如果将绕着点旋转至△的位置,当落在边上时,,联结,则的正切值等于 .
三、解答题(本大题共7题,满分78分)
19.
20.已知:如图,两个不平行的向量和.先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
21.如图,在中,点、分别在边、上,、交于点,,.
(1)如果,求的长;
(2)如果的面积为1,求的面积.
22.如图,在梯形中,,,,,.
(1)求的长;
(2)求的值.
23.已知:如图,在等腰中,,是延长线上的一点,点是的中点,,,与交于点.
(1)求证:;
(2)求证:.
24.如图,已知等腰中,,,与轴交于点,,.
(1)求点的坐标;
(2)求的长;
(3)探究:在轴上是否存在点,使以、、为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
25.如图,在矩形中,是对角线的中点,,,点是射线上的一个动点,点在射线上,且满足,过点作,交射线于点.
(1)求证:.
(2)如图1,当点在线段上时,设,四边形的面积为,求关于的函数解析式,并写出它的定义域.
(3)当时,求的长.
2019-2020学年上海市松江区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题4分,共24分)
1.若两个相似三角形的周长之比是,那么这两个三角形的面积之比是
A. B. C. D.
【解答】解:相似三角形的周长之比是,
对应边之比为,
这两个三角形的面积之比是:,
故选:.
2.已知中,,,,那么的值
A. B. C. D.
【解答】解:如图所示:
在中,,,,
.
故选:.
3.已知,下列结论中,错误的是
A. B.
C. D.
【解答】解:,
,,,
所以正确,错误.
故选:.
4.已知、是两个非零向量,且,下列结论:①;②;③;④与同向,其中正确的有几个
A.1 B.2 C.3 D.4
【解答】解:、是两个非零向量,且,
;;,
与方向相反,
故①②③正确,④错误,
故选:.
5.已知,在中,点、分别在边、上,,,那么下列各条件中,不一定能判定的是
A. B. C. D.
【解答】解:,,
,
,
,,,
而得不出,
故选:.
6.如图,在等腰中,,是边上的高,,则与的面积比是
A. B. C. D.
【解答】解:作于,
,
,
在中,,
,
,
在中,,
,
,
,
,
故选:.
二、填空题(每题4分,共48分)
7.如果,那么 .
【解答】解:把代入得.
故答案为.
8.已知线段,,那么线段和的比例中项为 4 .
【解答】解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是,则,(线段是正数,负值舍去).
故答案为4.
9.点是线段的黄金分割点,则 .
【解答】解:点是线段的黄金分割点,
.
故答案为.
10.如果在比例尺为地图上,、两地的实际距离为280千米,那么、两地的图上距离为 28 厘米.
【解答】解:设、两地的实际距离是厘米,
比例尺为,、两地的实际距离为280千米,
、两地的图上距离厘米.
故答案为28.
11.在,,,则 .
【解答】解:,,
,
则.
故答案为:.
12.已知在中,,,,那么 9 .
【解答】解:,
.
故答案是:9.
13.如图,,,,,则 .
【解答】解:,
,
即,
解得:,
故答案为:.
14.如图,在中,点、分别在边、上,,且的周长为,那么的周长等于 12 .
【解答】解:,,
,
,
的周长为,
的周长为.
故答案为12.
15.如图,在平行四边形中,,是的中点,射线与交于点,与的延长线交于点,则的值为 .
【解答】解:四边形是平行四边形,
,,
,
,,
,
,
,设,,
,,
,
,
故答案为.
16.如图,已知,在中,,点是上一点,,,那么的值为 .
【解答】解:在和中
,
设,,
则
故答案为:.
17.如图,在中,点是两条中线、的交点,设,,如果用,表示,那么 .
【解答】解:连接.
,,
,,
,
,
,
,,,
,
,
故答案为.
18.在中,,是边的中点,如果将绕着点旋转至△的位置,当落在边上时,,联结,则的正切值等于 .
【解答】解:如图,是边的中点,
,
如果将绕着点旋转至△的位置,当落在边上,
,,,
,
,
是等腰直角三角形,
,
,
是等腰直角三角形,
,
延长交于,延长交于,
则四边形是正方形,,
,,,
,
,
设,则,
,
的正切值,
故答案为:.
三、解答题(本大题共7题,满分78分)
19.
【解答】解:原式,
,
.
20.已知:如图,两个不平行的向量和.先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
【解答】解:.
如图即为所求.
21.如图,在中,点、分别在边、上,、交于点,,.
(1)如果,求的长;
(2)如果的面积为1,求的面积.
【解答】解:(1),,
,
,
,,
,,
.
(2),
,
.
22.如图,在梯形中,,,,,.
(1)求的长;
(2)求的值.
【解答】解:(1)作于,如图1所示:
则四边形是矩形,
,,
,
设,则,
,
解得:,
,,;
(2)作于,如图2所示:
,,
,
的面积,
,
.
23.已知:如图,在等腰中,,是延长线上的一点,点是的中点,,,与交于点.
(1)求证:;
(2)求证:.
【解答】(1)证明:点是的中点,,,
,;,
,
,
,
;
(2)证明:
又
.
24.如图,已知等腰中,,,与轴交于点,,.
(1)求点的坐标;
(2)求的长;
(3)探究:在轴上是否存在点,使以、、为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
【解答】解:(1)如图1,
过点作轴于,
,,
,,
,
,
,
,
,
,
,
,
;
(2)如图2,由(2)知,,
,
,
,,
,
过点作轴于,过点作轴于,
由(1)知,,
由(2)知,,
,
,
在中,,
,
;
(3)由(2)知,,,,,
由(1)知,,
,
以、、为顶点的三角形与相似,
①当时,
,
,
,
,
,,
②当时,
,
,
,
,
,
即:满足条件的点的坐标为,或.
25.如图,在矩形中,是对角线的中点,,,点是射线上的一个动点,点在射线上,且满足,过点作,交射线于点.
(1)求证:.
(2)如图1,当点在线段上时,设,四边形的面积为,求关于的函数解析式,并写出它的定义域.
(3)当时,求的长.
【解答】证明:(1)是斜边的中线,
,
,
,
,
又,,
,
,
,且,,
,
;
(2),,
,
,
设,则,
由(1)知:
,
,
,
,
,
设边上的高为,
,
,
.
(3)如图2,过点作,交于点,
,,
,
,,,,
,
,
,
设,
,
设,,
,
,
,
,
或(舍去)
,
,
,
,
.
同课章节目录
