人教高中数学必修四1.5函数y=Asin(wx b)的图像 课件(共23张PPT)
文档属性
| 名称 | 人教高中数学必修四1.5函数y=Asin(wx b)的图像 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 14:32:47 | ||
图片预览






文档简介
(共23张PPT)
函数y=Asin(ωx+φ)的图象
问题1:在函数y=Asin(ωx+φ)中A的作用,ω的作用?
学习反馈--复习巩固
在实际生活中,经常会遇到形如y=Asin(?x+?) (A>0, ?>0)函数
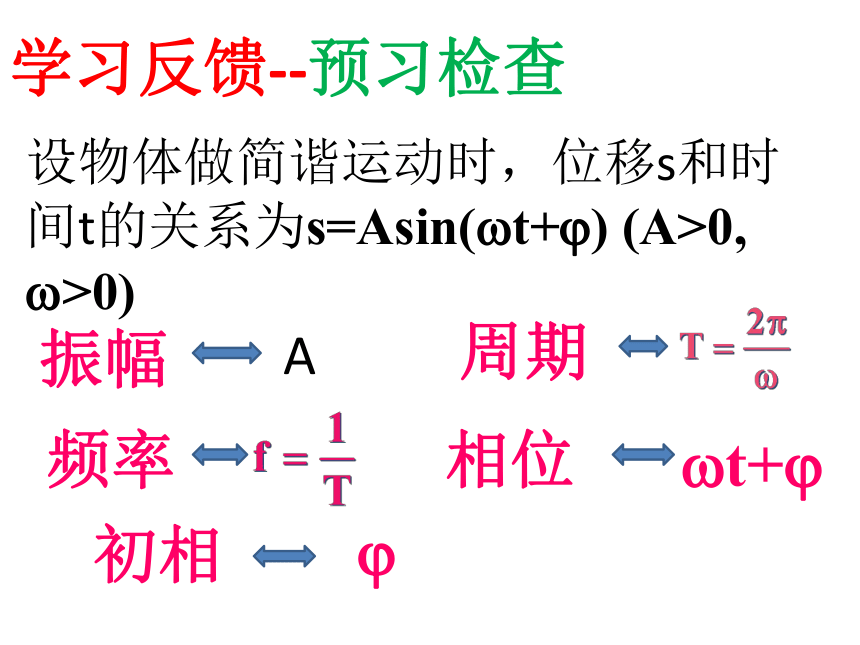
振幅
A
周期
频率
相位
?t+?
初相
?
学习反馈--预习检查
设物体做简谐运动时,位移s和时间t的关系为s=Asin(?t+?) (A>0, ?>0)
问题导学1
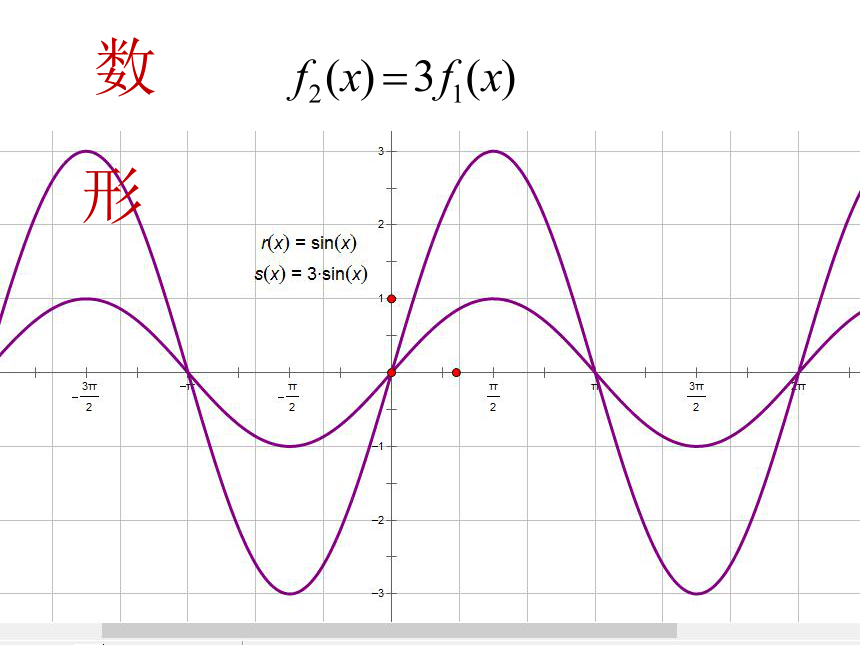
问题2:函数y=sinx的图像与函数y=3sinx的图像有什么关系
数
形
交流提升1
问题3:给出函数y=sinx的图像与函数y=Asinx (A >0且A≠1)的图像的关系
问题导学2
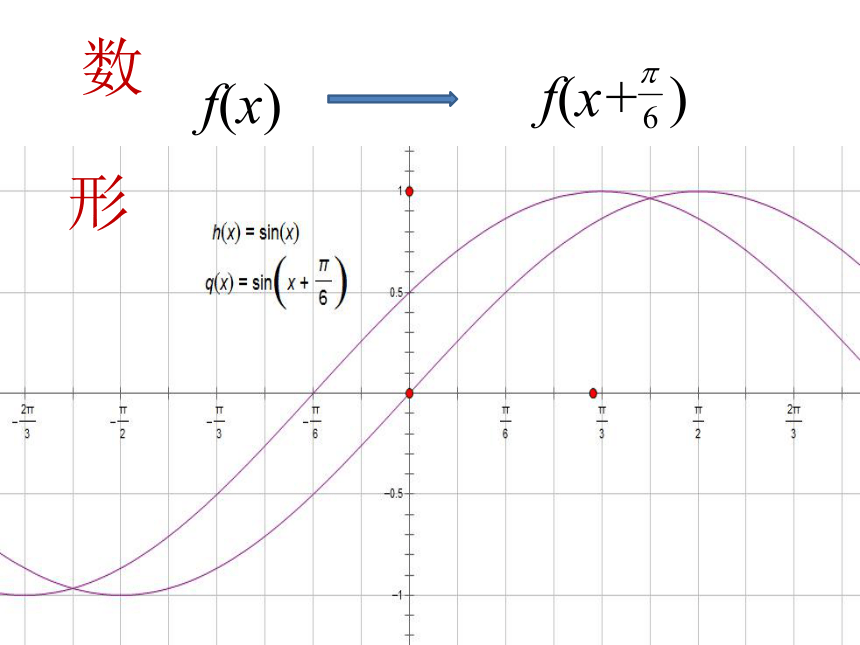
问题4:函数y=sinx的图像与函数y=sin(x+ )的图像有什么关系
f(x)
数
f(x+ )
形
交流提升2
问题5:给出函数y=sinx的图像与函数y=sin(x+φ)的图像的关系
问题6:函数y=sinx的图像与函数y=sin2x的图像有什么关系
f(x)
f ( )
数
2x
=sinx
x 2x即x
=sin2x
形
交流提升3
问题7:给出函数y=sinx的图像与函数y=sin?x (? >0且?≠1)的图像的关系
问题8:设函数y=sin2x的图像与函数y=sin(2x+ )的图像有什么关系
f(x)
f ( )
数
=sin2x
=sin(2x+ )
形
交流提升4
问题9:给出函数y=sinωx的图像与函数y=sin(ωx+φ) 的图像的关系
交流提升--训练反馈
解:
y=sinx
横坐标变为原来的
纵坐标不变
y=sin2x
纵坐标变为原来的3倍
横坐标不变
方法2
方法3
向右平移
?
y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:
y=sinx
向左(?>0)或向右(?<0)
平移???个单位
y=sin(x+?)
横坐标变为原来的 倍
纵坐标不变
1
?
y=sin(?x+?)
纵坐标变为原来的A倍
横坐标不变
y=Asin(?x+?)
?
或:
y=sinx
y=sin?x
横坐标变为原来的 倍
纵坐标不变
1
?
纵坐标变为原来的A倍
横坐标不变
y=Asin(?x+?)
向左(?>0)或向右(?<0)
平移? ?个单位
?
?
y=sin?(x+ )
?
?
=sin(?x+?)
总结延伸
1、要得到函数 的图象,只需将函数 的图象 ( )
A.向左平移个 单位 B.向右平移个 单位
C.向左平移个 单位 D.向右平移个 单位
D
2、将函数f(x)=sinx的横坐标伸长为原来的2倍,再向左平移 个单位所得的曲线是g(x)的图象,试求g(x)的解析式.
总结延伸
由解析式作图:
由函数y=Asin(?x+?)+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
总结反思
函数y=Asin(ωx+φ)的图象
问题1:在函数y=Asin(ωx+φ)中A的作用,ω的作用?
学习反馈--复习巩固
在实际生活中,经常会遇到形如y=Asin(?x+?) (A>0, ?>0)函数
振幅
A
周期
频率
相位
?t+?
初相
?
学习反馈--预习检查
设物体做简谐运动时,位移s和时间t的关系为s=Asin(?t+?) (A>0, ?>0)
问题导学1
问题2:函数y=sinx的图像与函数y=3sinx的图像有什么关系
数
形
交流提升1
问题3:给出函数y=sinx的图像与函数y=Asinx (A >0且A≠1)的图像的关系
问题导学2
问题4:函数y=sinx的图像与函数y=sin(x+ )的图像有什么关系
f(x)
数
f(x+ )
形
交流提升2
问题5:给出函数y=sinx的图像与函数y=sin(x+φ)的图像的关系
问题6:函数y=sinx的图像与函数y=sin2x的图像有什么关系
f(x)
f ( )
数
2x
=sinx
x 2x即x
=sin2x
形
交流提升3
问题7:给出函数y=sinx的图像与函数y=sin?x (? >0且?≠1)的图像的关系
问题8:设函数y=sin2x的图像与函数y=sin(2x+ )的图像有什么关系
f(x)
f ( )
数
=sin2x
=sin(2x+ )
形
交流提升4
问题9:给出函数y=sinωx的图像与函数y=sin(ωx+φ) 的图像的关系
交流提升--训练反馈
解:
y=sinx
横坐标变为原来的
纵坐标不变
y=sin2x
纵坐标变为原来的3倍
横坐标不变
方法2
方法3
向右平移
?
y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:
y=sinx
向左(?>0)或向右(?<0)
平移???个单位
y=sin(x+?)
横坐标变为原来的 倍
纵坐标不变
1
?
y=sin(?x+?)
纵坐标变为原来的A倍
横坐标不变
y=Asin(?x+?)
?
或:
y=sinx
y=sin?x
横坐标变为原来的 倍
纵坐标不变
1
?
纵坐标变为原来的A倍
横坐标不变
y=Asin(?x+?)
向左(?>0)或向右(?<0)
平移? ?个单位
?
?
y=sin?(x+ )
?
?
=sin(?x+?)
总结延伸
1、要得到函数 的图象,只需将函数 的图象 ( )
A.向左平移个 单位 B.向右平移个 单位
C.向左平移个 单位 D.向右平移个 单位
D
2、将函数f(x)=sinx的横坐标伸长为原来的2倍,再向左平移 个单位所得的曲线是g(x)的图象,试求g(x)的解析式.
总结延伸
由解析式作图:
由函数y=Asin(?x+?)+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
总结反思
