新人教版数学六年级上册第八单元测试卷(含答案)
文档属性
| 名称 | 新人教版数学六年级上册第八单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 284.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-13 10:27:31 | ||
图片预览

文档简介
新人教版数学六年级上册第八单元测试卷
姓名: 班级: 得分:
题号
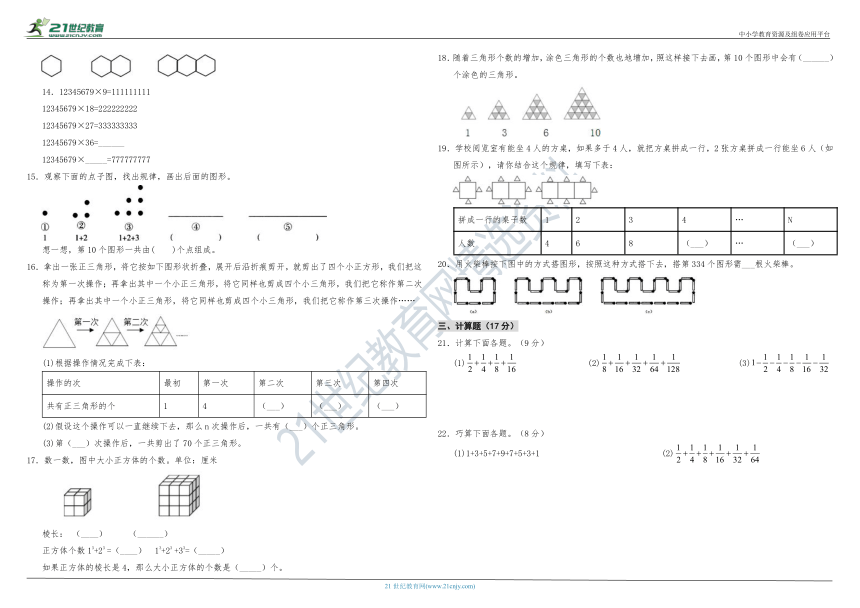
一
二
三
四
总分
得分
一、选择题(14分)
1.如下图,第8个点阵的点数是( )个。
A.36 B.35 C.32 D.28
2.,,,,…,则这一行数中的第10个数应该是( )。
A. B. C. D.
3.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是(??)。
A.86 B.32 C.158 D.74
4.笑笑用小棒以下面的方式摆六边形。
1个 2个 3个
摆n个六边形要用小棒( )根。
A.6n B.5n+1 C.4n+3
5.找规律:5,9,17,33,65,( )。
A.127 B.128 C.129 D.130
6.有一个从袋子中摸球的游戏,小红根据游戏规则,做出了如下图所示的树形图,则此次摸球的游戏规 则是(????)。
A.随机摸出一个球后放回,再随机摸出一个球
B.随机摸出一个球后不放回,再随机摸出一个球
C.随机摸出一个球后放回,再随机摸出三个球
D.随机摸出一个球后不放回,再随机摸出三个球
7.一组数据按下面顺序依次排列:1,3,2014,2,4,2012,3,5,2010,4,6,2008…第2016个数是 ( )
A.672 B.674 C.670 D.676
二、填空题(29分)
8.把边长为1厘米的正方形纸片,按下面的规律拼成长方形:
(1)用5个正方形拼成的长方形的周长是(_____)厘米;
(2)用n个正方形拼成的长方形的周长是(_____)厘米
9.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为 3,6,9,12.按这个规律由100个小等边三角形拼成的图形,周长为__________。
(1) (2) (3) (4)
10.观察下列图形中点的个数,若按其规律再画下去,可以得到第4个图形中所有点的个数为:_____, 第n个图形中所有点的个数为:_____。(用含n的式子表示)
图1 图2 图3
11.小明想要用棱长为1cm的小正方体搭建台阶(如图),他已搭建的台阶。分别有2cm,3cm 和4cm高。 如果小明一直这样搭下去,当用了105个方块时,他搭的台阶有_____cm高。
12.找规律填一填:3,5,9,17,_____,_____,129。
13.按下面的规律用小棒摆正六边形。摆4个正六边形需要_____根小棒;摆 n个正六边形需要_____根 小棒。
14.12345679×9=111111111
12345679×18=222222222
12345679×27=333333333
12345679×36=______
12345679×_____=777777777
15.观察下面的点子图,找出规律,画出后面的图形。
想一想,第10个图形一共由( )个点组成。
16.拿出一张正三角形,将它按如下图形状折叠,展开后沿折痕剪开,就剪出了四个小正方形,我们把这 称为第一次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第二次 操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第三次操作……
(1)根据操作情况完成下表:
操作的次
最初
第一次
第二次
第三次
第四次
共有正三角形的个
1
4
(___)
(___)
(___)
(2)假设这个操作可以一直继续下去,那么n次操作后,一共有(___)个正三角形。
(3)第(___)次操作后,一共剪出了70个正三角形。
17.数一数,图中大小正方体的个数。单位:厘米
棱长: (____) (______)
正方体个数13+23 =(____) 13+23 +33=(_____)
如果正方体的棱长是4,那么大小正方体的个数是(_____)个。
18.随着三角形个数的增加,涂色三角形的个数也地增加,照这样接下去画,第10个图形中会有(______) 个涂色的三角形。
19.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如 图所示),请你结合这个规律,填写下表:
拼成一行的桌子数
1
2
3
4
…
N
人数
4
6
8
(___)
…
(___)
20.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需___根火柴棒。
三、计算题(17分)
21.计算下面各题。(9分)
(1) (2) (3)
22.巧算下面各题。(8分)
(1)1+3+5+7+9+7+5+3+1 (2)
四、解答题(40分)
23.下图是杨辉三角,是以我国南宋数学家杨辉的名字来命名的,杨辉在其著作中对杨辉三角的详解比欧 洲帕斯卡三角要早393年。请你找出规律,再写出一行数字。
24.两个点可连一条线段,三个点可连3条线段,那么12个点可连多少条线段?14个点呢?写出推理过 程.
25.数一数。
(1)图中各有多少个▲和△?
序号
①
②
③
④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
26.龙一鸣、黄霏霏、苹苹、淘淘和依依5个好朋友聚会,每两人之间都要握一次手。已知龙一鸣已经握 了4次手,黄霏霏已经握了3次手,依依已经握了2次手,苹苹已经握了1次手。淘淘一共握了几次 手?分别与谁握的?(可画图连一连)
27.你能利用下面的图发现这一公式吗?利用你所学的面积计算的知识,探索一下。
参考答案
1.A
2.C
3.C
4.B
5.C
6.C
7.A
8.12 2n+2
9.30
10.25 (n+1)2
11.6
12.33 65
13.21 5n+1
14.444444444 63
15. 55
16.7 10 13 3n+1 23
17.2 3 9 36 100
18.55
19.10 2n+2
20.2010
21.(1);(2);(3)
22.(1)41;(2)
23.1,6,15,20,15,6,1
24.66 91
25.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
26.
由图可以看出淘淘一共握了两次手,分别是与龙一鸣和黄霏霏握的。
27.从图中可以看出:
=
=
姓名: 班级: 得分:
题号
一
二
三
四
总分
得分
一、选择题(14分)
1.如下图,第8个点阵的点数是( )个。
A.36 B.35 C.32 D.28
2.,,,,…,则这一行数中的第10个数应该是( )。
A. B. C. D.
3.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是(??)。
A.86 B.32 C.158 D.74
4.笑笑用小棒以下面的方式摆六边形。
1个 2个 3个
摆n个六边形要用小棒( )根。
A.6n B.5n+1 C.4n+3
5.找规律:5,9,17,33,65,( )。
A.127 B.128 C.129 D.130
6.有一个从袋子中摸球的游戏,小红根据游戏规则,做出了如下图所示的树形图,则此次摸球的游戏规 则是(????)。
A.随机摸出一个球后放回,再随机摸出一个球
B.随机摸出一个球后不放回,再随机摸出一个球
C.随机摸出一个球后放回,再随机摸出三个球
D.随机摸出一个球后不放回,再随机摸出三个球
7.一组数据按下面顺序依次排列:1,3,2014,2,4,2012,3,5,2010,4,6,2008…第2016个数是 ( )
A.672 B.674 C.670 D.676
二、填空题(29分)
8.把边长为1厘米的正方形纸片,按下面的规律拼成长方形:
(1)用5个正方形拼成的长方形的周长是(_____)厘米;
(2)用n个正方形拼成的长方形的周长是(_____)厘米
9.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为 3,6,9,12.按这个规律由100个小等边三角形拼成的图形,周长为__________。
(1) (2) (3) (4)
10.观察下列图形中点的个数,若按其规律再画下去,可以得到第4个图形中所有点的个数为:_____, 第n个图形中所有点的个数为:_____。(用含n的式子表示)
图1 图2 图3
11.小明想要用棱长为1cm的小正方体搭建台阶(如图),他已搭建的台阶。分别有2cm,3cm 和4cm高。 如果小明一直这样搭下去,当用了105个方块时,他搭的台阶有_____cm高。
12.找规律填一填:3,5,9,17,_____,_____,129。
13.按下面的规律用小棒摆正六边形。摆4个正六边形需要_____根小棒;摆 n个正六边形需要_____根 小棒。
14.12345679×9=111111111
12345679×18=222222222
12345679×27=333333333
12345679×36=______
12345679×_____=777777777
15.观察下面的点子图,找出规律,画出后面的图形。
想一想,第10个图形一共由( )个点组成。
16.拿出一张正三角形,将它按如下图形状折叠,展开后沿折痕剪开,就剪出了四个小正方形,我们把这 称为第一次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第二次 操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第三次操作……
(1)根据操作情况完成下表:
操作的次
最初
第一次
第二次
第三次
第四次
共有正三角形的个
1
4
(___)
(___)
(___)
(2)假设这个操作可以一直继续下去,那么n次操作后,一共有(___)个正三角形。
(3)第(___)次操作后,一共剪出了70个正三角形。
17.数一数,图中大小正方体的个数。单位:厘米
棱长: (____) (______)
正方体个数13+23 =(____) 13+23 +33=(_____)
如果正方体的棱长是4,那么大小正方体的个数是(_____)个。
18.随着三角形个数的增加,涂色三角形的个数也地增加,照这样接下去画,第10个图形中会有(______) 个涂色的三角形。
19.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如 图所示),请你结合这个规律,填写下表:
拼成一行的桌子数
1
2
3
4
…
N
人数
4
6
8
(___)
…
(___)
20.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需___根火柴棒。
三、计算题(17分)
21.计算下面各题。(9分)
(1) (2) (3)
22.巧算下面各题。(8分)
(1)1+3+5+7+9+7+5+3+1 (2)
四、解答题(40分)
23.下图是杨辉三角,是以我国南宋数学家杨辉的名字来命名的,杨辉在其著作中对杨辉三角的详解比欧 洲帕斯卡三角要早393年。请你找出规律,再写出一行数字。
24.两个点可连一条线段,三个点可连3条线段,那么12个点可连多少条线段?14个点呢?写出推理过 程.
25.数一数。
(1)图中各有多少个▲和△?
序号
①
②
③
④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
26.龙一鸣、黄霏霏、苹苹、淘淘和依依5个好朋友聚会,每两人之间都要握一次手。已知龙一鸣已经握 了4次手,黄霏霏已经握了3次手,依依已经握了2次手,苹苹已经握了1次手。淘淘一共握了几次 手?分别与谁握的?(可画图连一连)
27.你能利用下面的图发现这一公式吗?利用你所学的面积计算的知识,探索一下。
参考答案
1.A
2.C
3.C
4.B
5.C
6.C
7.A
8.12 2n+2
9.30
10.25 (n+1)2
11.6
12.33 65
13.21 5n+1
14.444444444 63
15. 55
16.7 10 13 3n+1 23
17.2 3 9 36 100
18.55
19.10 2n+2
20.2010
21.(1);(2);(3)
22.(1)41;(2)
23.1,6,15,20,15,6,1
24.66 91
25.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
26.
由图可以看出淘淘一共握了两次手,分别是与龙一鸣和黄霏霏握的。
27.从图中可以看出:
=
=
