北京课改版七上1.3 相反数和绝对值 课件(22张PPT)
文档属性
| 名称 | 北京课改版七上1.3 相反数和绝对值 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 00:00:00 | ||
图片预览





文档简介
课件22张PPT。第一章 有理数11.3 相反数和绝对值
复习:1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
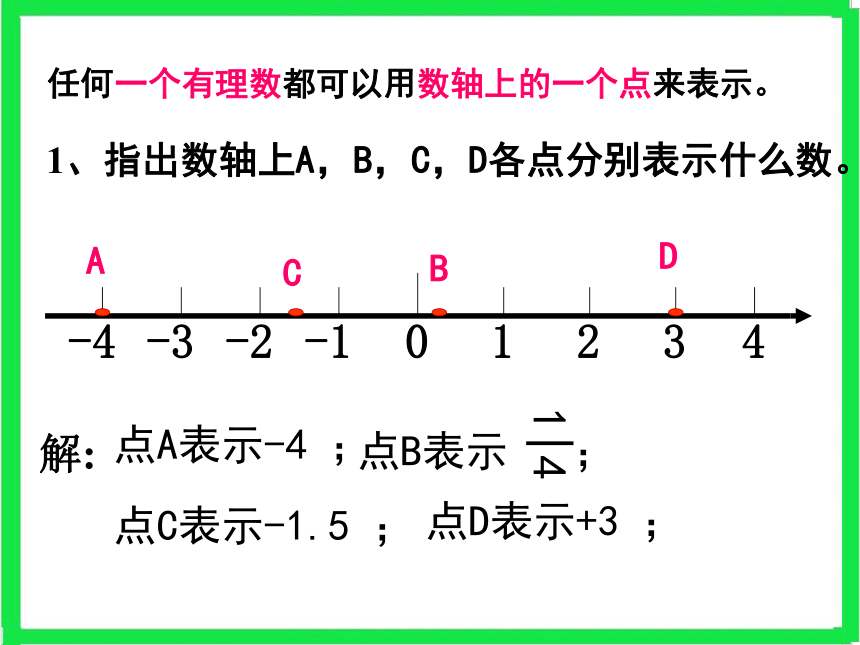
2、数轴的三要素原点、正方向、单位长度1、指出数轴上A,B,C,D各点分别表示什么数。0123-1-2-3-44A任何一个有理数都可以用数轴上的一个点来表示。BCD解:点A表示-4 ;点D表示+3 ;点C表示-1.5 ;解:例2画出数轴,并用数轴上的点表示下列各数:3|2-5,0,5,-4, 4-3|2,3|2- 505- 4任何一个有理数都可以用数轴上的一个点来表示。4+4与-4 如果两个数只有符号不同,那么我们称其中一个数
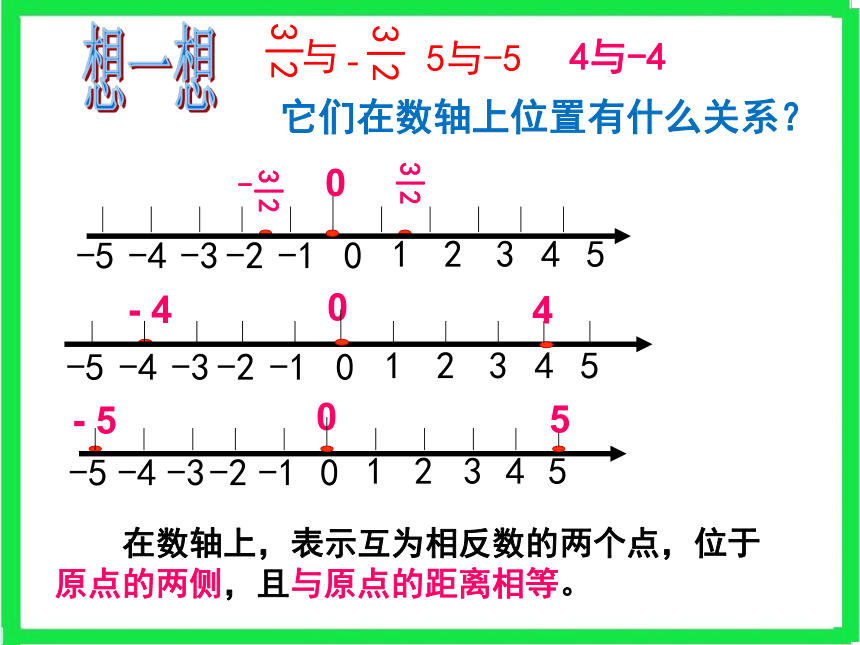
为另一个数的相反数,也称这两个数互为相反数。-5与+50的相反数是0。想一想:有什么相同点?想一想4与-4它们在数轴上位置有什么关系? 在数轴上,表示互为相反数的两个点,位于
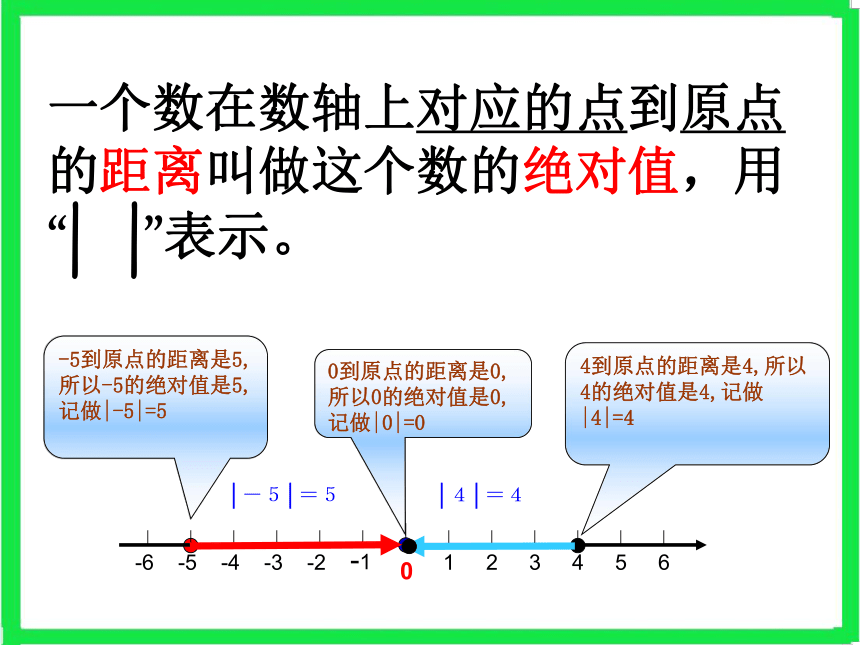
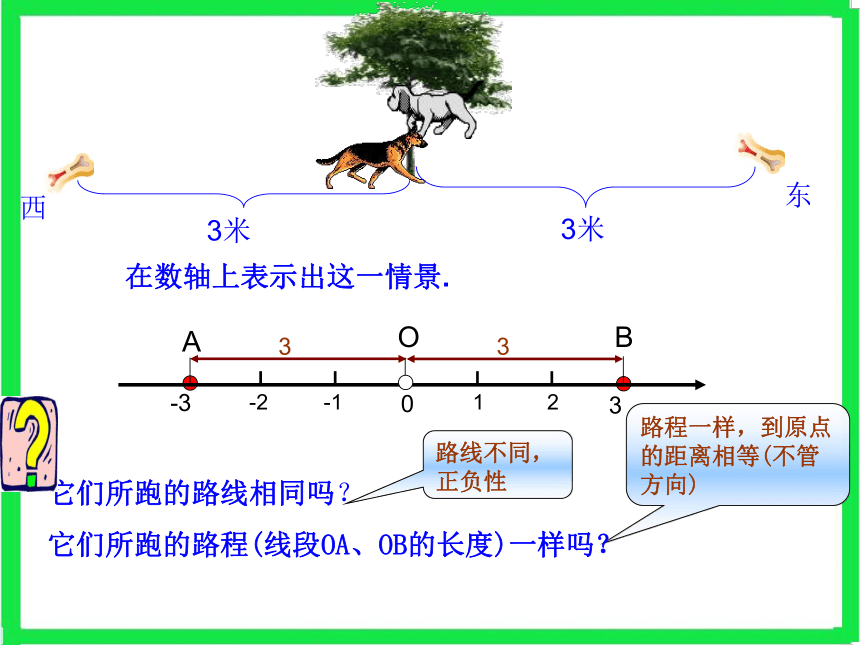
原点的两侧,且与原点的距离相等。│-5│=5│4│=44到原点的距离是4,所以4的绝对值是4,记做|4|=4-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示。0到原点的距离是0,所以0的绝对值是0,记做|0|=0西东33AOB3米3米路线不同,正负性路程一样,到原点的距离相等(不管方向) 它们所跑的路线相同吗?
它们所跑的路程(线段OA、OB的长度)一样吗? 在数轴上表示出这一情景.你发现了什么?求下列各组数的绝对值:想一想互为相反数的两个数的绝对值有什么关系? 解:(1)|4|=4 |-4|=4(2)|0.8|=0.8 |-0.8|=0.8解:|-21|21|0|0|-7.8|7.8====一个数的绝对值与这个数有什么关系? 议一议正数的绝对值是它本身负数的绝对值是它的相反数一个数的绝对值与这个数有什么关系? 议一议零的绝对值是零 (1)当a是正数时,|a|=____;(2)当a是负数时,|a|=__;(3)当a=0时,|a|=___。a-a0任何一个有理数的绝对值都是负数非!
1. 正数的绝对值是 ,负数的绝对值是 ,0的绝对值是 .
2. 6的相反数是( )
A.﹣6 B. C.﹣ D.6
3. 的相反数是( )
A.2 B.﹣2 C. D.﹣
它的本身它的相反数0AD小牛试刀:4. ﹣5的绝对值是( )
A. B.5 C.﹣ D.﹣5
5.如图,数轴上表示数﹣2的相反数的点是( )
A.点P B.点Q C.点M D.点N
BA(1). |-21|+|0|- |7|
(2)|-3| × |6.2|
我来试试计算:解:原式 = 21+0-7
= 14解:原式 = 3 × 6.2
= 18.6做一做 (1) 将- 1.5 , - 3 , - 1 ,- 5按从小到大的顺序排列。| -1.5 | = 1.5 ; | - 3 | = 3 | -1 | = 1 ; | - 5 | = 5.
(2) 求出- 1.5 , - 3 , - 1 , - 5的绝对值,并比较它们的大小。1 < 1.5 <3 <5-5 < -3 < -1.5 < -1 两个负数比较大小,绝对值大的反而小解法一(利用绝对值比较两个负数的大小)解: (1)| -1| = 1,| -5 | = 5 ,1﹤5,所以 - 1> - 5例题解法二 (利用数轴比较两个负数的大小)
(2)解:(1)因为- 5在 –1左边,所以 - 5﹤ - 1±422-67.220 老师,我来!比一比,看谁做得快又准!挑战自我01解:当|a|=0,|b-1|=0时, |a|+|b-1|=0
由|a|=0, 得a=0
|b-1|=0,即b-1=0, b=1已知|x-2|+|y- |=0,求2x+3y的值. 由|x-2|=0,得x=2
|y- |=0y=所以:2x+3y
=2 ×2 +3 ×
=5
挑战自我解:课时 小结:说一说,这节课你学到了什么?(1)绝对值的概念。(2)如何求一个数的绝对值。(3) 一个数的绝对值总是大于或等于0的。谢谢
复习:1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
2、数轴的三要素原点、正方向、单位长度1、指出数轴上A,B,C,D各点分别表示什么数。0123-1-2-3-44A任何一个有理数都可以用数轴上的一个点来表示。BCD解:点A表示-4 ;点D表示+3 ;点C表示-1.5 ;解:例2画出数轴,并用数轴上的点表示下列各数:3|2-5,0,5,-4, 4-3|2,3|2- 505- 4任何一个有理数都可以用数轴上的一个点来表示。4+4与-4 如果两个数只有符号不同,那么我们称其中一个数
为另一个数的相反数,也称这两个数互为相反数。-5与+50的相反数是0。想一想:有什么相同点?想一想4与-4它们在数轴上位置有什么关系? 在数轴上,表示互为相反数的两个点,位于
原点的两侧,且与原点的距离相等。│-5│=5│4│=44到原点的距离是4,所以4的绝对值是4,记做|4|=4-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示。0到原点的距离是0,所以0的绝对值是0,记做|0|=0西东33AOB3米3米路线不同,正负性路程一样,到原点的距离相等(不管方向) 它们所跑的路线相同吗?
它们所跑的路程(线段OA、OB的长度)一样吗? 在数轴上表示出这一情景.你发现了什么?求下列各组数的绝对值:想一想互为相反数的两个数的绝对值有什么关系? 解:(1)|4|=4 |-4|=4(2)|0.8|=0.8 |-0.8|=0.8解:|-21|21|0|0|-7.8|7.8====一个数的绝对值与这个数有什么关系? 议一议正数的绝对值是它本身负数的绝对值是它的相反数一个数的绝对值与这个数有什么关系? 议一议零的绝对值是零 (1)当a是正数时,|a|=____;(2)当a是负数时,|a|=__;(3)当a=0时,|a|=___。a-a0任何一个有理数的绝对值都是负数非!
1. 正数的绝对值是 ,负数的绝对值是 ,0的绝对值是 .
2. 6的相反数是( )
A.﹣6 B. C.﹣ D.6
3. 的相反数是( )
A.2 B.﹣2 C. D.﹣
它的本身它的相反数0AD小牛试刀:4. ﹣5的绝对值是( )
A. B.5 C.﹣ D.﹣5
5.如图,数轴上表示数﹣2的相反数的点是( )
A.点P B.点Q C.点M D.点N
BA(1). |-21|+|0|- |7|
(2)|-3| × |6.2|
我来试试计算:解:原式 = 21+0-7
= 14解:原式 = 3 × 6.2
= 18.6做一做 (1) 将- 1.5 , - 3 , - 1 ,- 5按从小到大的顺序排列。| -1.5 | = 1.5 ; | - 3 | = 3 | -1 | = 1 ; | - 5 | = 5.
(2) 求出- 1.5 , - 3 , - 1 , - 5的绝对值,并比较它们的大小。1 < 1.5 <3 <5-5 < -3 < -1.5 < -1 两个负数比较大小,绝对值大的反而小解法一(利用绝对值比较两个负数的大小)解: (1)| -1| = 1,| -5 | = 5 ,1﹤5,所以 - 1> - 5例题解法二 (利用数轴比较两个负数的大小)
(2)解:(1)因为- 5在 –1左边,所以 - 5﹤ - 1±422-67.220 老师,我来!比一比,看谁做得快又准!挑战自我01解:当|a|=0,|b-1|=0时, |a|+|b-1|=0
由|a|=0, 得a=0
|b-1|=0,即b-1=0, b=1已知|x-2|+|y- |=0,求2x+3y的值. 由|x-2|=0,得x=2
|y- |=0y=所以:2x+3y
=2 ×2 +3 ×
=5
挑战自我解:课时 小结:说一说,这节课你学到了什么?(1)绝对值的概念。(2)如何求一个数的绝对值。(3) 一个数的绝对值总是大于或等于0的。谢谢
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
