人教新课标A版必修3第二章 统计2.2.1用样本分布估计总体分布课件(共38张PPT)
文档属性
| 名称 | 人教新课标A版必修3第二章 统计2.2.1用样本分布估计总体分布课件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 15:21:45 | ||
图片预览








文档简介
(共38张PPT)
2.2 用样本估计总体
2.2.1 用样本的频率分布估计总体分布
2019.12
课程标准 学习要求 数学素养
1.通过对实例体会频率分布的意义和作用,在表示样本数据的过程中,学会列频率分布表,画频率分布直方图,频率分布折线图,茎叶图,体会它们各自的特点
2.在解决统计问题的过程中,体会用样本估计总体的思想,会用样本的频率分布估计总体分布 1.理解样本的频率分布估计总体分布的方法
2.会列频率分布表,画频率分布直方图,频率分布折线图,茎叶图
3.能够利用图形解决实际问题 数学抽象
直观想象
数据分析
数学运算
数学建模
1.用样本去估计总体是统计问题的一种基本思想
2.前面我们学过的抽样方法有:简单随机抽样、系统抽样、分层抽样
要注意这几种抽样方法的区别与联系
第一课时
3.初中时我们学习过频率分布,包括频数、频率的概念,频率分布表和频率分布直方图的制作。
复习回顾
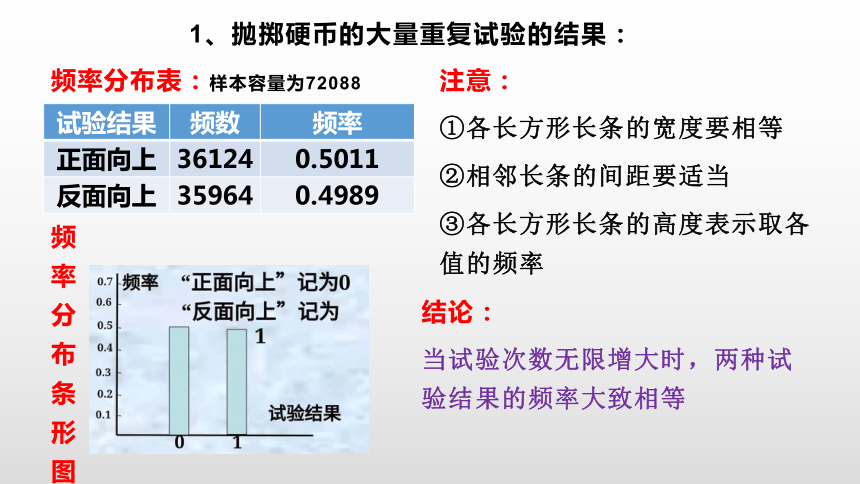
频率分布表:样本容量为72088
1、抛掷硬币的大量重复试验的结果:
频率分布条形图
试验结果 频数 频率
正面向上 36124 0.5011
反面向上 35964 0.4989
注意:
①各长方形长条的宽度要相等
②相邻长条的间距要适当
③各长方形长条的高度表示取各值的频率
结论:
当试验次数无限增大时,两种试验结果的频率大致相等
如何用样本的频率分布估计总体分布?
用样本分布
估计总体分布
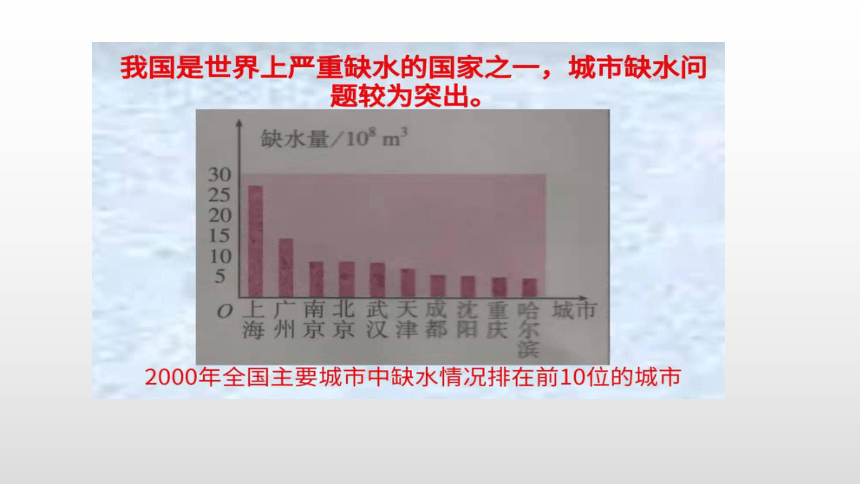
例1:某市政府为了节约生活用水,计划在本市试行居民用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超过a的部分按议价收费。
如果希望大部分居民的日常生活不受影响,那么标准a 定为多少比较合理呢?
为了较合理地确定这个标准,你认为需要做哪些工作?
如果标准太低,会影响居民日常生活;标准太高,则不利于节约用水。为了确定一个合理的标准,必修先了解居民的百分比情况等。
由于城市住户较多,需采用抽样调查的方式,通过分析样本数据来估计全市居民用水量的分布情况。
频率分布直方图制作步骤:
1.求极差:
4.3-0.2=4.1
2.决定组距与组数:
组数= = =8.2
3.将数据分组(组距0.5,组数9)
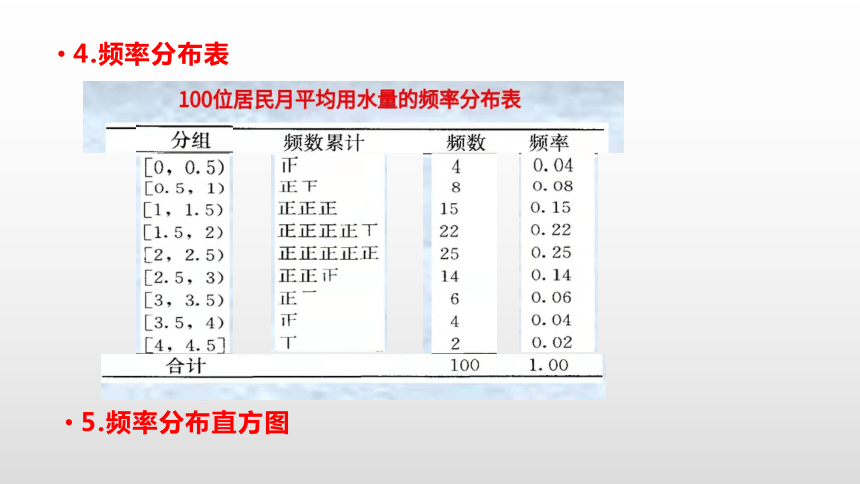
4.频率分布表
极差
组距
4.1
0.5
[0,0.5), [0.5,1), ... , [4.4.5]
4.频率分布表
5.频率分布直方图
5.频率分布直方图
小长方形的面积
=
组距×
频率
组距
=
频率
注意:
②某个区间上的频率这个区间的面积表示
①这里纵坐标不是频率,而是
频率
组距
思考:所有小长方形的面积之和= ?
1
宽度:组距
频率
组距
高度:
各小长方形的面积=频率
所有小长方形的面积之和=1
宽度:组距
频率
组距
高度:
(1)居民月均用水量的分布是“山峰”状的,而且是“单峰”的;
(2)大部分居民的月均用水量集中在一个中间值附近,只有少数居民的月均用水量很多或很少;
(3)居民月均用水量的分布有一定的对称性等。
画一组数据的频率分布直方图,可以按以下的步骤进行:
1.求极差,即数据中最大数与最小数的差
2.决定组距与组数:组距=极差/组数
3.分组:即通常对组内数据所在区间取左闭右开区间,最后一组取闭区间
4.统计频数、计算频率,列出频率分布表.
5.画出频率分布直方图(纵轴表示 :频率/组距)
解:组距为3
(1)频率分布表如下:
分组 频数 频率 频率/组距
[12.5 , 15.5) 3 0.06 0.020
[15.5 , 18.5) 8 0.16 0.053
[18.5 , 21.5) 9 0.18 0.060
[21.5 , 24.5) 11 0.22 0.073
[24.5 , 27.5) 10 0.20 0.067
[27.5 , 30.5) 5 0.10 0.033
[30.5 , 33.5) 4 0.08 0.027
合计 50 1.00
(2)
(3)数据在[15.5,24.5)的百分比是0.56
2.为检测某种产品的质量,抽取了一个容量为30的样本,检测结果为一级品5件,二级品8件,三级品13件,次品4件。
(1)列出样本频率分布表;
(2)画出表示样本频率分布的条形图;
(3)根据上述结果,估计此种产品为二级品或三级品的概率是多少?
解:(1)样本的频率分布表:
产品 频数 频率
一级品 5 0.17
二级品 8 0.27
三级品 13 0.43
次品 4 0.13
(2)样本的频率分布条形图:
(3)此种产品为二级品或三级品的概率是0.70
3.一个容量为100 的样本,数据的分组和各组的相关信息如下表,试完成下表。
分组 频数 频率 频率累计
[12 , 15) 6
[15 , 18) 0.08
[18 , 21) 0.30
[21 , 24) 21
[24 , 27) 0.69
[27 , 30) 16
[30 , 33) 0.10
[33 , 36) 1.00
合计 100 1.00
课堂小结:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.分组
4.列频率分布表
5.画频率分布直方图
第二课时
探究
知识回顾:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.分组
4.列频率分布表
5.画频率分布直方图
频率分布折线图
连接频率分布正方体中各个小正方形上端中点的折线,叫做频率分布折线图
当样本容量无限增大,分组的组距无限缩小,那么频率分布折线图就会无限接近一条光滑曲线
总体密度曲线
a
b
总体在区间[a , b]内取值的频率S
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具
用样本分布直方图去估计相应的总体时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即精确地反映了总体在各个i范围内取值的百分比
总体密度曲线
应用举例
例1:对于电子元件进行寿命追踪调查,情况如下:
(1)列出频率分布表 ;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100h~400h以内的频率;
(4)估计电子元件寿命在400h以上的频率;
寿命 100~200 200~300 300~400 400~500 500~600
个数 20 30 80 40 30
频率分布表
分组 频数 频率 频率累计
100~200 20 0,10 0.10
200~300 30 0.15 0.25
300~400 80 0,40 0.65
400~500 40 0.20 0.85
500~600 30 0.15 1.00
合计 200 1.00
频率分布直方图
(3)估计电子元件寿命在100h~400h以内的频率0.65
(4)估计电子元件寿命在400h以上的频率0.35
茎叶图
初中我们学过平均数、众数和中位数反映总体的水平,用方差考察稳定程度。
我们还有一种简易方法,就是将这些数据有条理的列出来,从中观察数据的分布情况,这种方法就是茎叶图。
制作茎叶图方法
将所有两位数的十位作为“茎“,个位作为”叶”,茎相同者
共用一个茎,茎按从大到小(或从小到大)的顺序同行列出
例1:某篮球运动员在赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,37,39,44,49,50
茎叶图
1
2
3
4
5
茎:
十位
数字
叶:
个位
数字
25
45
116679
49
0
注意:1.重复出现的数字要重复记录,不能遗漏;特别是“叶部分;
2.所有的信息都可以从这个茎叶图中得到
3.茎叶图便于记录和表示,
4.不足的是其分析只是粗略的,对差异不大的两组数据不易分析,
表示三位数以上的数据时不够方便
5.数据较多时,表示也不太方便
例2:甲、乙两运动员在某赛季每场比赛的得分的原始记录如下:
甲得分:13,51,23,8,26,38,16,33,14,28,39
乙得分:49,24,12,31,50,31,44,36,15,37,25,36,39.
甲
乙
0
1
2
3
4
5
0
25
54
161679
49
0
8
463
368
389
0
茎
叶
叶
小结:
图形 优点 缺点
频率分布直方图 易表示大量数据
直观表明分布情况 丢失一些信息
茎叶图 无信息损失
随时记录,方便记录和表示 只能处理样本容量较小数据
课堂小结:
4.茎叶图
样本频率分布直方图接近于一条光滑曲线 -----总体密度曲线,反映了总体分布
作业:
P71 练习 1. 2. 3
2.2 用样本估计总体
2.2.1 用样本的频率分布估计总体分布
2019.12
课程标准 学习要求 数学素养
1.通过对实例体会频率分布的意义和作用,在表示样本数据的过程中,学会列频率分布表,画频率分布直方图,频率分布折线图,茎叶图,体会它们各自的特点
2.在解决统计问题的过程中,体会用样本估计总体的思想,会用样本的频率分布估计总体分布 1.理解样本的频率分布估计总体分布的方法
2.会列频率分布表,画频率分布直方图,频率分布折线图,茎叶图
3.能够利用图形解决实际问题 数学抽象
直观想象
数据分析
数学运算
数学建模
1.用样本去估计总体是统计问题的一种基本思想
2.前面我们学过的抽样方法有:简单随机抽样、系统抽样、分层抽样
要注意这几种抽样方法的区别与联系
第一课时
3.初中时我们学习过频率分布,包括频数、频率的概念,频率分布表和频率分布直方图的制作。
复习回顾
频率分布表:样本容量为72088
1、抛掷硬币的大量重复试验的结果:
频率分布条形图
试验结果 频数 频率
正面向上 36124 0.5011
反面向上 35964 0.4989
注意:
①各长方形长条的宽度要相等
②相邻长条的间距要适当
③各长方形长条的高度表示取各值的频率
结论:
当试验次数无限增大时,两种试验结果的频率大致相等
如何用样本的频率分布估计总体分布?
用样本分布
估计总体分布
例1:某市政府为了节约生活用水,计划在本市试行居民用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超过a的部分按议价收费。
如果希望大部分居民的日常生活不受影响,那么标准a 定为多少比较合理呢?
为了较合理地确定这个标准,你认为需要做哪些工作?
如果标准太低,会影响居民日常生活;标准太高,则不利于节约用水。为了确定一个合理的标准,必修先了解居民的百分比情况等。
由于城市住户较多,需采用抽样调查的方式,通过分析样本数据来估计全市居民用水量的分布情况。
频率分布直方图制作步骤:
1.求极差:
4.3-0.2=4.1
2.决定组距与组数:
组数= = =8.2
3.将数据分组(组距0.5,组数9)
4.频率分布表
极差
组距
4.1
0.5
[0,0.5), [0.5,1), ... , [4.4.5]
4.频率分布表
5.频率分布直方图
5.频率分布直方图
小长方形的面积
=
组距×
频率
组距
=
频率
注意:
②某个区间上的频率这个区间的面积表示
①这里纵坐标不是频率,而是
频率
组距
思考:所有小长方形的面积之和= ?
1
宽度:组距
频率
组距
高度:
各小长方形的面积=频率
所有小长方形的面积之和=1
宽度:组距
频率
组距
高度:
(1)居民月均用水量的分布是“山峰”状的,而且是“单峰”的;
(2)大部分居民的月均用水量集中在一个中间值附近,只有少数居民的月均用水量很多或很少;
(3)居民月均用水量的分布有一定的对称性等。
画一组数据的频率分布直方图,可以按以下的步骤进行:
1.求极差,即数据中最大数与最小数的差
2.决定组距与组数:组距=极差/组数
3.分组:即通常对组内数据所在区间取左闭右开区间,最后一组取闭区间
4.统计频数、计算频率,列出频率分布表.
5.画出频率分布直方图(纵轴表示 :频率/组距)
解:组距为3
(1)频率分布表如下:
分组 频数 频率 频率/组距
[12.5 , 15.5) 3 0.06 0.020
[15.5 , 18.5) 8 0.16 0.053
[18.5 , 21.5) 9 0.18 0.060
[21.5 , 24.5) 11 0.22 0.073
[24.5 , 27.5) 10 0.20 0.067
[27.5 , 30.5) 5 0.10 0.033
[30.5 , 33.5) 4 0.08 0.027
合计 50 1.00
(2)
(3)数据在[15.5,24.5)的百分比是0.56
2.为检测某种产品的质量,抽取了一个容量为30的样本,检测结果为一级品5件,二级品8件,三级品13件,次品4件。
(1)列出样本频率分布表;
(2)画出表示样本频率分布的条形图;
(3)根据上述结果,估计此种产品为二级品或三级品的概率是多少?
解:(1)样本的频率分布表:
产品 频数 频率
一级品 5 0.17
二级品 8 0.27
三级品 13 0.43
次品 4 0.13
(2)样本的频率分布条形图:
(3)此种产品为二级品或三级品的概率是0.70
3.一个容量为100 的样本,数据的分组和各组的相关信息如下表,试完成下表。
分组 频数 频率 频率累计
[12 , 15) 6
[15 , 18) 0.08
[18 , 21) 0.30
[21 , 24) 21
[24 , 27) 0.69
[27 , 30) 16
[30 , 33) 0.10
[33 , 36) 1.00
合计 100 1.00
课堂小结:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.分组
4.列频率分布表
5.画频率分布直方图
第二课时
探究
知识回顾:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.分组
4.列频率分布表
5.画频率分布直方图
频率分布折线图
连接频率分布正方体中各个小正方形上端中点的折线,叫做频率分布折线图
当样本容量无限增大,分组的组距无限缩小,那么频率分布折线图就会无限接近一条光滑曲线
总体密度曲线
a
b
总体在区间[a , b]内取值的频率S
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具
用样本分布直方图去估计相应的总体时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即精确地反映了总体在各个i范围内取值的百分比
总体密度曲线
应用举例
例1:对于电子元件进行寿命追踪调查,情况如下:
(1)列出频率分布表 ;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100h~400h以内的频率;
(4)估计电子元件寿命在400h以上的频率;
寿命 100~200 200~300 300~400 400~500 500~600
个数 20 30 80 40 30
频率分布表
分组 频数 频率 频率累计
100~200 20 0,10 0.10
200~300 30 0.15 0.25
300~400 80 0,40 0.65
400~500 40 0.20 0.85
500~600 30 0.15 1.00
合计 200 1.00
频率分布直方图
(3)估计电子元件寿命在100h~400h以内的频率0.65
(4)估计电子元件寿命在400h以上的频率0.35
茎叶图
初中我们学过平均数、众数和中位数反映总体的水平,用方差考察稳定程度。
我们还有一种简易方法,就是将这些数据有条理的列出来,从中观察数据的分布情况,这种方法就是茎叶图。
制作茎叶图方法
将所有两位数的十位作为“茎“,个位作为”叶”,茎相同者
共用一个茎,茎按从大到小(或从小到大)的顺序同行列出
例1:某篮球运动员在赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,37,39,44,49,50
茎叶图
1
2
3
4
5
茎:
十位
数字
叶:
个位
数字
25
45
116679
49
0
注意:1.重复出现的数字要重复记录,不能遗漏;特别是“叶部分;
2.所有的信息都可以从这个茎叶图中得到
3.茎叶图便于记录和表示,
4.不足的是其分析只是粗略的,对差异不大的两组数据不易分析,
表示三位数以上的数据时不够方便
5.数据较多时,表示也不太方便
例2:甲、乙两运动员在某赛季每场比赛的得分的原始记录如下:
甲得分:13,51,23,8,26,38,16,33,14,28,39
乙得分:49,24,12,31,50,31,44,36,15,37,25,36,39.
甲
乙
0
1
2
3
4
5
0
25
54
161679
49
0
8
463
368
389
0
茎
叶
叶
小结:
图形 优点 缺点
频率分布直方图 易表示大量数据
直观表明分布情况 丢失一些信息
茎叶图 无信息损失
随时记录,方便记录和表示 只能处理样本容量较小数据
课堂小结:
4.茎叶图
样本频率分布直方图接近于一条光滑曲线 -----总体密度曲线,反映了总体分布
作业:
P71 练习 1. 2. 3
