人教版七年级上册3.4实际问题与一元一次方程课件 (共28张PPT)
文档属性
| 名称 | 人教版七年级上册3.4实际问题与一元一次方程课件 (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 11:28:20 | ||
图片预览







文档简介
(共28张PPT)
3.4 实际问题与一元一次方程
第三课时
回顾列一元一次方程解应用题的一般步骤.
审、设、列、解、验、答.
活动1
探究一:商品销售问题中的基本量
生活中的我们都会经常去买东西,看似很熟悉的问题,但大部分同学根本就不知道买东西的过程中要涉及到所买商品的售价、进价、利润、利润率等因素,那到底什么是进价、售价、利润呢?
举例:夏天的时候,天气炎热,有个同学去买了一支1元钱的冰棍,假设老板批发冰棍的时候是5毛钱一支,那这个老板赚多少钱呢?(不考虑冰棍损耗和其他费用)
通过举生活中的例子,回顾旧知
活动1
探究一:商品销售问题中的基本量
通过举生活中的例子,回顾旧知
总结:
去买冰棍的1元钱就是冰棍的售价;而批发的时候只需要5毛钱一支,这个5毛就是成本,也就是进价;买一支冰棍老板赚了5毛,而这个5毛就是利润.
活动2
探究一:商品销售问题中的基本量
热身练习
填空:(1)某商品原来每件零售价是a元,现在每件降价10%,降价后每件零售价是_______;
(2)安踏运动鞋打八折后是220元,则原价是____元;
(3)进价为80元的篮球,卖了120元,利润是____元,利润率是______;
(4)某商场将进价为1980元的电视按标价的八折出售仍获利10%,则该商品的标价为______元;
你能快速、准确地填空吗?
活动2
探究一:商品销售问题中的基本量
热身练习
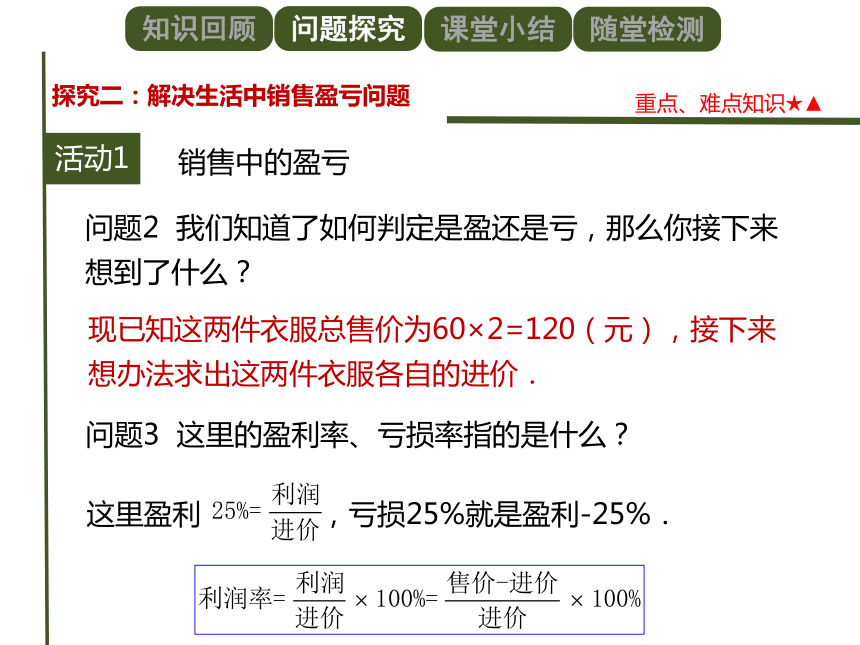
总结:在商品销售问题中的常常与商品的“进价”“标价”“售价” “利润”及“利润率”等词语相关,这些量间的关系是:利润=售价-进价;
售价=标价× =进价×(1+利润率).
活动1
探究二:解决生活中销售盈亏问题
某商店的某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
重点、难点知识★▲
问题1 如何判定是盈利还是亏损?
销售中的盈亏
卖这两件衣服总的是盈利还是亏损,取决于这两件衣服售价多少,进价多少,若售价大于进价,就盈利,若售价小于进价,就亏损.
活动1
探究二:解决生活中销售盈亏问题
现已知这两件衣服总售价为60×2=120(元),接下来想办法求出这两件衣服各自的进价.
重点、难点知识★▲
这里盈利 ,亏损25%就是盈利-25%.
问题2 我们知道了如何判定是盈还是亏,那么你接下来想到了什么?
销售中的盈亏
问题3 这里的盈利率、亏损率指的是什么?
活动2
探究二:解决生活中销售盈亏问题
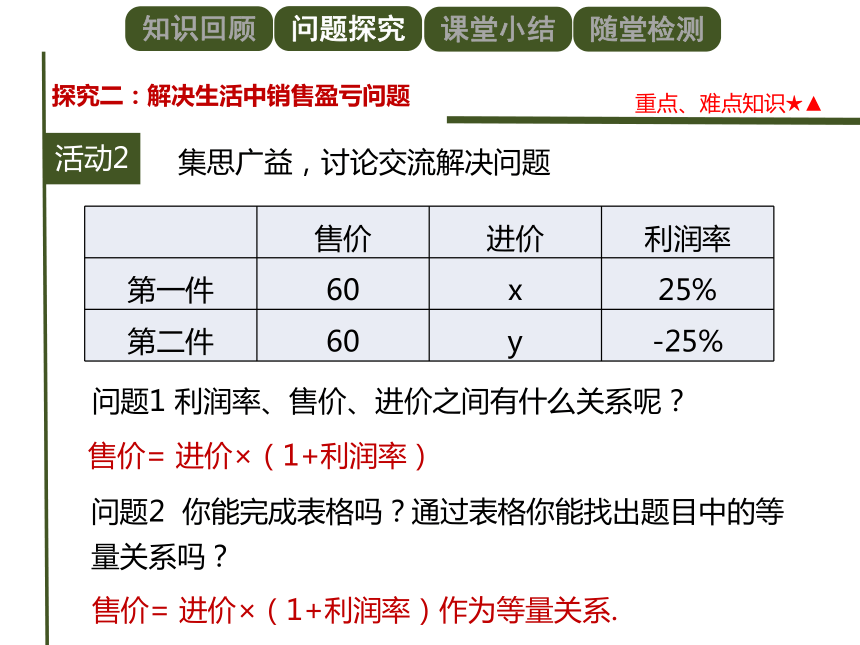
售价= 进价×(1+利润率)
重点、难点知识★▲
问题1 利润率、售价、进价之间有什么关系呢?
集思广益,讨论交流解决问题
问题2 你能完成表格吗?通过表格你能找出题目中的等量关系吗?
售价= 进价×(1+利润率)作为等量关系.
? 售价 进价 利润率
第一件 60 x 25%
第二件 60 y -25%
活动2
探究二:解决生活中销售盈亏问题
(1+25%)x=60;(1-25%)y=60
重点、难点知识★▲
问题3 你能根据相等关系列出方程吗?
集思广益,讨论交流解决问题
问题4 你能完整解答本题吗?
活动2
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
集思广益,讨论交流解决问题
解:设盈利25%的那件衣服的进价是x元,另一件亏损25%的那件衣服进价是y元.
由题意得:(1+25%)x=60;(1-25%)y=60,
解得:x=48,y=80 .
∴两件衣服共进价128元,而两件衣服的售价和为120元,进价大于售价,由此可知卖这两件衣服总的盈亏情况是亏损8元.
活动2
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
集思广益,讨论交流解决问题
解决销售中的利润问题,一定掌握进价、售价、标价、利润、利润率、打折等概念和它们之间的基本数量关系:
利润=售价-进价;
售价=标价 × =进价×(1+利润率)
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
解方程后得出的结论与你先前的估算一致吗?你是怎样估算的?
其中一件衣服是盈利25%后,才卖60元,那么这件衣服进价一定比60元低.另一件衣服亏损25%后,还卖60元,说明这件衣服进价一定比60元高,由此可知亏损25%的这件进价高,所以卖这两件衣服总的还是亏损.
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
点评:不要认为一件盈利25%,一件亏损25%,结果不盈不亏,因为盈亏要看这两件的进价.例如盈利25%的一件进价为40元,那么这一件盈利40%×25%=10(元),亏损25%的一件进价为80元,那么这一件亏损了80×25%=20(元),总的还是亏损10元,这就是说,亏损25%的一件进价如果比盈利25%的一件进价高,那么总的是亏损,反之才是盈利.
总结:有关销售盈亏问题的应用题中:
(1)当利润值为正数时是盈利,当利润值为负数时为亏损;
(2) ;
(3)“先估算,后准确计算”是分析问题的通常顺序.
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
活动1
探究三:运用知识解决问题
通过前面的探究,我们知道了利用一元一次方程解决实际问题的基本过程,利用这些步骤和方法可以解决一些怎样的销售问题呢?
例1 某校七年级社会实践小组去商店调查商品销售情况,了解到该商店以每条80元的价格购进了某品牌牛仔裤50条,并以每条120元的价格销售了40条.商店准备采取促销措施,将剩下的牛仔裤降价销售.请你帮商店计算一下,每条牛仔裤降价多少元时,销售完这批牛仔裤正好达到盈利45%的预期目标?
重点、难点知识★▲
活动1
探究三:运用知识解决问题
【解题过程】
解:设每条牛仔裤降价x元,
根据题意得: ,
解得:x=20.
答:每条牛仔裤降价20元时,销售完这批牛仔裤正好达到盈利45%的预期目标.
【思路点拨】根据销售总价=成本×(1+45%)列出关于x的一元一次方程即可.
重点、难点知识★▲
活动1
探究三:运用知识解决问题
练习:某种商品因换季准备打折出售,如果按定价的七五折出售,将赔25元,而按定价的九折出售,将赚20元,这种商品的定价是多少元?
【解题过程】
解:设这种商品的定价是x元,
根据题意得: ,解得:x=300
答:这种商品的定价是300元.
重点、难点知识★▲
【思路点拨】本题的进价是个定值,抓七五折出售的进价=九折出售的进价,弄清打折的概念和有关利润的计算公式.
活动2
探究三:运用知识解决问题
练习:小明在商店里看中了一件夹克衫,店家说:“我这儿所有商品都是在进价上加50%的利润再标价的,这件夹克衫我给你按标价打8折,你就付168元,我可只赚了你8元钱啊!”聪明的小明经过思考后觉得店家的说法不可信,请你通过计算说明店家是否诚信?
重点、难点知识★▲
【思路点拨】设进价是x元,根据售价是168元,可列方程,解方程即可求得进价,再算出利润与8元比较即可.
【解题过程】解:设进价是x元,根据题意得:1.5×0.8x=168,解得:x=140.
则168﹣140=28,∴赚了28块,所以店家在撒谎.
活动3
探究三:运用知识解决问题
例3:
重点、难点知识★▲
(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
解:(1)当一次性购物标价总额是300元时,甲超市实付款=300×0.88=264(元),乙超市实付款=300×0.9=270(元);
(2)设当标价总额是x元时,甲、乙超市实付款一样.当一次性购物标价总额是500元时,甲超市实付款=500×0.88=440(元),乙超市实付款=500×0.9=450(元),
∵440<450,∴x>500 .根据题意得0.88x=500×0.9+0.8(x-500),解得 x=625.
答:当标价总额是625元时,甲、乙超市实付款一样;
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
(3)小王两次到乙超市分别购物付款198元和466元,
第一次购物付款198元,购物标价可能是198元,也可能是198÷0.9=220元,
第二次购物付款466元,购物标价是(466﹣450)÷0.8+500=520元,
两次购物标价之和是198+520=718元,或220+520=740元.
若他只去一次该超市购买同样多的商品,
实付款500×0.9+0.8(718﹣500)=624.4元,或500×0.9+0.8(740﹣500)=642元,
可以节省198+466﹣624.4=39.6元,或198+466﹣642=22元.
答:若他只去一次该超市购买同样多的商品,可以节省39.6或22元.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【思路点拨】
(1)根据两家超市的优惠方案,可知当一次性购物标价总额是300元时,甲超市实付款=购物标价×0.88,乙超市实付款=300×0.9,分别计算即可;
(2)设当标价总额是x元时,甲、乙超市实付款一样.根据甲超市实付款=乙超市实付款列出方程,求解即可;
(3)首先计算出两次购物标价,然后根据优惠方案即可求解.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
练习:某书城开展学生优惠购书活动,凡一次性购买不超过200元的一律九折优惠;超过200元的,其中200元按九折计算,超过200元的部分按八折计算.某学生第一次去购书付款72元,第二次去购书享受了八折优惠,他查看了所买书的定价,发现两次共节约了34元,则该学生第二次购书实际付款多少元?
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
解:第一次购书付款72元,享受了九折优惠,实际定价为72÷0.9=80元,省去了80-72=8元钱.依题意,第二次节省了34-8=26元.第二次的定价超过了200元.
设第二次所购书的定价为x元.
(x-200)×0.8+200×0.9=x-26,解得x=230 .
故第二次购书实际付款为230-26=204元.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【思路点拨】
先求出第一次买书所优惠的钱数,再求出第二次购书优惠的钱数是分两部分优惠(200元按九折计算,超过200元的部分按八折优惠),进一步分两种情况设出原价,表示出第二次优惠的钱数,列方程解答即可.
解答本题需注意第二次所购的书有九折的部分,有八折的部分,需清楚找到这两部分实际出的钱.
知识梳理
(1)列一元一次方程解决实际问题的一般步骤:
审、设、列、解、检、答.
(2)解决商品销售的盈亏问题类型的应用题,首先要弄清商品利润、商品进价、售价、标价,打折的意义,以及它们之间的关系:
利润=售价-进价 ;
售价= 标价 × =进价×(1+利润率).
(3)然后分析题目中的数量关系,找出能表示题目全部意义的相等关系,根据这个相等关系列出方程,求出方程的解后,一定要检验解的合理性.
重难点突破
(1)商品的“进价”“标价”“售价” “利润”及“利润率”这些量间的关系.
(2)找出相等关系,列出方程后,一定要检验解的合理性.
(3)打折问题中涉及的分类讨论思想的运用.
3.4 实际问题与一元一次方程
第三课时
回顾列一元一次方程解应用题的一般步骤.
审、设、列、解、验、答.
活动1
探究一:商品销售问题中的基本量
生活中的我们都会经常去买东西,看似很熟悉的问题,但大部分同学根本就不知道买东西的过程中要涉及到所买商品的售价、进价、利润、利润率等因素,那到底什么是进价、售价、利润呢?
举例:夏天的时候,天气炎热,有个同学去买了一支1元钱的冰棍,假设老板批发冰棍的时候是5毛钱一支,那这个老板赚多少钱呢?(不考虑冰棍损耗和其他费用)
通过举生活中的例子,回顾旧知
活动1
探究一:商品销售问题中的基本量
通过举生活中的例子,回顾旧知
总结:
去买冰棍的1元钱就是冰棍的售价;而批发的时候只需要5毛钱一支,这个5毛就是成本,也就是进价;买一支冰棍老板赚了5毛,而这个5毛就是利润.
活动2
探究一:商品销售问题中的基本量
热身练习
填空:(1)某商品原来每件零售价是a元,现在每件降价10%,降价后每件零售价是_______;
(2)安踏运动鞋打八折后是220元,则原价是____元;
(3)进价为80元的篮球,卖了120元,利润是____元,利润率是______;
(4)某商场将进价为1980元的电视按标价的八折出售仍获利10%,则该商品的标价为______元;
你能快速、准确地填空吗?
活动2
探究一:商品销售问题中的基本量
热身练习
总结:在商品销售问题中的常常与商品的“进价”“标价”“售价” “利润”及“利润率”等词语相关,这些量间的关系是:利润=售价-进价;
售价=标价× =进价×(1+利润率).
活动1
探究二:解决生活中销售盈亏问题
某商店的某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
重点、难点知识★▲
问题1 如何判定是盈利还是亏损?
销售中的盈亏
卖这两件衣服总的是盈利还是亏损,取决于这两件衣服售价多少,进价多少,若售价大于进价,就盈利,若售价小于进价,就亏损.
活动1
探究二:解决生活中销售盈亏问题
现已知这两件衣服总售价为60×2=120(元),接下来想办法求出这两件衣服各自的进价.
重点、难点知识★▲
这里盈利 ,亏损25%就是盈利-25%.
问题2 我们知道了如何判定是盈还是亏,那么你接下来想到了什么?
销售中的盈亏
问题3 这里的盈利率、亏损率指的是什么?
活动2
探究二:解决生活中销售盈亏问题
售价= 进价×(1+利润率)
重点、难点知识★▲
问题1 利润率、售价、进价之间有什么关系呢?
集思广益,讨论交流解决问题
问题2 你能完成表格吗?通过表格你能找出题目中的等量关系吗?
售价= 进价×(1+利润率)作为等量关系.
? 售价 进价 利润率
第一件 60 x 25%
第二件 60 y -25%
活动2
探究二:解决生活中销售盈亏问题
(1+25%)x=60;(1-25%)y=60
重点、难点知识★▲
问题3 你能根据相等关系列出方程吗?
集思广益,讨论交流解决问题
问题4 你能完整解答本题吗?
活动2
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
集思广益,讨论交流解决问题
解:设盈利25%的那件衣服的进价是x元,另一件亏损25%的那件衣服进价是y元.
由题意得:(1+25%)x=60;(1-25%)y=60,
解得:x=48,y=80 .
∴两件衣服共进价128元,而两件衣服的售价和为120元,进价大于售价,由此可知卖这两件衣服总的盈亏情况是亏损8元.
活动2
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
集思广益,讨论交流解决问题
解决销售中的利润问题,一定掌握进价、售价、标价、利润、利润率、打折等概念和它们之间的基本数量关系:
利润=售价-进价;
售价=标价 × =进价×(1+利润率)
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
解方程后得出的结论与你先前的估算一致吗?你是怎样估算的?
其中一件衣服是盈利25%后,才卖60元,那么这件衣服进价一定比60元低.另一件衣服亏损25%后,还卖60元,说明这件衣服进价一定比60元高,由此可知亏损25%的这件进价高,所以卖这两件衣服总的还是亏损.
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
点评:不要认为一件盈利25%,一件亏损25%,结果不盈不亏,因为盈亏要看这两件的进价.例如盈利25%的一件进价为40元,那么这一件盈利40%×25%=10(元),亏损25%的一件进价为80元,那么这一件亏损了80×25%=20(元),总的还是亏损10元,这就是说,亏损25%的一件进价如果比盈利25%的一件进价高,那么总的是亏损,反之才是盈利.
总结:有关销售盈亏问题的应用题中:
(1)当利润值为正数时是盈利,当利润值为负数时为亏损;
(2) ;
(3)“先估算,后准确计算”是分析问题的通常顺序.
活动3
探究二:解决生活中销售盈亏问题
重点、难点知识★▲
反思过程,发现规律
活动1
探究三:运用知识解决问题
通过前面的探究,我们知道了利用一元一次方程解决实际问题的基本过程,利用这些步骤和方法可以解决一些怎样的销售问题呢?
例1 某校七年级社会实践小组去商店调查商品销售情况,了解到该商店以每条80元的价格购进了某品牌牛仔裤50条,并以每条120元的价格销售了40条.商店准备采取促销措施,将剩下的牛仔裤降价销售.请你帮商店计算一下,每条牛仔裤降价多少元时,销售完这批牛仔裤正好达到盈利45%的预期目标?
重点、难点知识★▲
活动1
探究三:运用知识解决问题
【解题过程】
解:设每条牛仔裤降价x元,
根据题意得: ,
解得:x=20.
答:每条牛仔裤降价20元时,销售完这批牛仔裤正好达到盈利45%的预期目标.
【思路点拨】根据销售总价=成本×(1+45%)列出关于x的一元一次方程即可.
重点、难点知识★▲
活动1
探究三:运用知识解决问题
练习:某种商品因换季准备打折出售,如果按定价的七五折出售,将赔25元,而按定价的九折出售,将赚20元,这种商品的定价是多少元?
【解题过程】
解:设这种商品的定价是x元,
根据题意得: ,解得:x=300
答:这种商品的定价是300元.
重点、难点知识★▲
【思路点拨】本题的进价是个定值,抓七五折出售的进价=九折出售的进价,弄清打折的概念和有关利润的计算公式.
活动2
探究三:运用知识解决问题
练习:小明在商店里看中了一件夹克衫,店家说:“我这儿所有商品都是在进价上加50%的利润再标价的,这件夹克衫我给你按标价打8折,你就付168元,我可只赚了你8元钱啊!”聪明的小明经过思考后觉得店家的说法不可信,请你通过计算说明店家是否诚信?
重点、难点知识★▲
【思路点拨】设进价是x元,根据售价是168元,可列方程,解方程即可求得进价,再算出利润与8元比较即可.
【解题过程】解:设进价是x元,根据题意得:1.5×0.8x=168,解得:x=140.
则168﹣140=28,∴赚了28块,所以店家在撒谎.
活动3
探究三:运用知识解决问题
例3:
重点、难点知识★▲
(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
解:(1)当一次性购物标价总额是300元时,甲超市实付款=300×0.88=264(元),乙超市实付款=300×0.9=270(元);
(2)设当标价总额是x元时,甲、乙超市实付款一样.当一次性购物标价总额是500元时,甲超市实付款=500×0.88=440(元),乙超市实付款=500×0.9=450(元),
∵440<450,∴x>500 .根据题意得0.88x=500×0.9+0.8(x-500),解得 x=625.
答:当标价总额是625元时,甲、乙超市实付款一样;
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
(3)小王两次到乙超市分别购物付款198元和466元,
第一次购物付款198元,购物标价可能是198元,也可能是198÷0.9=220元,
第二次购物付款466元,购物标价是(466﹣450)÷0.8+500=520元,
两次购物标价之和是198+520=718元,或220+520=740元.
若他只去一次该超市购买同样多的商品,
实付款500×0.9+0.8(718﹣500)=624.4元,或500×0.9+0.8(740﹣500)=642元,
可以节省198+466﹣624.4=39.6元,或198+466﹣642=22元.
答:若他只去一次该超市购买同样多的商品,可以节省39.6或22元.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【思路点拨】
(1)根据两家超市的优惠方案,可知当一次性购物标价总额是300元时,甲超市实付款=购物标价×0.88,乙超市实付款=300×0.9,分别计算即可;
(2)设当标价总额是x元时,甲、乙超市实付款一样.根据甲超市实付款=乙超市实付款列出方程,求解即可;
(3)首先计算出两次购物标价,然后根据优惠方案即可求解.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
练习:某书城开展学生优惠购书活动,凡一次性购买不超过200元的一律九折优惠;超过200元的,其中200元按九折计算,超过200元的部分按八折计算.某学生第一次去购书付款72元,第二次去购书享受了八折优惠,他查看了所买书的定价,发现两次共节约了34元,则该学生第二次购书实际付款多少元?
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【解题过程】
解:第一次购书付款72元,享受了九折优惠,实际定价为72÷0.9=80元,省去了80-72=8元钱.依题意,第二次节省了34-8=26元.第二次的定价超过了200元.
设第二次所购书的定价为x元.
(x-200)×0.8+200×0.9=x-26,解得x=230 .
故第二次购书实际付款为230-26=204元.
活动3
探究三:运用知识解决问题
重点、难点知识★▲
【思路点拨】
先求出第一次买书所优惠的钱数,再求出第二次购书优惠的钱数是分两部分优惠(200元按九折计算,超过200元的部分按八折优惠),进一步分两种情况设出原价,表示出第二次优惠的钱数,列方程解答即可.
解答本题需注意第二次所购的书有九折的部分,有八折的部分,需清楚找到这两部分实际出的钱.
知识梳理
(1)列一元一次方程解决实际问题的一般步骤:
审、设、列、解、检、答.
(2)解决商品销售的盈亏问题类型的应用题,首先要弄清商品利润、商品进价、售价、标价,打折的意义,以及它们之间的关系:
利润=售价-进价 ;
售价= 标价 × =进价×(1+利润率).
(3)然后分析题目中的数量关系,找出能表示题目全部意义的相等关系,根据这个相等关系列出方程,求出方程的解后,一定要检验解的合理性.
重难点突破
(1)商品的“进价”“标价”“售价” “利润”及“利润率”这些量间的关系.
(2)找出相等关系,列出方程后,一定要检验解的合理性.
(3)打折问题中涉及的分类讨论思想的运用.
