人教A版高中数学必修3课件:2.2.2.2标准差(共16张PPT)
文档属性
| 名称 | 人教A版高中数学必修3课件:2.2.2.2标准差(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 07:06:34 | ||
图片预览






文档简介
(共16张PPT)
第二课时 标准差
1、知道标准差的意义;
2、能求样本的标准差。
认真阅读教材P74—78页内容,
提出你不懂的问题。
思考1:在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?
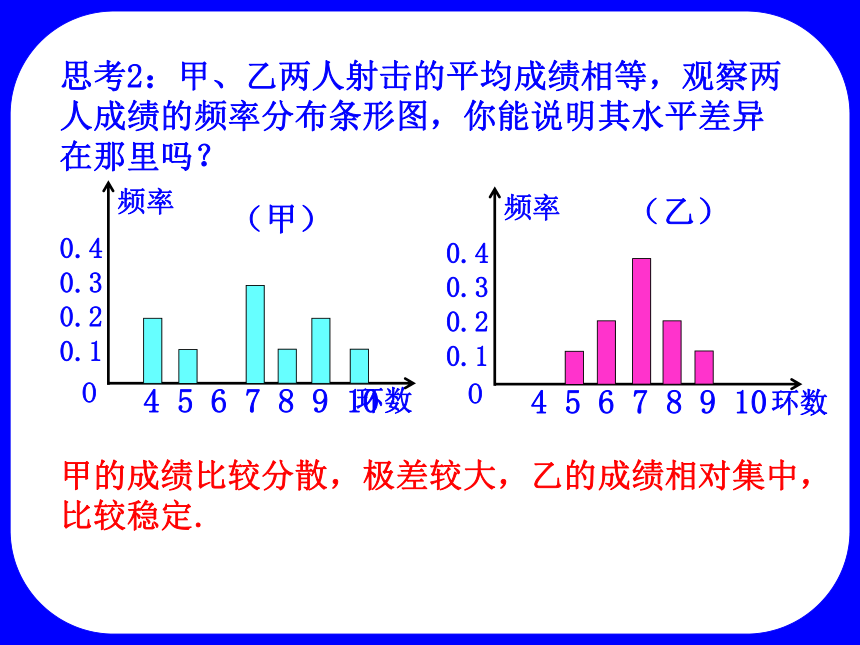
思考2:甲、乙两人射击的平均成绩相等,观察两人成绩的频率分布条形图,你能说明其水平差异在那里吗?
环数
甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.
思考3:对于样本数据x1,x2,…,xn,设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算?
思考4:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.假设样本数据x1,x2,…,xn的平均数为,则标准差的计算公式是:
那么标准差的取值范围是什么?标准差为0的样本数据有何特点?
s≥0,标准差为0的样本数据都相等.
思考5:对于一个容量为2的样本:x1,x2
(x1
在数轴上,这两个统计数据有什么几何意义?由此说明标准差的大小对数据的离散程度有何影响?
标准差越大离散程度越大,数据较分散;标准差越小离散程度越小,数据较集中在平均数周围.
补充
1.标准差的平方s?称为方差,有时用方差代替标准差测量样本数据的离散度.方差与标准差的测量效果是一致的,在实际应用中一般多采用标准差.
2.现实中的总体所包含的个体数往往很多,总体的平均数与标准差是未知的,我们通常用样本的平均数和标准差去估计总体的平均数与标准差,但要求样本有较好的代表性.
例题分析
例1 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
例2 甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):
甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39
乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48
从生产零件内径的尺寸看,谁生产的零件质量较高?
甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高.
说明:1.生产质量可以从总体的平均数与标准差两个角度来衡量,但甲、乙两个总体的平均数与标准差都是不知道的,我们就用样本的平均数与标准差估计总体的平均数与标准差.
2.问题中25.40mm是内径的标准值,而不是总体的平均数.
解: 依题意计算可得
x1=900 x2=900 s1≈23.8 s2 ≈42.6
甲乙两种水稻6年平均产量的平均数相同,但甲的标准差比乙的小,所以甲的生产比较稳定.
解 : (1) 平均重量约为496.86 g , 标准差约为6.55
第二课时 标准差
1、知道标准差的意义;
2、能求样本的标准差。
认真阅读教材P74—78页内容,
提出你不懂的问题。
思考1:在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?
思考2:甲、乙两人射击的平均成绩相等,观察两人成绩的频率分布条形图,你能说明其水平差异在那里吗?
环数
甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.
思考3:对于样本数据x1,x2,…,xn,设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算?
思考4:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.假设样本数据x1,x2,…,xn的平均数为,则标准差的计算公式是:
那么标准差的取值范围是什么?标准差为0的样本数据有何特点?
s≥0,标准差为0的样本数据都相等.
思考5:对于一个容量为2的样本:x1,x2
(x1
在数轴上,这两个统计数据有什么几何意义?由此说明标准差的大小对数据的离散程度有何影响?
标准差越大离散程度越大,数据较分散;标准差越小离散程度越小,数据较集中在平均数周围.
补充
1.标准差的平方s?称为方差,有时用方差代替标准差测量样本数据的离散度.方差与标准差的测量效果是一致的,在实际应用中一般多采用标准差.
2.现实中的总体所包含的个体数往往很多,总体的平均数与标准差是未知的,我们通常用样本的平均数和标准差去估计总体的平均数与标准差,但要求样本有较好的代表性.
例题分析
例1 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
例2 甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):
甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39
乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48
从生产零件内径的尺寸看,谁生产的零件质量较高?
甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高.
说明:1.生产质量可以从总体的平均数与标准差两个角度来衡量,但甲、乙两个总体的平均数与标准差都是不知道的,我们就用样本的平均数与标准差估计总体的平均数与标准差.
2.问题中25.40mm是内径的标准值,而不是总体的平均数.
解: 依题意计算可得
x1=900 x2=900 s1≈23.8 s2 ≈42.6
甲乙两种水稻6年平均产量的平均数相同,但甲的标准差比乙的小,所以甲的生产比较稳定.
解 : (1) 平均重量约为496.86 g , 标准差约为6.55
