人教版九年级数学上册教学讲义,复习补习资料(巩固练习):16.二次函数y=a(x-h)^2+k(a≠0)的图象与性质【基础】含答案
文档属性
| 名称 | 人教版九年级数学上册教学讲义,复习补习资料(巩固练习):16.二次函数y=a(x-h)^2+k(a≠0)的图象与性质【基础】含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 202.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 00:00:00 | ||
图片预览



文档简介
二次函数y=a(x-h)2+k(a≠0)的图象与性质—知识讲解(基础)
【学习目标】
1.会用描点法画出二次函数/(a、h、k常数,a≠0)的图象.掌握抛物线/与/图象之间的关系;
2.熟练掌握函数/的有关性质,并能用函数/的性质解决一些实际问题;
3.经历探索/的图象及性质的过程,体验/与/、/、/之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
/的符号
开口方向
顶点坐标
对称轴
性质
/
向上
/
x=h
/时,/随/的增大而增大;/时,/随/的增大而减小;/时,/有最小值/.
/
向下
/
x=h
/时,/随/的增大而减小;/时,/随/的增大而增大;/时,/有最大值/.
2.函数的图象与性质
/的符号
开口方向
顶点坐标
对称轴
性质
/
向上
/
x=h
/时,/随/的增大而增大;/时,/随/的增大而减小;/时,/有最小值/.
/
向下
/
x=h
/时,/随/的增大而减小;/时,/随/的增大而增大;/时,/有最大值/.
要点诠释:
二次函数/的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
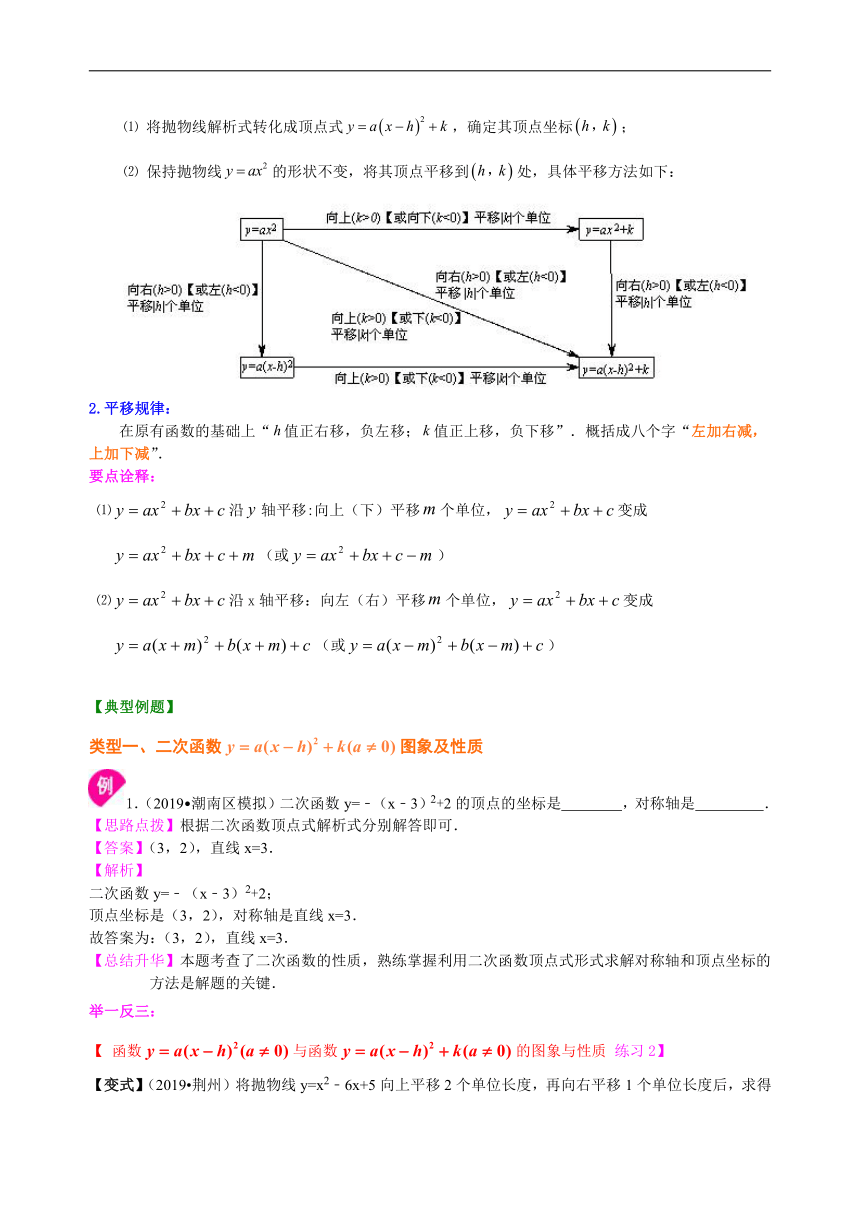
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式/,确定其顶点坐标/;
⑵ 保持抛物线/的形状不变,将其顶点平移到/处,具体平移方法如下:
/
2.平移规律:
在原有函数的基础上“/值正右移,负左移;/值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴/沿/轴平移:向上(下)平移/个单位,/变成
/(或/)
⑵/沿x轴平移:向左(右)平移/个单位,/变成/(或/)
【典型例题】
类型一、二次函数图象及性质
/1.(2019?潮南区模拟)二次函数y=﹣(x﹣3)2+2的顶点的坐标是 ,对称轴是 .
【思路点拨】根据二次函数顶点式解析式分别解答即可.
【答案】(3,2),直线x=3.
【解析】
二次函数y=﹣(x﹣3)2+2;
顶点坐标是(3,2),对称轴是直线x=3.
故答案为:(3,2),直线x=3.
【总结升华】本题考查了二次函数的性质,熟练掌握利用二次函数顶点式形式求解对称轴和顶点坐标的方法是解题的关键.
举一反三:
【 函数与函数的图象与性质 练习2】
【变式】(2019?荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
【答案与解析】
解:y=x2﹣6x+5=(x﹣3)2﹣4,
∴抛物线的顶点坐标为(3,﹣4),
把点(3,﹣4)向上平移2个单位长度,再向右平移1个单位长度得到点的坐标为(4,﹣2),
∴平移后得到的抛物线解析式为y=(x﹣4)2﹣2.
/2.把抛物线/向上平移2个单位,再向左平移4个单位,得到抛物线/,
求b,c的值. 【答案与解析】
根据题意得,y=(x-4)2-2=x2-8x+14, 所以 / 【总结升华】把抛物线/向上平移2个单位,再向左平移4个单位,得到抛物线/,
也就意味着把抛物线/向下平移2个单位,再向右平移4个单位,得到抛物线/.
举一反三:
【变式】二次函数/的图象可以看作是二次函数/的图象向 平移4个单位,再向 平移3个单位得到的.
【答案】上;右.
类型二、二次函数性质的综合应用
/3.(2019秋?安顺期末)二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
/
【答案与解析】
解:(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a=﹣/,
∴二次函数解析式为y1=﹣/(x﹣2)2=﹣/a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:/,
解得:k=/,b=﹣1,
则直线AB解析式为y=/x﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
【总结升华】可先由待定系数法建立方程组求出两个函数的解析式,然后利用函数图象写出自变量的取值范围.
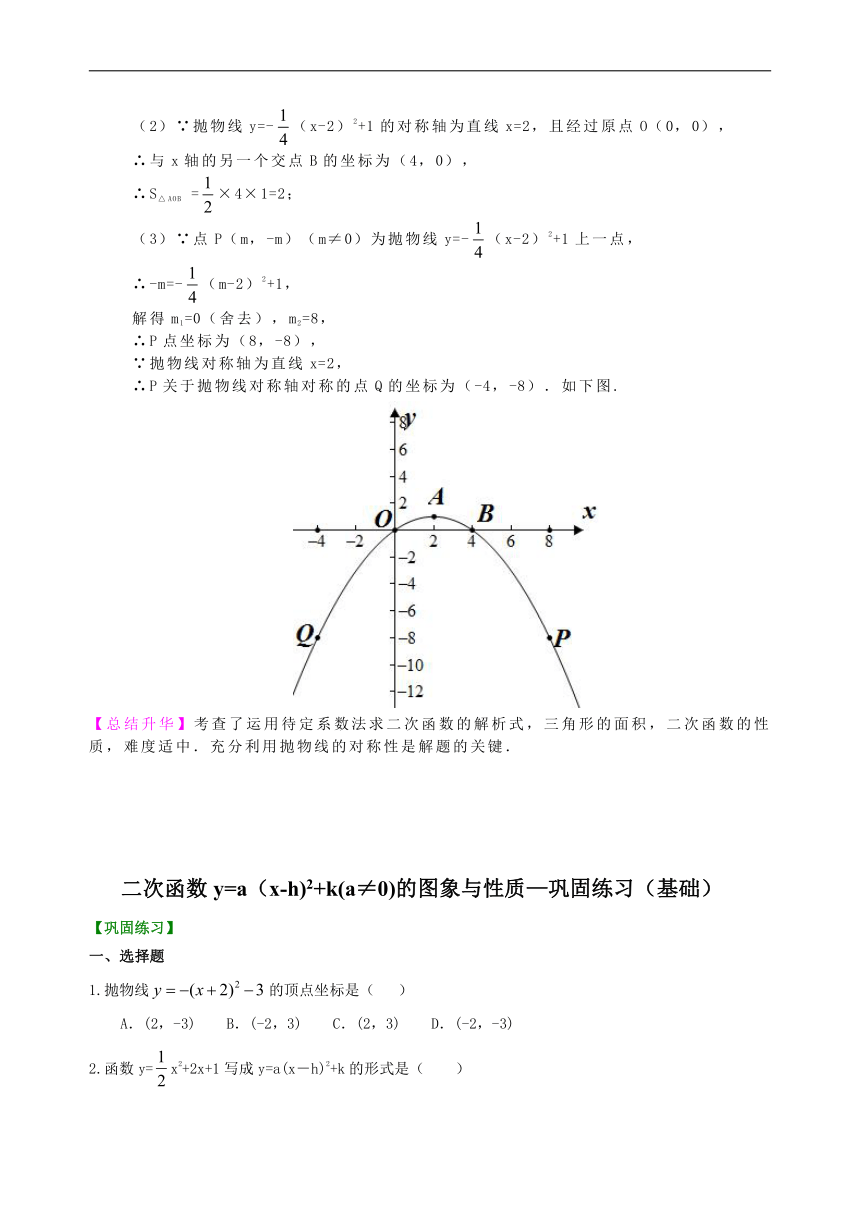
/4.如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B. (1)求抛物线的解析式; (2)求△AOB的面积; (3)若点P(m,-m)(m≠0)为抛物线上一点,求与P关于抛物线对称轴对称的点Q的
坐标.(注:抛物线y=ax2+bx+c的对称轴是x=-).
/
【思路点拨】(1)已知抛物线的顶点为A(2,1),设抛物线为顶点式y=a(x-h)2+k,把点O(0,0)代入即可求解析式; (2)由抛物线的对称轴为直线x=2,且经过原点O(0,0),根据对称性得出与x轴的另一个交点B的坐标,再根据三角形的面积公式即可求出△AOB的面积; (3)将点P(m,-m)代入y=-(x-2)2+1,得出-m=-(m-2)2+1,解方程求出m的值,得到P点坐标,再根据对称性即可求出P关于抛物线对称轴对称点Q的坐标.
【答案与解析】
解:(1)设二次函数的解析式为y=a(x-2)2+1, 将点O(0,0)的坐标代入得:4a+1=0, 解得a=-. 所以二次函数的解析式为y=-(x-2)2+1; (2)∵抛物线y=-(x-2)2+1的对称轴为直线x=2,且经过原点O(0,0), ∴与x轴的另一个交点B的坐标为(4,0), ∴S△AOB =×4×1=2; (3)∵点P(m,-m)(m≠0)为抛物线y=-(x-2)2+1上一点, ∴-m=-(m-2)2+1, 解得m1=0(舍去),m2=8, ∴P点坐标为(8,-8), ∵抛物线对称轴为直线x=2, ∴P关于抛物线对称轴对称的点Q的坐标为(-4,-8).如下图.
/
【总结升华】考查了运用待定系数法求二次函数的解析式,三角形的面积,二次函数的性质,难度适中.充分利用抛物线的对称性是解题的关键.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(基础)
【巩固练习】
一、选择题 1.抛物线/的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.函数y=/x2+2x+1写成y=a(x-h)2+k的形式是( )
A.y=/(x-1)2+2 B.y=/(x-1)2+/ C.y=/(x-1)2-3 D.y=/(x+2)2-1
3.抛物线y=/x2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( )
A.y=/(x+3)2-2 B.y=/(x-3)2+2 C.y=/(x-3)2-2 D.y=/(x+3)2+2
4.把二次函数/配方成顶点式为( )
A./ B. / C./ D./
5.由二次函数/,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线/
C.其最小值为1 D.当/时,y随x的增大而增大
6.(2019?泰安)在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( ).
A. / B. / C. / D. /
二、填空题
7. 抛物线y=-/(x+3)2-5的开口向_______,对称轴是________,顶点坐标是_______.
8.已知抛物线y=-2(x+1)2-3,如果y随x的增大而减小,那么x的取值范围是_ _____.
9.(2019?宝山区一模)抛物线y=﹣2(x﹣3)2+4的顶点坐标是 .
10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
11.将抛物线/向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.
12.抛物线/的顶点为C,已知/的图象经过点C,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.
三、解答题
13.(2019?盐城校级期末)已知二次函数y=(x﹣2)2﹣4.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,直接写出当y<0时x的取值范围.
14. 已知抛物线/向上平移2个单位长度,再向右平移1个单位长度得到
抛物线/;
(1)求出a,h,k的值;
(2)在同一直角坐标系中,画出/与/的图象;
(3)观察/的图象,当/________时,y随x的增大而增大;
当/________时,函数y有最________值,最________值是/________;
(4)观察/的图象,你能说出对于一切/的值,函数y的取值范围吗?
15.已知抛物线/的顶点为A,原点为O,该抛物线交y轴正半轴于点B,且/,求:(1)此抛物线所对应的函数关系式;
(2)x为何值时,y随x增大而减小?
【答案与解析】
一、选择题 1.【答案】D;
【解析】由顶点式可求顶点,由/得/,此时,/.
2.【答案】D;
【解析】通过配方即可得到结论.
3.【答案】A;
【解析】抛物线 y=/x2向左平移3个单位得到y=/(x+3)2,再向下平移2个单位后,
所得的抛物线表达式是y=/(x+3)2-2.
4.【答案】B;
【解析】通过配方即可得到结论.
5.【答案】C;
【解析】可画草图进行判断.
6.【答案】D;
【解析】解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;
B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;
C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;
D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,
故选D.
二、填空题
7.【答案】下; 直线x=-3 ;(-3,-5);
【解析】由二次函数/的图象性质可得结论.
8.【答案】x≥-1;
【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y随x的增大而减小,
故x≥-1.
9.【答案】(3,4).
【解析】y=﹣2(x﹣3)2+4是抛物线的顶点式,根据顶点式的坐标特点可知,顶点坐标为(3,4).
10.【答案】/;
【解析】设/过点(1,-14)得/,所以/.
11.【答案】/;
【解析】先化一般式为顶点式,再根据平移规律求解.
12.【答案】 1;
【解析】C(2,-6),可求/与x轴交于/,与y轴交于(0,3),∴ /.
三、解答题
/
13.【答案与解析】
解:(1)列表:
x
…
0
1
2
3
4
…
y
…
0
﹣3
﹣4
﹣3
0
…
描点、连线如图;
/
(2)由图象可知:当y<0时x的取值范围是0<x<4.
14.【答案与解析】
(1)由/向上平移2个单位,再向右平移1个单位所得到的抛物线是/.
∴ /,/,/.
(2)函数/与/的图象如图所示.
/
(3)观察/的图象,当/时,/随x的增大而增大;
当/时,函数/有最大值,最大值是/.
(4)由图象知,对于一切/的值,总有函数值/.
15.【答案与解析】
(1)由题意知A(2,1),令/,则/,所以/.
由/得/,所以/,因此抛物线的解析式为/.
(2)当/时,y随x增大而减小.
【学习目标】
1.会用描点法画出二次函数/(a、h、k常数,a≠0)的图象.掌握抛物线/与/图象之间的关系;
2.熟练掌握函数/的有关性质,并能用函数/的性质解决一些实际问题;
3.经历探索/的图象及性质的过程,体验/与/、/、/之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
/的符号
开口方向
顶点坐标
对称轴
性质
/
向上
/
x=h
/时,/随/的增大而增大;/时,/随/的增大而减小;/时,/有最小值/.
/
向下
/
x=h
/时,/随/的增大而减小;/时,/随/的增大而增大;/时,/有最大值/.
2.函数的图象与性质
/的符号
开口方向
顶点坐标
对称轴
性质
/
向上
/
x=h
/时,/随/的增大而增大;/时,/随/的增大而减小;/时,/有最小值/.
/
向下
/
x=h
/时,/随/的增大而减小;/时,/随/的增大而增大;/时,/有最大值/.
要点诠释:
二次函数/的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式/,确定其顶点坐标/;
⑵ 保持抛物线/的形状不变,将其顶点平移到/处,具体平移方法如下:
/
2.平移规律:
在原有函数的基础上“/值正右移,负左移;/值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴/沿/轴平移:向上(下)平移/个单位,/变成
/(或/)
⑵/沿x轴平移:向左(右)平移/个单位,/变成/(或/)
【典型例题】
类型一、二次函数图象及性质
/1.(2019?潮南区模拟)二次函数y=﹣(x﹣3)2+2的顶点的坐标是 ,对称轴是 .
【思路点拨】根据二次函数顶点式解析式分别解答即可.
【答案】(3,2),直线x=3.
【解析】
二次函数y=﹣(x﹣3)2+2;
顶点坐标是(3,2),对称轴是直线x=3.
故答案为:(3,2),直线x=3.
【总结升华】本题考查了二次函数的性质,熟练掌握利用二次函数顶点式形式求解对称轴和顶点坐标的方法是解题的关键.
举一反三:
【 函数与函数的图象与性质 练习2】
【变式】(2019?荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
【答案与解析】
解:y=x2﹣6x+5=(x﹣3)2﹣4,
∴抛物线的顶点坐标为(3,﹣4),
把点(3,﹣4)向上平移2个单位长度,再向右平移1个单位长度得到点的坐标为(4,﹣2),
∴平移后得到的抛物线解析式为y=(x﹣4)2﹣2.
/2.把抛物线/向上平移2个单位,再向左平移4个单位,得到抛物线/,
求b,c的值. 【答案与解析】
根据题意得,y=(x-4)2-2=x2-8x+14, 所以 / 【总结升华】把抛物线/向上平移2个单位,再向左平移4个单位,得到抛物线/,
也就意味着把抛物线/向下平移2个单位,再向右平移4个单位,得到抛物线/.
举一反三:
【变式】二次函数/的图象可以看作是二次函数/的图象向 平移4个单位,再向 平移3个单位得到的.
【答案】上;右.
类型二、二次函数性质的综合应用
/3.(2019秋?安顺期末)二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
/
【答案与解析】
解:(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a=﹣/,
∴二次函数解析式为y1=﹣/(x﹣2)2=﹣/a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:/,
解得:k=/,b=﹣1,
则直线AB解析式为y=/x﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
【总结升华】可先由待定系数法建立方程组求出两个函数的解析式,然后利用函数图象写出自变量的取值范围.
/4.如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B. (1)求抛物线的解析式; (2)求△AOB的面积; (3)若点P(m,-m)(m≠0)为抛物线上一点,求与P关于抛物线对称轴对称的点Q的
坐标.(注:抛物线y=ax2+bx+c的对称轴是x=-).
/
【思路点拨】(1)已知抛物线的顶点为A(2,1),设抛物线为顶点式y=a(x-h)2+k,把点O(0,0)代入即可求解析式; (2)由抛物线的对称轴为直线x=2,且经过原点O(0,0),根据对称性得出与x轴的另一个交点B的坐标,再根据三角形的面积公式即可求出△AOB的面积; (3)将点P(m,-m)代入y=-(x-2)2+1,得出-m=-(m-2)2+1,解方程求出m的值,得到P点坐标,再根据对称性即可求出P关于抛物线对称轴对称点Q的坐标.
【答案与解析】
解:(1)设二次函数的解析式为y=a(x-2)2+1, 将点O(0,0)的坐标代入得:4a+1=0, 解得a=-. 所以二次函数的解析式为y=-(x-2)2+1; (2)∵抛物线y=-(x-2)2+1的对称轴为直线x=2,且经过原点O(0,0), ∴与x轴的另一个交点B的坐标为(4,0), ∴S△AOB =×4×1=2; (3)∵点P(m,-m)(m≠0)为抛物线y=-(x-2)2+1上一点, ∴-m=-(m-2)2+1, 解得m1=0(舍去),m2=8, ∴P点坐标为(8,-8), ∵抛物线对称轴为直线x=2, ∴P关于抛物线对称轴对称的点Q的坐标为(-4,-8).如下图.
/
【总结升华】考查了运用待定系数法求二次函数的解析式,三角形的面积,二次函数的性质,难度适中.充分利用抛物线的对称性是解题的关键.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(基础)
【巩固练习】
一、选择题 1.抛物线/的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.函数y=/x2+2x+1写成y=a(x-h)2+k的形式是( )
A.y=/(x-1)2+2 B.y=/(x-1)2+/ C.y=/(x-1)2-3 D.y=/(x+2)2-1
3.抛物线y=/x2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( )
A.y=/(x+3)2-2 B.y=/(x-3)2+2 C.y=/(x-3)2-2 D.y=/(x+3)2+2
4.把二次函数/配方成顶点式为( )
A./ B. / C./ D./
5.由二次函数/,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线/
C.其最小值为1 D.当/时,y随x的增大而增大
6.(2019?泰安)在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( ).
A. / B. / C. / D. /
二、填空题
7. 抛物线y=-/(x+3)2-5的开口向_______,对称轴是________,顶点坐标是_______.
8.已知抛物线y=-2(x+1)2-3,如果y随x的增大而减小,那么x的取值范围是_ _____.
9.(2019?宝山区一模)抛物线y=﹣2(x﹣3)2+4的顶点坐标是 .
10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
11.将抛物线/向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.
12.抛物线/的顶点为C,已知/的图象经过点C,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.
三、解答题
13.(2019?盐城校级期末)已知二次函数y=(x﹣2)2﹣4.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,直接写出当y<0时x的取值范围.
14. 已知抛物线/向上平移2个单位长度,再向右平移1个单位长度得到
抛物线/;
(1)求出a,h,k的值;
(2)在同一直角坐标系中,画出/与/的图象;
(3)观察/的图象,当/________时,y随x的增大而增大;
当/________时,函数y有最________值,最________值是/________;
(4)观察/的图象,你能说出对于一切/的值,函数y的取值范围吗?
15.已知抛物线/的顶点为A,原点为O,该抛物线交y轴正半轴于点B,且/,求:(1)此抛物线所对应的函数关系式;
(2)x为何值时,y随x增大而减小?
【答案与解析】
一、选择题 1.【答案】D;
【解析】由顶点式可求顶点,由/得/,此时,/.
2.【答案】D;
【解析】通过配方即可得到结论.
3.【答案】A;
【解析】抛物线 y=/x2向左平移3个单位得到y=/(x+3)2,再向下平移2个单位后,
所得的抛物线表达式是y=/(x+3)2-2.
4.【答案】B;
【解析】通过配方即可得到结论.
5.【答案】C;
【解析】可画草图进行判断.
6.【答案】D;
【解析】解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;
B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;
C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;
D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,
故选D.
二、填空题
7.【答案】下; 直线x=-3 ;(-3,-5);
【解析】由二次函数/的图象性质可得结论.
8.【答案】x≥-1;
【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y随x的增大而减小,
故x≥-1.
9.【答案】(3,4).
【解析】y=﹣2(x﹣3)2+4是抛物线的顶点式,根据顶点式的坐标特点可知,顶点坐标为(3,4).
10.【答案】/;
【解析】设/过点(1,-14)得/,所以/.
11.【答案】/;
【解析】先化一般式为顶点式,再根据平移规律求解.
12.【答案】 1;
【解析】C(2,-6),可求/与x轴交于/,与y轴交于(0,3),∴ /.
三、解答题
/
13.【答案与解析】
解:(1)列表:
x
…
0
1
2
3
4
…
y
…
0
﹣3
﹣4
﹣3
0
…
描点、连线如图;
/
(2)由图象可知:当y<0时x的取值范围是0<x<4.
14.【答案与解析】
(1)由/向上平移2个单位,再向右平移1个单位所得到的抛物线是/.
∴ /,/,/.
(2)函数/与/的图象如图所示.
/
(3)观察/的图象,当/时,/随x的增大而增大;
当/时,函数/有最大值,最大值是/.
(4)由图象知,对于一切/的值,总有函数值/.
15.【答案与解析】
(1)由题意知A(2,1),令/,则/,所以/.
由/得/,所以/,因此抛物线的解析式为/.
(2)当/时,y随x增大而减小.
同课章节目录
