高一数学人教版必修一2.3幂函数课件(共16张PPT)
文档属性
| 名称 | 高一数学人教版必修一2.3幂函数课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 694.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 14:35:20 | ||
图片预览






文档简介
(共16张PPT)
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
定义域:
值域:
奇偶性:
在R上是增函数
在R上是减函数
单调性:
R
非奇非偶函数
定点:
过点(0,1)
底数越大,向上的方向越靠近y轴
图
象
性
质
定义域:
R
值域:
奇偶性:
非奇非偶函数
定点:
过点(0,1)
单调性:
底数越小,向上的方向越靠近y轴
前提测评
图
象
性
质
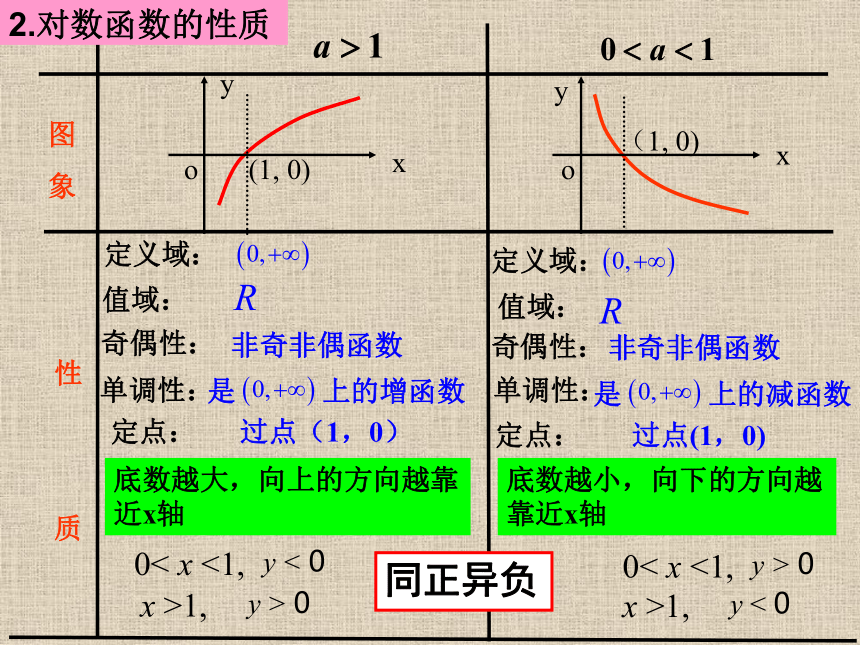
x
y
o
(1,
0)
x
y
o
(1,
0)
定义域:
值域:
奇偶性:
单调性:
定点:
过点(1,0)
定义域:
值域:
奇偶性:
定点:
过点(1,0)
单调性:
非奇非偶函数
非奇非偶函数
是
上的增函数
是
上的减函数
底数越大,向上的方向越靠近x轴
底数越小,向下的方向越靠近x轴
y
<
0
0<
x
<1,
x
>1,
y
>
0
y
>
0
0<
x
<1,
x
>1,
y
<
0
同正异负
2.对数函数的性质
展示目标
(1)知识目标:
掌握幂函数函数的概念、图象和性质;
(2)能力目标:
体会分类思想、数形结合思想;培养分析、比
较、抽象、概括的思维能力;
(3)情感目标:
激发学习数学应用数学的兴趣,培养勇于探索的创新精神
.
导学达标
①
幂函数的定义
通过幂函数的图像归纳总结
函数的性质
思考
问题引入
(1)
如果张红购买了每千克1元的蔬菜w千克,那么她需要支付p=
元
(2)
如果正方形的边长为a,那么正方形的面积
(3)
如果立方体的边长为a,那么立方体的体积
(4)如果一个正方形场地的面积为S,那么这个正方形的边长
(5)如果人t
s内骑车行进了1
km,那么他骑车的平均速度
我们先看几个具体问题:
若将它们的自变量全部用x来表示,函数值用y来表示,则它们的函数关系式将是:
w
说明:
对于幂函数,我们只讨论
=1,2,3,
,-1
时的情形。
①
幂函数的定义
一般地,函数
叫做幂函数,其中x是自变量
,
是常数
例1:
判断下列函数是否为幂函数.
(1)
y=x4
(3)
y=
-x2
(5)
y=2x2
(6)
y=x3+2
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
作出幂函数图象:
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
从图象能得出他们的性质吗
②几个幂函数的性质:
定义域
值域
奇偶性
单调性
定点
R
R
R
R
R
奇函数
奇函数
奇函数
非奇非偶
偶函数
增函数
增函数
增函数
(1,1)
幂函数不同指数函数和对数函数,其定义域
随
的不同而不同。
1、所有幂函数图象都过点
2、
是奇数,则
是奇函数,
是偶数,则
是偶函数。
3、在区间
上,
当
时,
是增函数;
当
时,
是减函数。
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
一般地,幂函数的图象在直线x
=1的右侧,指数大的在上,指数小的在下。
方法技巧:分子有理化
例1.证明幂函数
在
上是增函数
达标测评
课本P79
习题2.3
1,3
家庭作业
课本P83
B组
3
预习§3.1.1
方程的根与函数的零点
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
定义域:
值域:
奇偶性:
在R上是增函数
在R上是减函数
单调性:
R
非奇非偶函数
定点:
过点(0,1)
底数越大,向上的方向越靠近y轴
图
象
性
质
定义域:
R
值域:
奇偶性:
非奇非偶函数
定点:
过点(0,1)
单调性:
底数越小,向上的方向越靠近y轴
前提测评
图
象
性
质
x
y
o
(1,
0)
x
y
o
(1,
0)
定义域:
值域:
奇偶性:
单调性:
定点:
过点(1,0)
定义域:
值域:
奇偶性:
定点:
过点(1,0)
单调性:
非奇非偶函数
非奇非偶函数
是
上的增函数
是
上的减函数
底数越大,向上的方向越靠近x轴
底数越小,向下的方向越靠近x轴
y
<
0
0<
x
<1,
x
>1,
y
>
0
y
>
0
0<
x
<1,
x
>1,
y
<
0
同正异负
2.对数函数的性质
展示目标
(1)知识目标:
掌握幂函数函数的概念、图象和性质;
(2)能力目标:
体会分类思想、数形结合思想;培养分析、比
较、抽象、概括的思维能力;
(3)情感目标:
激发学习数学应用数学的兴趣,培养勇于探索的创新精神
.
导学达标
①
幂函数的定义
通过幂函数的图像归纳总结
函数的性质
思考
问题引入
(1)
如果张红购买了每千克1元的蔬菜w千克,那么她需要支付p=
元
(2)
如果正方形的边长为a,那么正方形的面积
(3)
如果立方体的边长为a,那么立方体的体积
(4)如果一个正方形场地的面积为S,那么这个正方形的边长
(5)如果人t
s内骑车行进了1
km,那么他骑车的平均速度
我们先看几个具体问题:
若将它们的自变量全部用x来表示,函数值用y来表示,则它们的函数关系式将是:
w
说明:
对于幂函数,我们只讨论
=1,2,3,
,-1
时的情形。
①
幂函数的定义
一般地,函数
叫做幂函数,其中x是自变量
,
是常数
例1:
判断下列函数是否为幂函数.
(1)
y=x4
(3)
y=
-x2
(5)
y=2x2
(6)
y=x3+2
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
作出幂函数图象:
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
从图象能得出他们的性质吗
②几个幂函数的性质:
定义域
值域
奇偶性
单调性
定点
R
R
R
R
R
奇函数
奇函数
奇函数
非奇非偶
偶函数
增函数
增函数
增函数
(1,1)
幂函数不同指数函数和对数函数,其定义域
随
的不同而不同。
1、所有幂函数图象都过点
2、
是奇数,则
是奇函数,
是偶数,则
是偶函数。
3、在区间
上,
当
时,
是增函数;
当
时,
是减函数。
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
一般地,幂函数的图象在直线x
=1的右侧,指数大的在上,指数小的在下。
方法技巧:分子有理化
例1.证明幂函数
在
上是增函数
达标测评
课本P79
习题2.3
1,3
家庭作业
课本P83
B组
3
预习§3.1.1
方程的根与函数的零点
