人教A版高中数学必修1课件:3.1.2用二分法求方程的近似解(共31张PPT)
文档属性
| 名称 | 人教A版高中数学必修1课件:3.1.2用二分法求方程的近似解(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 14:45:23 | ||
图片预览










文档简介
(共31张PPT)
CCTV2“幸运52”片段 :
主持人李咏说道:猜一猜这架家用型数码相机的价格.
观众甲:2000!李咏:高了!
观众乙:1000! 李咏:低了!
观众丙:1500! 李咏:还是低了!········
问题1:你知道这件商品的价格在什么范围内吗?
问题2:若接下来让你猜的话,你会猜多少价格比较合理呢?
答案:1500至2000之间
课前活动
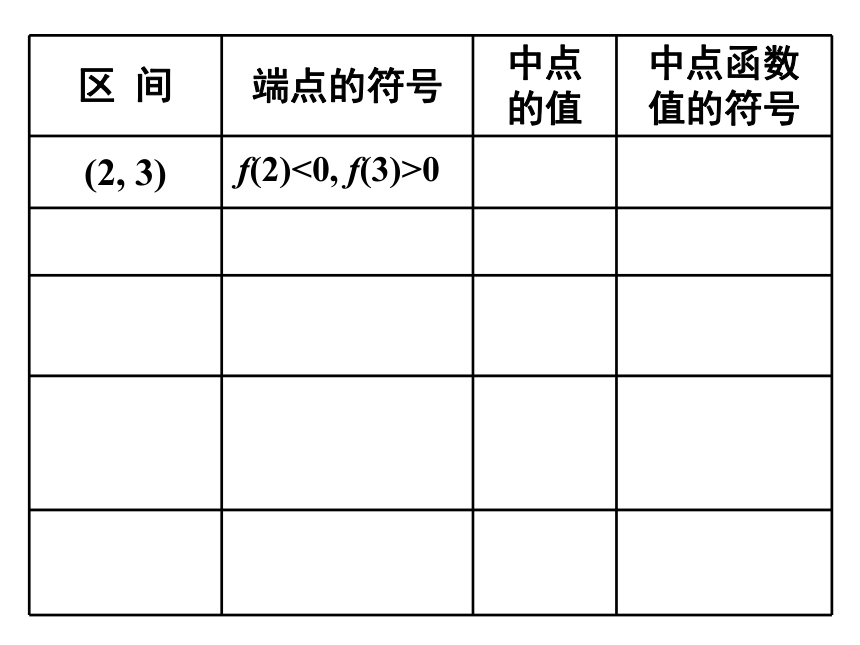
我们已经知道,函数f(x)=lnx+2x-6在区间(2,3)内有零点;如何找到这个零点呢?
如果能够将零点的范围尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.
课前活动
在有限次重复相同的步骤后,在一定的精度下,可以将所得到的零点所在区间上任意的一点(如:端点)作为零点的近似值。
课中活动1
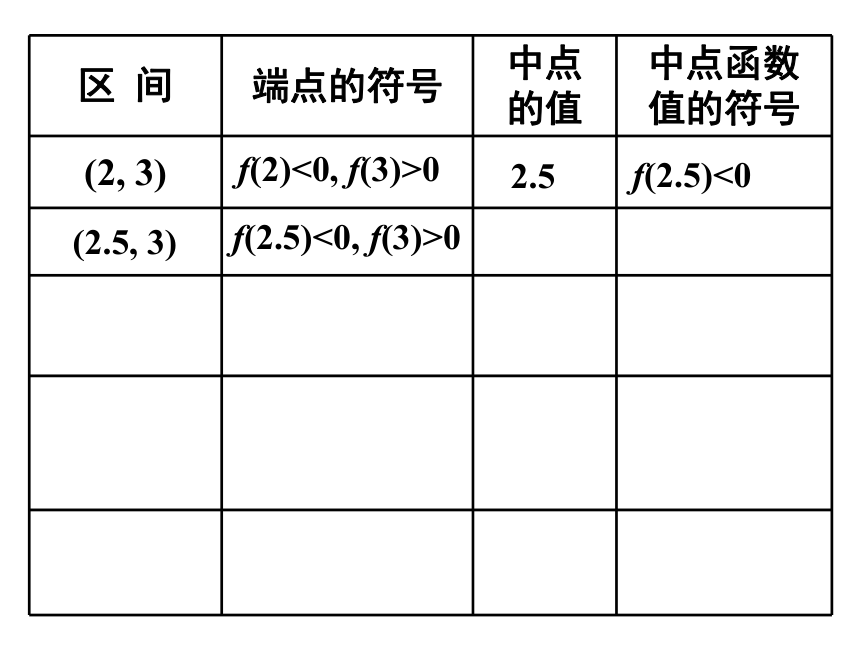
取区间(2,3)的中点2.5,
用计算器算得f(2.5)≈-0.084,因为f(2.5)×f(3)<0,
所以零点在区间(2.5,3)内;
再取区间(2.5,3)的中点2.75,算得f(2.75)≈0.512,
因为f(2.5)×f(2.75)<0,所以零点在(2.5,2.75)内;…
区 间 端点的符号 中点
的值 中点函数
值的符号
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5, 3)
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 2.75)
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5, 2.5625)
f(2.5)<0,
f( 2.5625)>0
2.53125
f(2.53125)<0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
解:观察上表知:0.007813<0.01,
所以x=2.535125或2.5390625为函数
f(x)=lnx+2x-6零点的近似值。
给这种方法取个名字?
区间(a,b) 中点值m f(m)的近似值 精确度|a-b|
(2,3) 2.5 -0.084 1
(2.5,3) 2.75 0.512 0.5
(2.5,2.75) 2.625 0.215 0.25
(2.5,2.625) 2.562 5 0.066 0.125
(2.5,2.562 5) 2.531 25 -0.009 0.0625
(2.531 25,2.562 5) 2.546 875 0.029 0.03125
(2.531 25,2.546 875) 2.539 062 5 0.01 0.015625
(2.531 25,2.539 062 5) 2.535 156 25 0.001 0.007813
对于在区间[a,b]上连续不断且
f (a)·f (b)<0的函数y=f (x),通过不
断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼
近零点,进而得到零点近似值的方
法叫做二分法.
二分法的定义
课中活动1
用二分法求函数f(x)零点近似值的步骤:
例2、借助计算器或计算机用二分法求方程
的近似解(精确到0.1)
分析思考:原方程 的近似解和哪个函数的零点是等价的?
解:原方程即 , 令 , 用计算器或计算机作出函数 的对应值表与图象(如下):
课中活动2
x 0 1 2 3 4 5 6 7
f(x)=2x+3x-7 -6 -2 3 10 21 40 75 142
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口 诀
中值计算两边看;
区间长度缩一半;
精确度上来判断.
用二分法求方程的近似解
课中活动3
P92 1 2
创新设计P52 课堂达标1-5
课 中活动4
小结
1. 二分法的定义;
2. 用二分法求函数零点近似值的步骤.
课 后 活动
完成《创新设计》上这一节的所有题目
CCTV2“幸运52”片段 :
主持人李咏说道:猜一猜这架家用型数码相机的价格.
观众甲:2000!李咏:高了!
观众乙:1000! 李咏:低了!
观众丙:1500! 李咏:还是低了!········
问题1:你知道这件商品的价格在什么范围内吗?
问题2:若接下来让你猜的话,你会猜多少价格比较合理呢?
答案:1500至2000之间
课前活动
我们已经知道,函数f(x)=lnx+2x-6在区间(2,3)内有零点;如何找到这个零点呢?
如果能够将零点的范围尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.
课前活动
在有限次重复相同的步骤后,在一定的精度下,可以将所得到的零点所在区间上任意的一点(如:端点)作为零点的近似值。
课中活动1
取区间(2,3)的中点2.5,
用计算器算得f(2.5)≈-0.084,因为f(2.5)×f(3)<0,
所以零点在区间(2.5,3)内;
再取区间(2.5,3)的中点2.75,算得f(2.75)≈0.512,
因为f(2.5)×f(2.75)<0,所以零点在(2.5,2.75)内;…
区 间 端点的符号 中点
的值 中点函数
值的符号
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 3)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5, 3)
(2.5, 2.75)
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5, 3)
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5, 2.75)
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5, 2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5, 2.5625)
f(2.5)<0,
f( 2.5625)>0
2.53125
f(2.53125)<0
区 间 端点的符号 中点
的值 中点函数
值的符号
(2, 3)
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
(2.53125, 2.5625) f(2.53125)<0,
f(2.5625)>0 2.546875 f(2.546875)
>0
(2.53125,
2.546875) f(2.53125)
<0,
f(2.546875)
>0 2.5390625 f(2.5390625)
>0
(2.53125,
2.5390625) f(2.53125)
<0,
f(2.5390625)
>0 2.53515625 f(2.53515625)
>0
解:观察上表知:0.007813<0.01,
所以x=2.535125或2.5390625为函数
f(x)=lnx+2x-6零点的近似值。
给这种方法取个名字?
区间(a,b) 中点值m f(m)的近似值 精确度|a-b|
(2,3) 2.5 -0.084 1
(2.5,3) 2.75 0.512 0.5
(2.5,2.75) 2.625 0.215 0.25
(2.5,2.625) 2.562 5 0.066 0.125
(2.5,2.562 5) 2.531 25 -0.009 0.0625
(2.531 25,2.562 5) 2.546 875 0.029 0.03125
(2.531 25,2.546 875) 2.539 062 5 0.01 0.015625
(2.531 25,2.539 062 5) 2.535 156 25 0.001 0.007813
对于在区间[a,b]上连续不断且
f (a)·f (b)<0的函数y=f (x),通过不
断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼
近零点,进而得到零点近似值的方
法叫做二分法.
二分法的定义
课中活动1
用二分法求函数f(x)零点近似值的步骤:
例2、借助计算器或计算机用二分法求方程
的近似解(精确到0.1)
分析思考:原方程 的近似解和哪个函数的零点是等价的?
解:原方程即 , 令 , 用计算器或计算机作出函数 的对应值表与图象(如下):
课中活动2
x 0 1 2 3 4 5 6 7
f(x)=2x+3x-7 -6 -2 3 10 21 40 75 142
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口 诀
中值计算两边看;
区间长度缩一半;
精确度上来判断.
用二分法求方程的近似解
课中活动3
P92 1 2
创新设计P52 课堂达标1-5
课 中活动4
小结
1. 二分法的定义;
2. 用二分法求函数零点近似值的步骤.
课 后 活动
完成《创新设计》上这一节的所有题目
