人教A版高中数学必修1课件:3.1.1方程的根与函数的零点(共15张PPT)
文档属性
| 名称 | 人教A版高中数学必修1课件:3.1.1方程的根与函数的零点(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 14:56:28 | ||
图片预览



文档简介
(共15张PPT)
课前活动
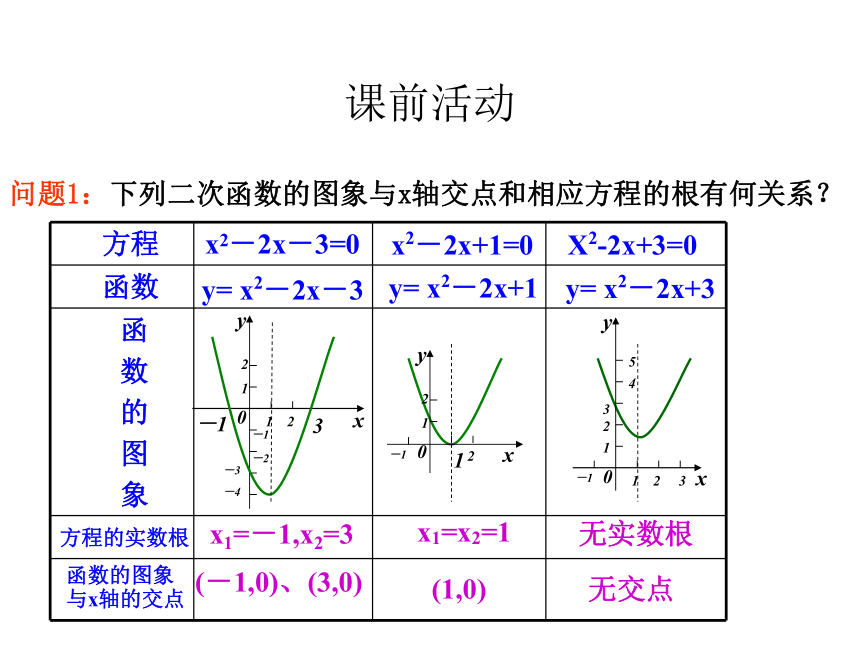
问题1:下列二次函数的图象与x轴交点和相应方程的根有何关系?
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
课前活动
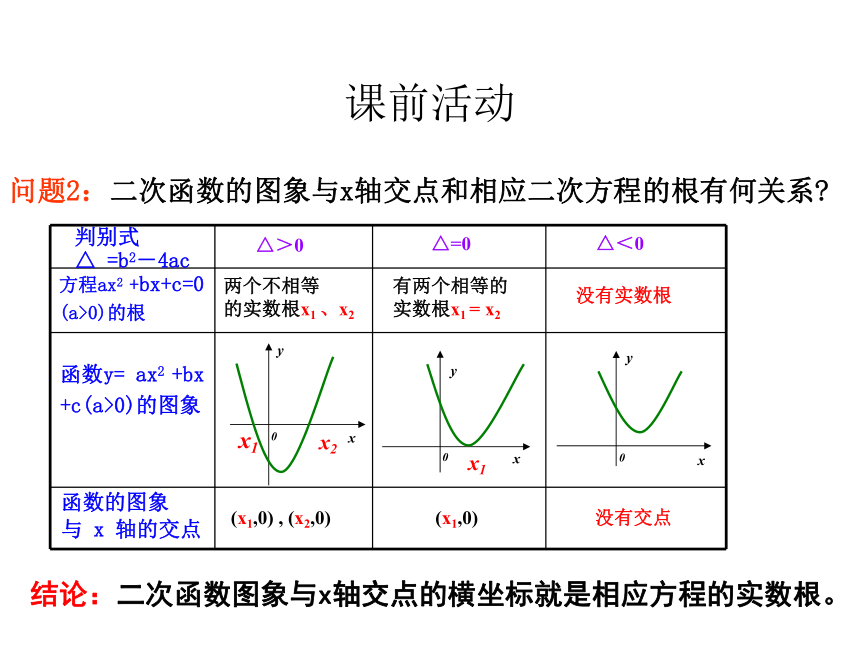
问题2:二次函数的图象与x轴交点和相应二次方程的根有何关系?
方程ax2 +bx+c=0
(a>0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
没有实数根
结论:二次函数图象与x轴交点的横坐标就是相应方程的实数根。
课中活动
一、函数零点的定义
对于函数y=f(x),我们把使f(x)=0的实数x
叫作函数y=f(x)的零点(zero point).
特别注意:零点不是点,零点是实数
课中活动
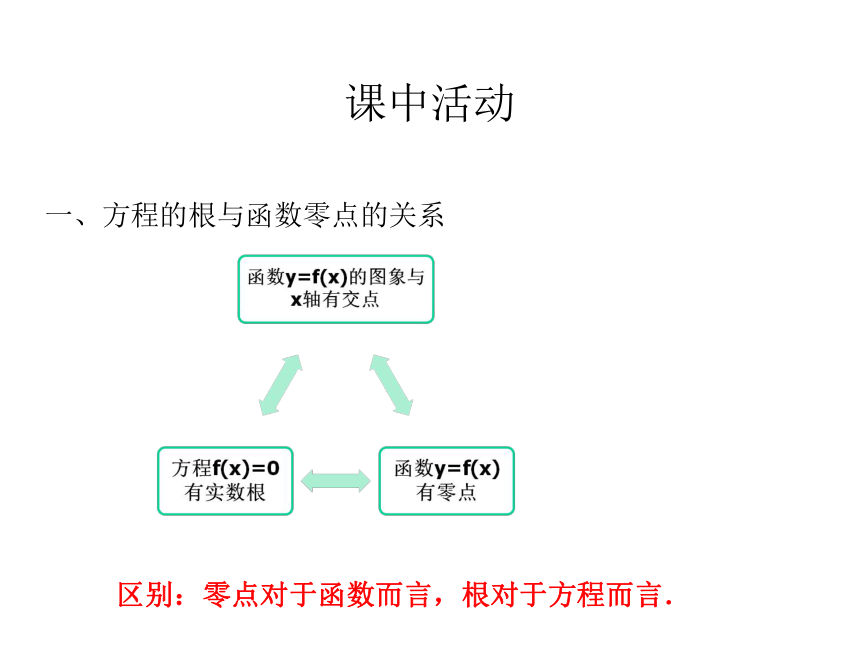
一、方程的根与函数零点的关系
区别:零点对于函数而言,根对于方程而言.
课中活动
例1、求下列函数的零点
归纳:求零点的方法
(1)方程法 (2)图象法
课中活动
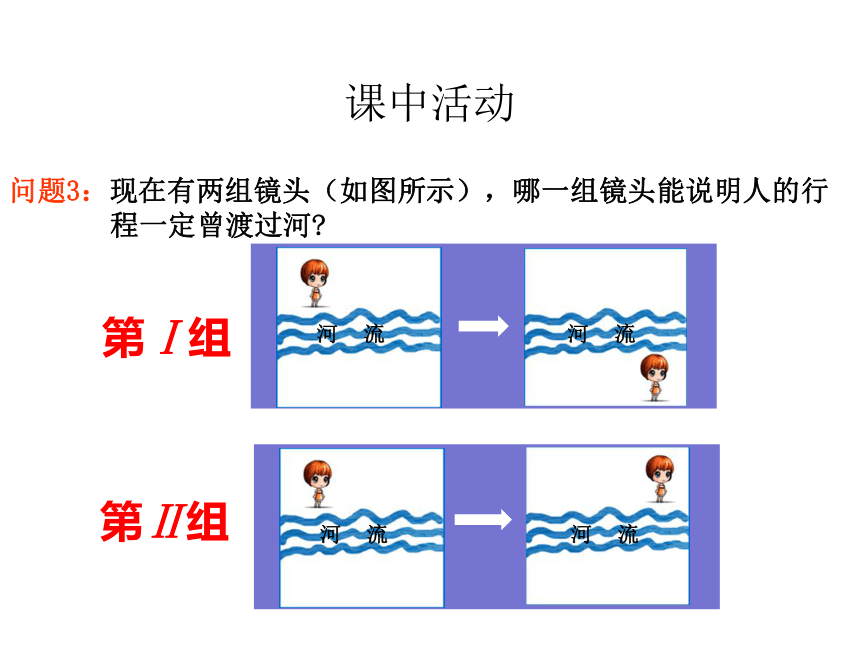
问题3:现在有两组镜头(如图所示),哪一组镜头能说明人的行程一定曾渡过河?
第Ⅰ组
第Ⅱ组
课中活动
问题3:将河流抽象成x轴,将前后的两个位置视为A、B两点。请问当A、B与x轴怎样的位置关系时,AB间的一段连续不断的函数图象与x轴一定会有交点?
x
问题4:A、B与x轴的位置关系,如何用数学符号(式子)来表示?
a
b
课中活动
二、函数零点的存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.即存在c∈(a,b),使得f(c)=0,这个c也就方程f(x)=0的根.
3.1.1方程的根与函数的零点
辨析1:若函数y=f(x)在区间[a,b]上不连续,但f(a)·f(b)<0,则f(x)在区间(a,b)内一定有零点么?
(不一定)
辨析2:若函数y=f(x)在区间[a,b]上连续,但f(a)·f(b)>0,则f(x)在区间(a,b)内一定没有零点么?
(不一定)
辨析3:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内一定只有一个零点么?
(不一定,有几个零点不确定)
思考:增加什么条件时,函数在区间(a,b)上只有一个零点?
(单调)
推论:在零点存在的条件下,如果函数在[a , b]上具有单调性,函数f(x)在区间(a , b)上可存在唯一零点。
课中活动
课中活动
例2、已知函数f(x)的图像是连续不断的,且有如下对应值表:
问:那么函数在区间[1 , 6]上的零点至少有几个,哪些区间上一定存在零点
答案:至少有3个零点
分别在区间 (2, 3),(3,4),(4,5)上
X 1 2 3 4 5 6
f(x) 23 9 -7 11 -5 -12
课中活动
由表和图可知
f(2)<0,f(3)>0,
即f(2)·f(3)<0,
说明这个函数在区间(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点。
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
例3:求函数f(x)=lnx+2x-6的零点个数。
(函数的部分取值和函数图象已给出 )
x 1 2 3 4 5 6 7 8 9
f(x)
课中活动
归纳总结,提高认识
1.函数零点的定义
2.函数的零点与方程的根的等价关系
3.函数零点的存在性定理
课后活动
布置作业
《创新设计》P49上的题目。
课前活动
问题1:下列二次函数的图象与x轴交点和相应方程的根有何关系?
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
课前活动
问题2:二次函数的图象与x轴交点和相应二次方程的根有何关系?
方程ax2 +bx+c=0
(a>0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
没有实数根
结论:二次函数图象与x轴交点的横坐标就是相应方程的实数根。
课中活动
一、函数零点的定义
对于函数y=f(x),我们把使f(x)=0的实数x
叫作函数y=f(x)的零点(zero point).
特别注意:零点不是点,零点是实数
课中活动
一、方程的根与函数零点的关系
区别:零点对于函数而言,根对于方程而言.
课中活动
例1、求下列函数的零点
归纳:求零点的方法
(1)方程法 (2)图象法
课中活动
问题3:现在有两组镜头(如图所示),哪一组镜头能说明人的行程一定曾渡过河?
第Ⅰ组
第Ⅱ组
课中活动
问题3:将河流抽象成x轴,将前后的两个位置视为A、B两点。请问当A、B与x轴怎样的位置关系时,AB间的一段连续不断的函数图象与x轴一定会有交点?
x
问题4:A、B与x轴的位置关系,如何用数学符号(式子)来表示?
a
b
课中活动
二、函数零点的存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.即存在c∈(a,b),使得f(c)=0,这个c也就方程f(x)=0的根.
3.1.1方程的根与函数的零点
辨析1:若函数y=f(x)在区间[a,b]上不连续,但f(a)·f(b)<0,则f(x)在区间(a,b)内一定有零点么?
(不一定)
辨析2:若函数y=f(x)在区间[a,b]上连续,但f(a)·f(b)>0,则f(x)在区间(a,b)内一定没有零点么?
(不一定)
辨析3:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内一定只有一个零点么?
(不一定,有几个零点不确定)
思考:增加什么条件时,函数在区间(a,b)上只有一个零点?
(单调)
推论:在零点存在的条件下,如果函数在[a , b]上具有单调性,函数f(x)在区间(a , b)上可存在唯一零点。
课中活动
课中活动
例2、已知函数f(x)的图像是连续不断的,且有如下对应值表:
问:那么函数在区间[1 , 6]上的零点至少有几个,哪些区间上一定存在零点
答案:至少有3个零点
分别在区间 (2, 3),(3,4),(4,5)上
X 1 2 3 4 5 6
f(x) 23 9 -7 11 -5 -12
课中活动
由表和图可知
f(2)<0,f(3)>0,
即f(2)·f(3)<0,
说明这个函数在区间(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点。
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
例3:求函数f(x)=lnx+2x-6的零点个数。
(函数的部分取值和函数图象已给出 )
x 1 2 3 4 5 6 7 8 9
f(x)
课中活动
归纳总结,提高认识
1.函数零点的定义
2.函数的零点与方程的根的等价关系
3.函数零点的存在性定理
课后活动
布置作业
《创新设计》P49上的题目。
