人教A版高中数学必修1课件:1.3.2奇偶性(共20张PPT)
文档属性
| 名称 | 人教A版高中数学必修1课件:1.3.2奇偶性(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 17:30:40 | ||
图片预览





文档简介
(共21张PPT)
请
你
欣
赏
请
你
欣
赏
请
你
欣
赏
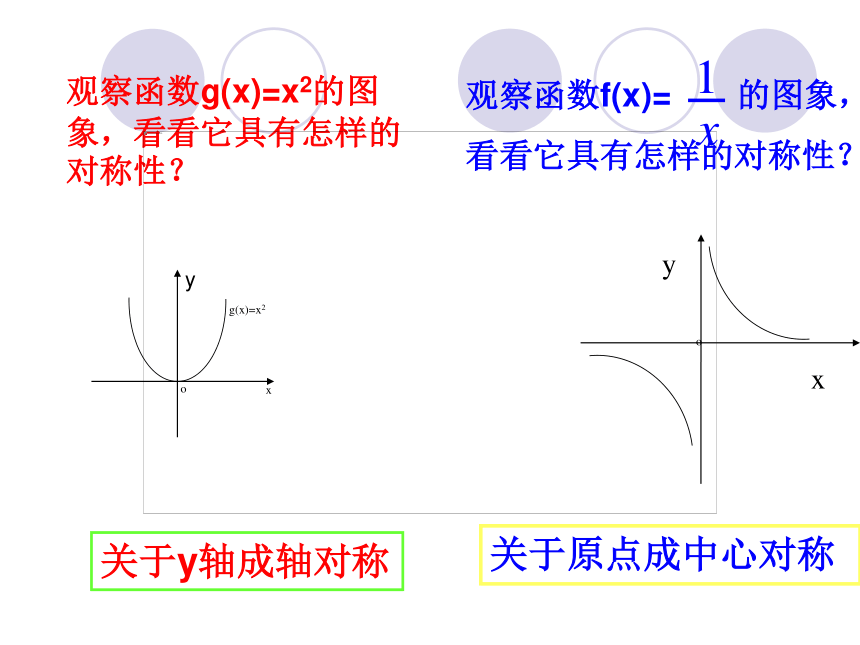
观察函数g(x)=x2的图象,看看它具有怎样的对称性?
关于y轴成轴对称
o
x
y
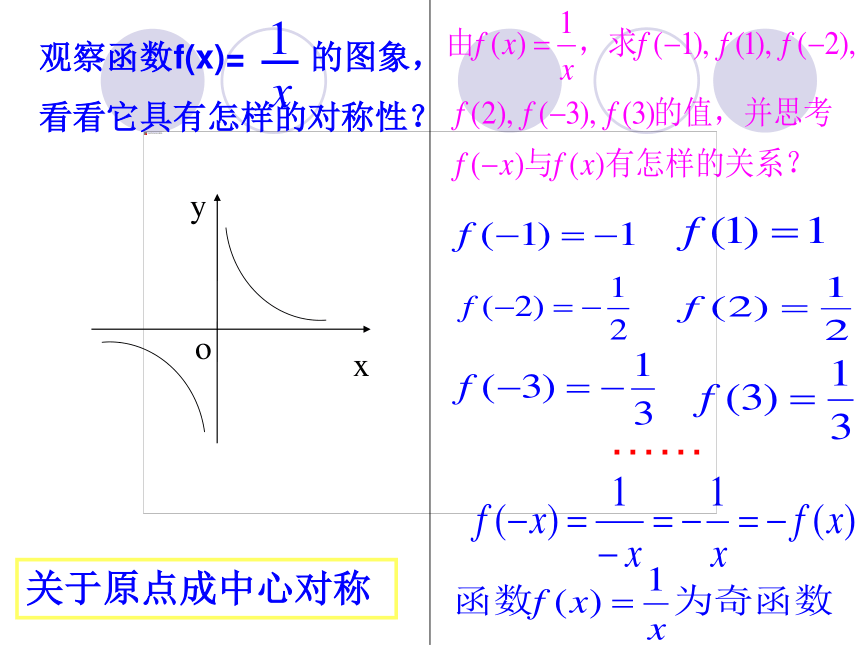
关于原点成中心对称
观察函数g(x)=x2的图象,看看它具有怎样的对称性?
关于y轴成轴对称
由g(x)=x2求g(-1)、 g(1)、 g(-2)、 g(2)、 g(-3)、 g(3)的值,并思考g(-x) 与g(x)有怎样的关系?
g(-1)= (-1)2=1
g(1) =12=1
g(-2)= (-2)2=4、
g(-3)= (-3)2=9、
g(3) = 32 =9、
g(-x) =(-x)2=x2=g(x)
函数 g(x)=x2 为偶函数
……
g(2)= 22=4、
新课教学
(一)函数的奇偶性定义
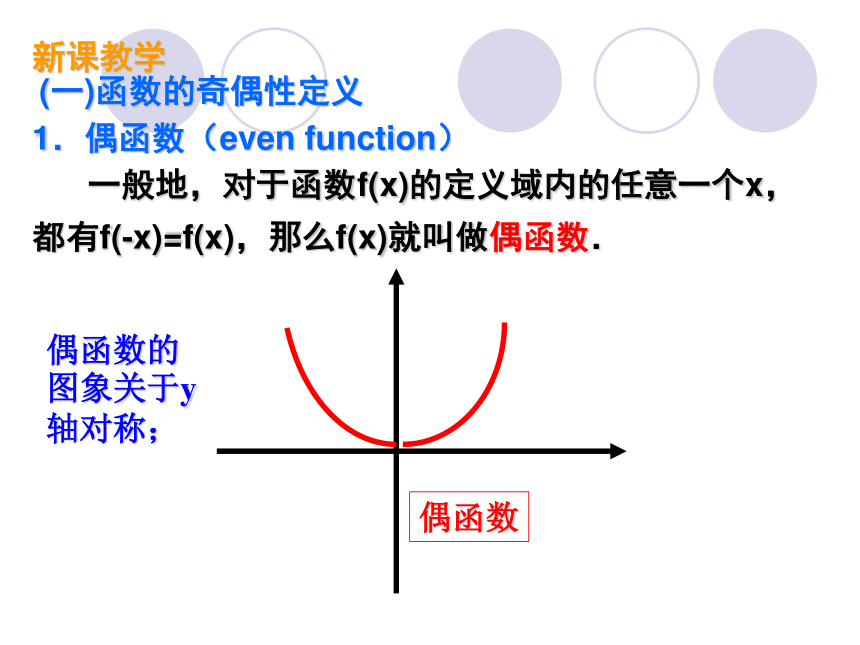
1.偶函数(even function)
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
偶函数
偶函数的图象关于y轴对称;
……
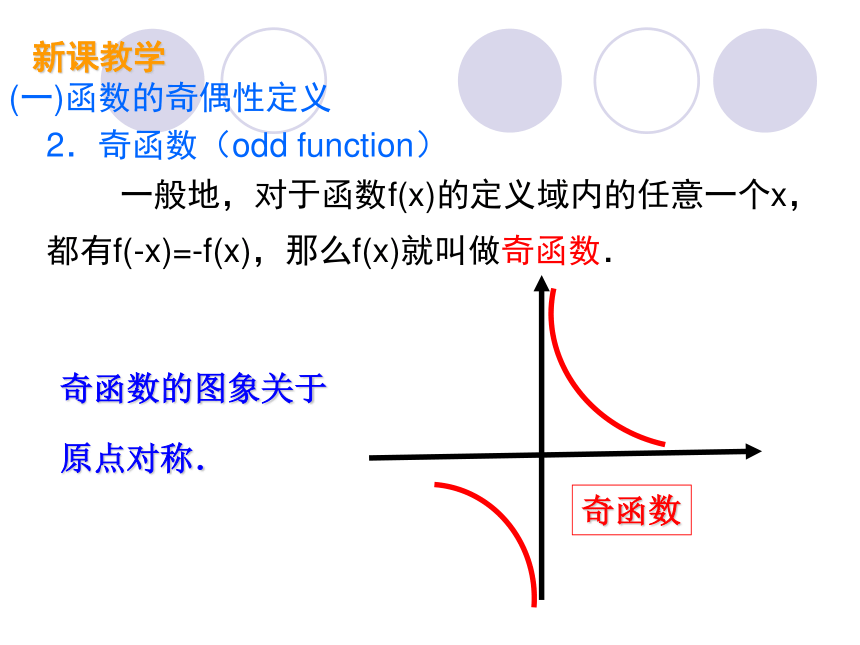
2.奇函数(odd function)
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.
新课教学
(一)函数的奇偶性定义
奇函数
奇函数的图象关于原点对称.
(二)具有奇偶性的函数的图象的特征:
①偶函数的图象关于y轴对称;
②奇函数的图象关于原点对称.
注意:
①函数是奇函数或是偶函数称为函数的奇偶性,
函数的奇偶性是函数的整体性质;
②由函数的奇偶性定义可知,函数具有奇偶性
的一个必要条件是,对于定义域内的任意一个x,
则-x也一定是定义域内的一个自变量(即定义域
关于原点对称).
新课教学
(三)典型例题
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
总结:利用定义判断函数奇偶性的格式步骤:
①首先确定函数的定义域,并判断其定义域是否
关于原点对称;
②确定f(-x)与f(x)的关系;
③作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,
则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,
则f(x)是奇函数.
练习:判断下列函数的奇偶性:
(1) f(x)=x+x3+x5; (2) f(x)=x2+1;
(3) f(x)=x+1 ; (4) f(x)=x2 ,x∈[-1,2]
(5) f(x)=0
利用函数的奇偶性补全函数的图象
练习2:如图是函数 图像的一部分,你
能根据 的奇偶性画出它在y轴左边的图象吗?
解:
∵ 对定义域内的每一个x,都有
奇函数的图象关于原点
对称,因此可以画出函数
的图象:
作业布置
P39 6
B 3
请
你
欣
赏
请
你
欣
赏
请
你
欣
赏
观察函数g(x)=x2的图象,看看它具有怎样的对称性?
关于y轴成轴对称
o
x
y
关于原点成中心对称
观察函数g(x)=x2的图象,看看它具有怎样的对称性?
关于y轴成轴对称
由g(x)=x2求g(-1)、 g(1)、 g(-2)、 g(2)、 g(-3)、 g(3)的值,并思考g(-x) 与g(x)有怎样的关系?
g(-1)= (-1)2=1
g(1) =12=1
g(-2)= (-2)2=4、
g(-3)= (-3)2=9、
g(3) = 32 =9、
g(-x) =(-x)2=x2=g(x)
函数 g(x)=x2 为偶函数
……
g(2)= 22=4、
新课教学
(一)函数的奇偶性定义
1.偶函数(even function)
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
偶函数
偶函数的图象关于y轴对称;
……
2.奇函数(odd function)
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.
新课教学
(一)函数的奇偶性定义
奇函数
奇函数的图象关于原点对称.
(二)具有奇偶性的函数的图象的特征:
①偶函数的图象关于y轴对称;
②奇函数的图象关于原点对称.
注意:
①函数是奇函数或是偶函数称为函数的奇偶性,
函数的奇偶性是函数的整体性质;
②由函数的奇偶性定义可知,函数具有奇偶性
的一个必要条件是,对于定义域内的任意一个x,
则-x也一定是定义域内的一个自变量(即定义域
关于原点对称).
新课教学
(三)典型例题
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
解:
∵ 对定义域内的每一个x,都有
例1.判断下列函数的奇偶性:
总结:利用定义判断函数奇偶性的格式步骤:
①首先确定函数的定义域,并判断其定义域是否
关于原点对称;
②确定f(-x)与f(x)的关系;
③作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,
则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,
则f(x)是奇函数.
练习:判断下列函数的奇偶性:
(1) f(x)=x+x3+x5; (2) f(x)=x2+1;
(3) f(x)=x+1 ; (4) f(x)=x2 ,x∈[-1,2]
(5) f(x)=0
利用函数的奇偶性补全函数的图象
练习2:如图是函数 图像的一部分,你
能根据 的奇偶性画出它在y轴左边的图象吗?
解:
∵ 对定义域内的每一个x,都有
奇函数的图象关于原点
对称,因此可以画出函数
的图象:
作业布置
P39 6
B 3
