四年级下册数学导学案- 三 平行与相交 北京版(表格式)
文档属性
| 名称 | 四年级下册数学导学案- 三 平行与相交 北京版(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 75.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 14:05:45 | ||
图片预览

文档简介
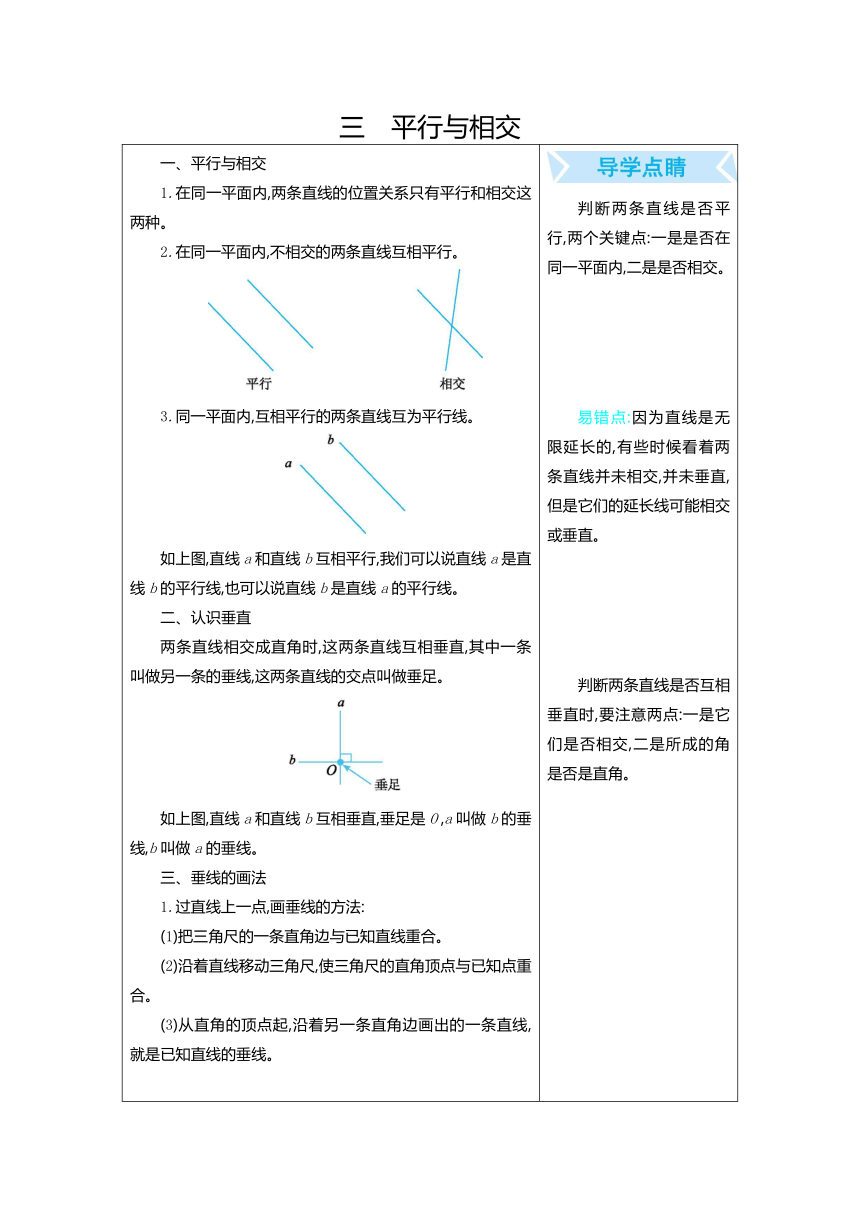
三 平行与相交
一、平行与相交
1.在同一平面内,两条直线的位置关系只有平行和相交这两种。
2.在同一平面内,不相交的两条直线互相平行。
/
3.同一平面内,互相平行的两条直线互为平行线。
/
如上图,直线a和直线b互相平行,我们可以说直线a是直线b的平行线,也可以说直线b是直线a的平行线。
二、认识垂直
两条直线相交成直角时,这两条直线互相垂直,其中一条叫做另一条的垂线,这两条直线的交点叫做垂足。
/
如上图,直线a和直线b互相垂直,垂足是O ,a叫做b的垂线,b叫做a的垂线。
三、垂线的画法
1.过直线上一点,画垂线的方法:
(1)把三角尺的一条直角边与已知直线重合。
(2)沿着直线移动三角尺,使三角尺的直角顶点与已知点重合。
(3)从直角的顶点起,沿着另一条直角边画出的一条直线,就是已知直线的垂线。
/
2.过直线外一点,画垂线的方法:
(1)把三角尺的一条直角边从直线外一点到这条直线所画的与已知直线重合; 垂直线段最短。
(2)沿着直线平移三角尺, 点到直线的距离。使三角尺的另一条直角边和直线外的已知点重合。
(3)沿着另一条直角边画出一条直线。
/
四、平行线的画法
1.将三角尺的斜边与已知直线重合。
2.将直尺与三角尺的一条直角边重合,沿着直尺移动三角尺,直到三角尺的斜边与已知点重合。
3.沿着三角尺的斜边画一条直线。
/
/
判断两条直线是否平行,两个关键点:一是是否在同一平面内,二是是否相交。
易错点:因为直线是无限延长的,有些时候看着两条直线并未相交,并未垂直,但是它们的延长线可能相交或垂直。
判断两条直线是否互相垂直时,要注意两点:一是它们是否相交,二是所成的角是否是直角。
在移动三角尺时,要注意三角尺的一条直角边要始终与已知直线重合。
直线外一点到直线的垂线段,就是点到直线的距离。
直线外一点到已知直线,可以画无数条线段,其中垂线段最短。
两条平行线之间的垂线段都相等。
巧记
同一平面两直线,
如不平行必相交,
相交若是能垂直,
必然形成四直角。
经过线外某个点,
只存一条平行线,
垂线也只有一条,
距离长度是最短。
一、平行与相交
1.在同一平面内,两条直线的位置关系只有平行和相交这两种。
2.在同一平面内,不相交的两条直线互相平行。
/
3.同一平面内,互相平行的两条直线互为平行线。
/
如上图,直线a和直线b互相平行,我们可以说直线a是直线b的平行线,也可以说直线b是直线a的平行线。
二、认识垂直
两条直线相交成直角时,这两条直线互相垂直,其中一条叫做另一条的垂线,这两条直线的交点叫做垂足。
/
如上图,直线a和直线b互相垂直,垂足是O ,a叫做b的垂线,b叫做a的垂线。
三、垂线的画法
1.过直线上一点,画垂线的方法:
(1)把三角尺的一条直角边与已知直线重合。
(2)沿着直线移动三角尺,使三角尺的直角顶点与已知点重合。
(3)从直角的顶点起,沿着另一条直角边画出的一条直线,就是已知直线的垂线。
/
2.过直线外一点,画垂线的方法:
(1)把三角尺的一条直角边从直线外一点到这条直线所画的与已知直线重合; 垂直线段最短。
(2)沿着直线平移三角尺, 点到直线的距离。使三角尺的另一条直角边和直线外的已知点重合。
(3)沿着另一条直角边画出一条直线。
/
四、平行线的画法
1.将三角尺的斜边与已知直线重合。
2.将直尺与三角尺的一条直角边重合,沿着直尺移动三角尺,直到三角尺的斜边与已知点重合。
3.沿着三角尺的斜边画一条直线。
/
/
判断两条直线是否平行,两个关键点:一是是否在同一平面内,二是是否相交。
易错点:因为直线是无限延长的,有些时候看着两条直线并未相交,并未垂直,但是它们的延长线可能相交或垂直。
判断两条直线是否互相垂直时,要注意两点:一是它们是否相交,二是所成的角是否是直角。
在移动三角尺时,要注意三角尺的一条直角边要始终与已知直线重合。
直线外一点到直线的垂线段,就是点到直线的距离。
直线外一点到已知直线,可以画无数条线段,其中垂线段最短。
两条平行线之间的垂线段都相等。
巧记
同一平面两直线,
如不平行必相交,
相交若是能垂直,
必然形成四直角。
经过线外某个点,
只存一条平行线,
垂线也只有一条,
距离长度是最短。
