苏科版2019-2020学年九年级数学下册第五章:二次函数面积系列—最值、定值、等值(扫描版、习题含答案)
文档属性
| 名称 | 苏科版2019-2020学年九年级数学下册第五章:二次函数面积系列—最值、定值、等值(扫描版、习题含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 00:00:00 | ||
图片预览




文档简介
二次函数面积系列—最值、定值、等值
最值问题
最值衍生
定值问题
等值问题
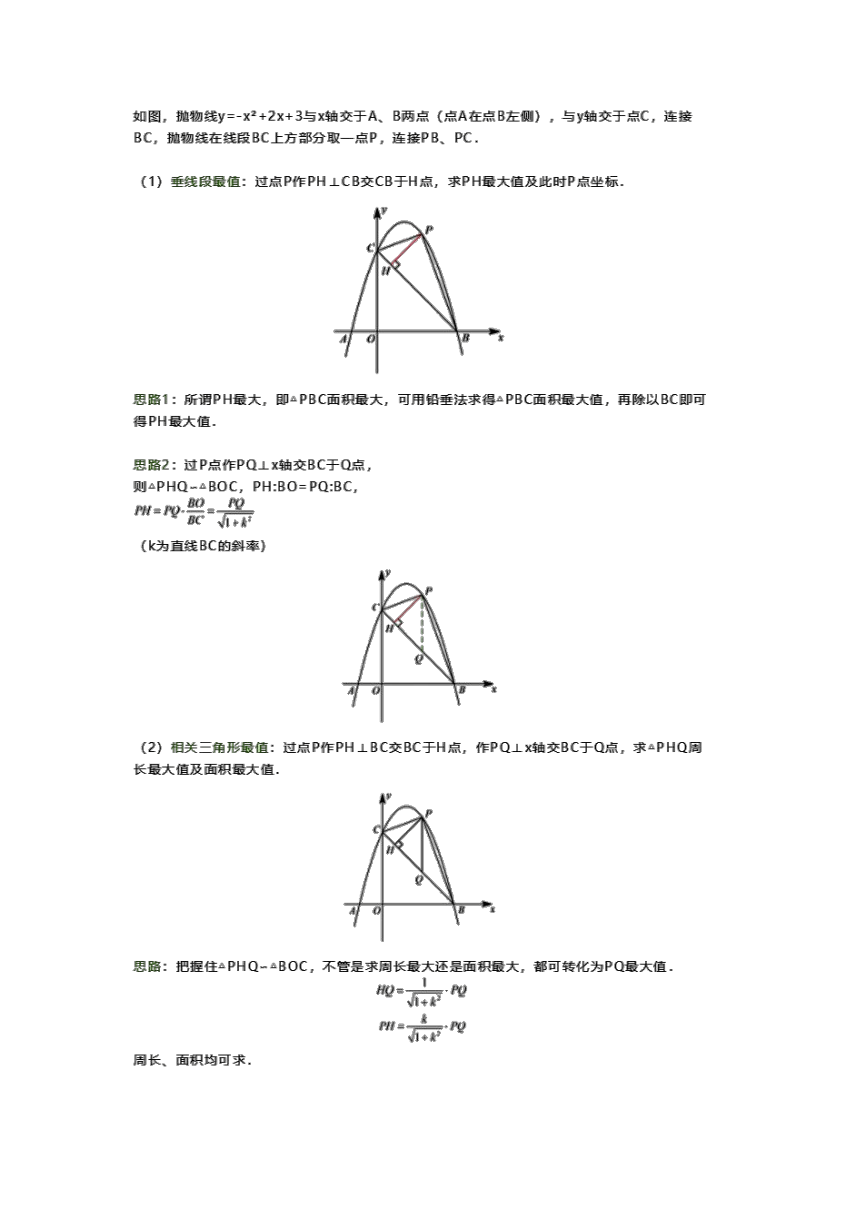
如图,抛物线y=-x2+2X+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,连接
BC,抛物线在线段BC上方部分取一点P,连接PB、PC,使得4PBC面积最大,求面积最大值
及此时P点坐标
【分析】除了上文介绍的铅垂法外,将再介绍一种思路
构造平行切线:以BC为底边,过点P向BC作垂线PH交BC于H点,求4PBC面积最大,在底边
BC确定不变的前提下,PH最大即可
过点P作pQBC,当PQ与抛物线相切时,PQ与BC距离最大,即PH最大
(1)求BC解析式:y=-X+3
据PQⅢBC,可设PQ解析式:y=-x+m
艮据相切,联立方程:x2+2X+3=-X+m,根的判别式为0,可求m
(4)根据P点坐标,即可求得4PBC面积的最大值
但其实即便算出了P点坐标,求4PBC面积也还是要费点事
如图,抛物线y=-x2+2X+3与X轴交于A、B两点(点A在点B左侧),与y轴交于点C,连接
BC,抛物线在线段BC上方部分取一点P,连接PB、P
(1)垂线段最值:过点P作PH⊥CB交CB于H点,求PH最大值及此时P点坐标
思路1:所谓PH最大,即△PBC面积最大,可用铅垂法求得4PBC面积最大值,再除以BC即可
PH最大值
过P点作PQ⊥X轴交BC于Q点
则△PHQ-△BOC,PH:BO=PQ:BC
PH=PC
BO PO
(k为直线BC的斜率)
(2)相关三角形最值:过点P作PH⊥BC交BC于H点,作PQ⊥X轴交BC于Q点,求4PHQ周
长最大值及面积最大值
思路:把握住△PHQ4BOC,不管是求周长最大还是面积最大,都可转化为PQ最大值
PHE
2019聊城中考(删减
如图,在平面直角坐标系中,抛物线y=ax2+bX+C与X轴交于点A(-2,0),点B(4,0),与
轴交于点C(0,8),连接BC,又已知位于y轴右侧且垂直于x轴的动直线,沿x轴正方向从
O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E
(1)求抛物线的表达式
(2)作PF⊥BC,垂足为F,当直线运动时,求Rt-PFD面积的最大值
【分析】
(1)y=-x2+2X+8
(2)根据B、C两点坐标得
直线BC解析式:y=-2X+8
设点P坐标为(m,-m2+2m+8)
则点D坐标为(m,-2m+8)
故线段PD=-m2+2m+8-(-2m+8)=-m2+4m
当m=2时,PD取到最大值4
√5
4√8516
Sm2555
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
