人教A版高中数学必修1课件:1.3.1函数的单调性与最大(小)值(共16张PPT)
文档属性
| 名称 | 人教A版高中数学必修1课件:1.3.1函数的单调性与最大(小)值(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 18:56:43 | ||
图片预览




文档简介
(共16张PPT)
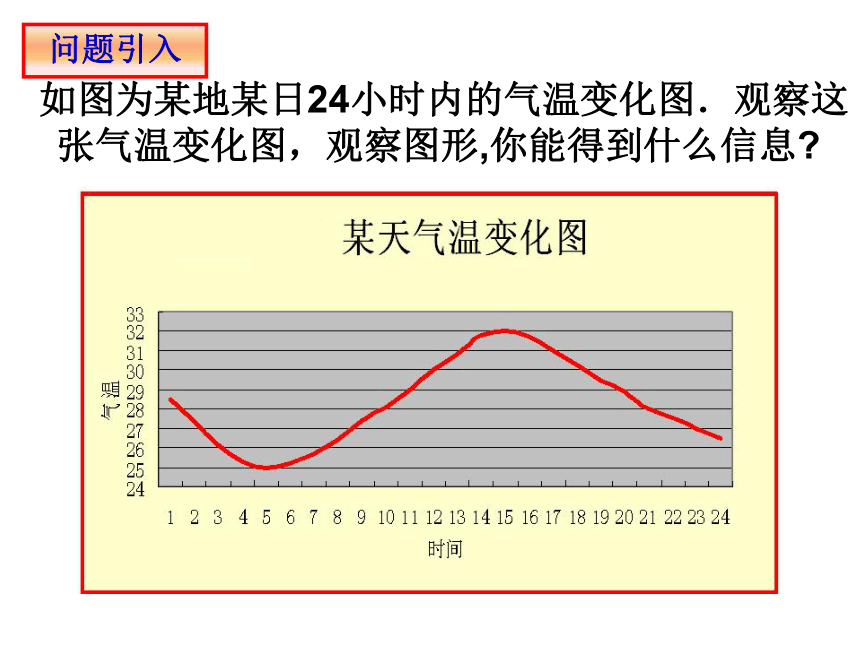
如图为某地某日24小时内的气温变化图.观察这张气温变化图,观察图形,你能得到什么信息?
问题引入
[m,n]上,函数
y 随 x 的增大而减小
在[m,n]上,函数
y 随 x 的增大而增大
——单调递增性
——单调递减性
问题2 能否根据自己的理解说说什么是增函数、减函数?
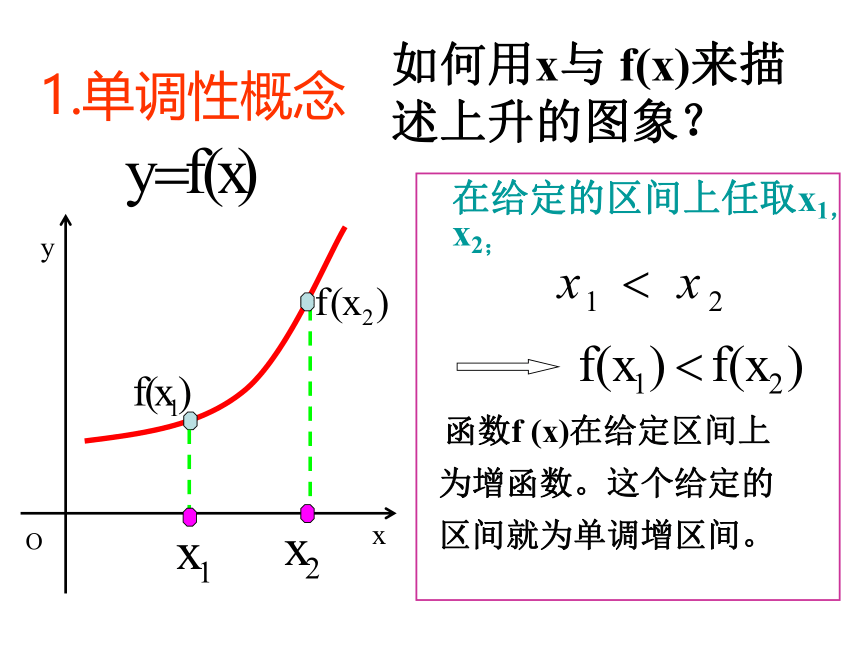
如何用x与 f(x)来描述上升的图象?
1.单调性概念
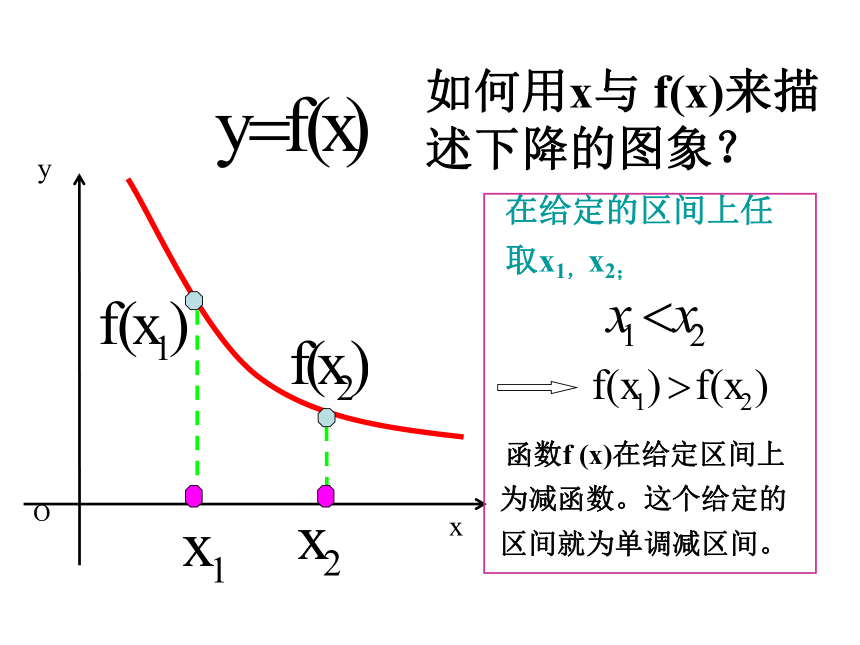
如何用x与 f(x)来描述下降的图象?
例1 下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数?
解:
y=f(x)的单调区间有
[-5,-2),[-2,1)
[1,3),[3,5].
其中y=f(x)在[-5,-2),[1,3)上
是减函数,
在[-2,1), [3,5)上是增函数.
作图是发现函数单调性的方法之一.
2.函数y=x2 是
增函数吗?
是减函数吗?
函数的增减性是针对给定区间来讲的,离开了区间,就不能谈函数的单调性.
利用定义判定(证明)函数的增、减性
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈ (0,+∞)且V10, V2- V1 >0
取值
定号
作差变形
结论
证明步骤:
1.设变量:任取定义域内某区间上的
两变量x1,x2,设x13.定号:判断f(x1) – f(x2)的正、负情况
4.下结论
2. 作差变形
x1
x2
y1
y2
x2
x1
y1
y2
课堂小结:
增函数 减函数
图象
图象特征 自左至右,图象上升. 自左至右,图象下降.
数量 特征 y随x的增大而增大.
当x1<x2时,
f(x1)< f(x2) y随x的增大而减小.
当x1<x2时,
f(x1) > f(x2)
如何根据图象指出(判断)单调区间?
怎样用定义证明函数的单调性?
证明步骤:
1.设变量:任取定义域内某区间上的两变量x1,x2,设x14.下结论
2. 作差变形
3.、定号:判断f(x1) – f(x2)的正、负情况
作业布置
P39 1,2
完成预习案
如图为某地某日24小时内的气温变化图.观察这张气温变化图,观察图形,你能得到什么信息?
问题引入
[m,n]上,函数
y 随 x 的增大而减小
在[m,n]上,函数
y 随 x 的增大而增大
——单调递增性
——单调递减性
问题2 能否根据自己的理解说说什么是增函数、减函数?
如何用x与 f(x)来描述上升的图象?
1.单调性概念
如何用x与 f(x)来描述下降的图象?
例1 下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数?
解:
y=f(x)的单调区间有
[-5,-2),[-2,1)
[1,3),[3,5].
其中y=f(x)在[-5,-2),[1,3)上
是减函数,
在[-2,1), [3,5)上是增函数.
作图是发现函数单调性的方法之一.
2.函数y=x2 是
增函数吗?
是减函数吗?
函数的增减性是针对给定区间来讲的,离开了区间,就不能谈函数的单调性.
利用定义判定(证明)函数的增、减性
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
取值
定号
作差变形
结论
证明步骤:
1.设变量:任取定义域内某区间上的
两变量x1,x2,设x1
4.下结论
2. 作差变形
x1
x2
y1
y2
x2
x1
y1
y2
课堂小结:
增函数 减函数
图象
图象特征 自左至右,图象上升. 自左至右,图象下降.
数量 特征 y随x的增大而增大.
当x1<x2时,
f(x1)< f(x2) y随x的增大而减小.
当x1<x2时,
f(x1) > f(x2)
如何根据图象指出(判断)单调区间?
怎样用定义证明函数的单调性?
证明步骤:
1.设变量:任取定义域内某区间上的两变量x1,x2,设x1
2. 作差变形
3.、定号:判断f(x1) – f(x2)的正、负情况
作业布置
P39 1,2
完成预习案
