人教版八年级数学上册13.3.1等腰三角形中分类讨论课件 (共17张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.1等腰三角形中分类讨论课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 283.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 20:24:47 | ||
图片预览





文档简介
(共17张PPT)
1、△ABC中,AB=AC,∠A=80°,则∠B= °;
2、等腰△ABC中,∠A=80°,则∠B= °;
3、有两边长分别为3cm、5cm的等腰三角形的
周长为 ;
4、等腰三角形的周长为10cm,其中一边长为2cm,
则另两边长为 ;
5、若等腰三角形腰上的高等于腰的一半,则顶角
度数为 ;
6、等腰三角形 、 、
互相重合。
二、关于分类讨论:
(1)定义:当数学问题的条件或结论不确定时就应该分类讨论。分类讨论的基本思想就是指在解决一个问题时,将问题划分成几个能用不同形式去解决的小问题,将这些小问题一一加以解决从而使问题得到解决。
(2)实质:将整体问题化为部分问题来解决。
(3)原则:分类必须不重复、不遗漏并要综合讨论结果。
你的感悟?
三、自主探究,应用分类:
(1)关于边的分类:已知实数x、y满足
+ =0,则以x、y的值为两边长的等腰三角形的周长为多少?
(2)关于角的分类:已知等腰三角形的
一个角是另一个角的4倍,求等腰三角形
的各内角度数。
(3)关于图形位置的分类:
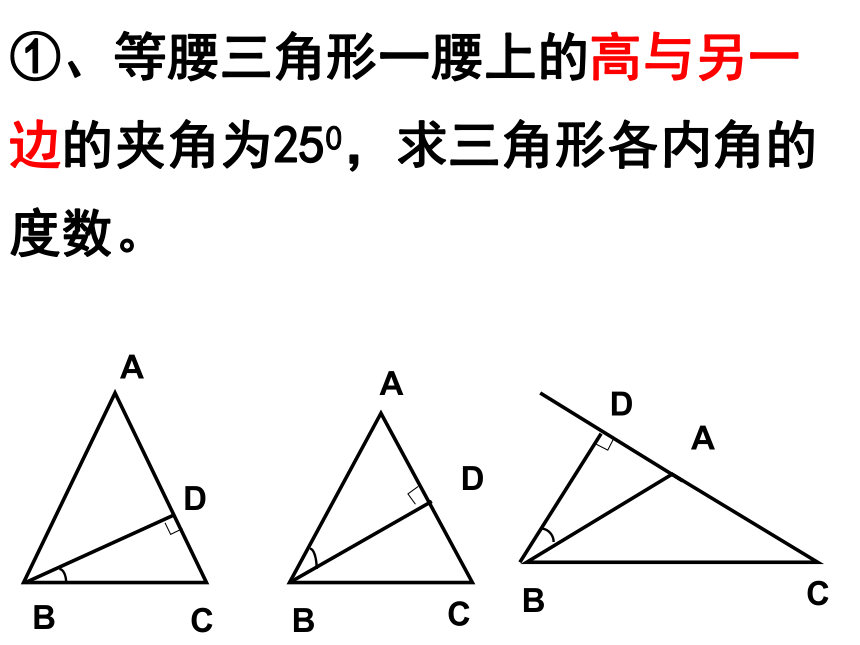
①、等腰三角形一腰上的高与另一边的夹角为250,求三角形各内角的度数。
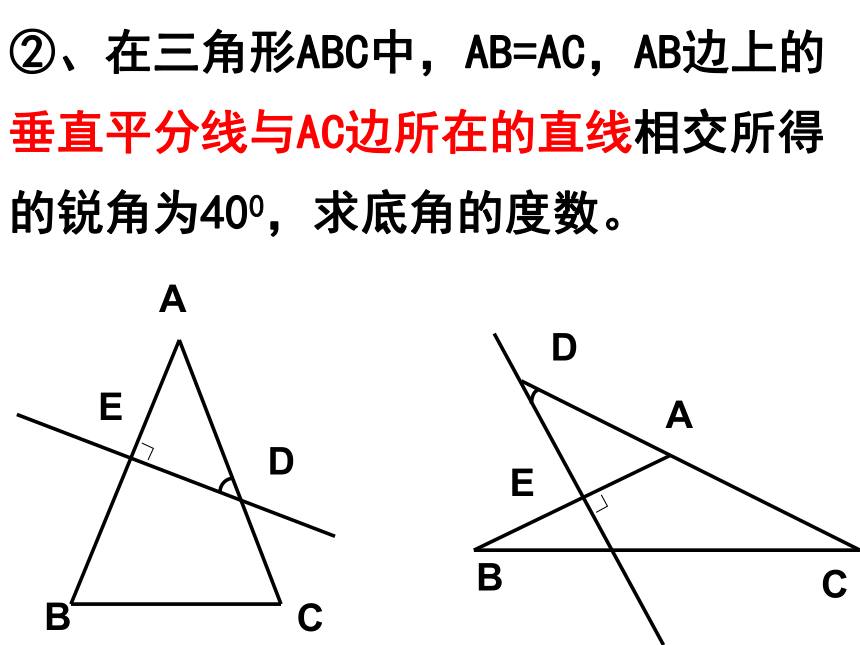
②、在三角形ABC中,AB=AC,AB边上的垂直平分线与AC边所在的直线相交所得的锐角为400,求底角的度数。
①、等腰三角形一腰上的高与另一边的夹角为250,求三角形各内角的度数。
②、在三角形ABC中,AB=AC,AB边上的垂直平分线与AC边所在的直线相交所得的锐角为400,求底角的度数。
③ 、等腰三角形的底边为5cm,一腰上的中线把其周长分为两部分的差为3cm ,求三角形的腰长。
④、在直角坐标系中,点A的坐标为(1,1),在坐标轴上找一点P,使得△OAP为等腰三角形,你可找几个点?你能写出它的坐标吗?
(1)、分类的原因:条件或结论不确定;
(2)、分类的标准:对不确定的条件或结论进行合理分类;
(3)、逐类讨论:对各类问题详细讨论,逐步解决;
(4)、检查总结:将各类情况总结归纳。
四:课时小结:
解分类讨论问题的一般步骤:
学习反思:
1、等腰三角形是一种重要的几何图形,其性质丰富多彩,相关问题也灵活多样.必须注意因条件或结论不确定而容易出现漏解的问题,上述几种分类的角度特别要引起重视.
2、在几何中有关证明和计算用方程的基本思想有时起到事半功倍的效果。
一)、 已知ΔABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求
∠BAC的度数。
∵AD ⊥BC,AD=
BC=BD=CD,
∴ ∠BAD= ∠B= ∠C=
∠CAD= 450
∴ ∠BAC= 900
∵ AD= BC= AB
AD ⊥BC
∴ ∠B= 300
∴ ∠BAC= ∠C= (1800﹣300 )= 750
∴ ∠BAC的度数为900 或750或 150
③当顶点B为直角时,高AD与腰AB重合
则有AD=AB=BC,与已知矛盾,故∠B≠ 900
二)、已知三角形ABC中,BC>AB>AC, ∠ACB=400,若D、E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数。
点D、E在点A的同侧
点D、E在点A的异侧
1、△ABC中,AB=AC,∠A=80°,则∠B= °;
2、等腰△ABC中,∠A=80°,则∠B= °;
3、有两边长分别为3cm、5cm的等腰三角形的
周长为 ;
4、等腰三角形的周长为10cm,其中一边长为2cm,
则另两边长为 ;
5、若等腰三角形腰上的高等于腰的一半,则顶角
度数为 ;
6、等腰三角形 、 、
互相重合。
二、关于分类讨论:
(1)定义:当数学问题的条件或结论不确定时就应该分类讨论。分类讨论的基本思想就是指在解决一个问题时,将问题划分成几个能用不同形式去解决的小问题,将这些小问题一一加以解决从而使问题得到解决。
(2)实质:将整体问题化为部分问题来解决。
(3)原则:分类必须不重复、不遗漏并要综合讨论结果。
你的感悟?
三、自主探究,应用分类:
(1)关于边的分类:已知实数x、y满足
+ =0,则以x、y的值为两边长的等腰三角形的周长为多少?
(2)关于角的分类:已知等腰三角形的
一个角是另一个角的4倍,求等腰三角形
的各内角度数。
(3)关于图形位置的分类:
①、等腰三角形一腰上的高与另一边的夹角为250,求三角形各内角的度数。
②、在三角形ABC中,AB=AC,AB边上的垂直平分线与AC边所在的直线相交所得的锐角为400,求底角的度数。
①、等腰三角形一腰上的高与另一边的夹角为250,求三角形各内角的度数。
②、在三角形ABC中,AB=AC,AB边上的垂直平分线与AC边所在的直线相交所得的锐角为400,求底角的度数。
③ 、等腰三角形的底边为5cm,一腰上的中线把其周长分为两部分的差为3cm ,求三角形的腰长。
④、在直角坐标系中,点A的坐标为(1,1),在坐标轴上找一点P,使得△OAP为等腰三角形,你可找几个点?你能写出它的坐标吗?
(1)、分类的原因:条件或结论不确定;
(2)、分类的标准:对不确定的条件或结论进行合理分类;
(3)、逐类讨论:对各类问题详细讨论,逐步解决;
(4)、检查总结:将各类情况总结归纳。
四:课时小结:
解分类讨论问题的一般步骤:
学习反思:
1、等腰三角形是一种重要的几何图形,其性质丰富多彩,相关问题也灵活多样.必须注意因条件或结论不确定而容易出现漏解的问题,上述几种分类的角度特别要引起重视.
2、在几何中有关证明和计算用方程的基本思想有时起到事半功倍的效果。
一)、 已知ΔABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求
∠BAC的度数。
∵AD ⊥BC,AD=
BC=BD=CD,
∴ ∠BAD= ∠B= ∠C=
∠CAD= 450
∴ ∠BAC= 900
∵ AD= BC= AB
AD ⊥BC
∴ ∠B= 300
∴ ∠BAC= ∠C= (1800﹣300 )= 750
∴ ∠BAC的度数为900 或750或 150
③当顶点B为直角时,高AD与腰AB重合
则有AD=AB=BC,与已知矛盾,故∠B≠ 900
二)、已知三角形ABC中,BC>AB>AC, ∠ACB=400,若D、E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数。
点D、E在点A的同侧
点D、E在点A的异侧
