人教版七年级上数学课件:2.1 整式单项式 (共22张PPT)
文档属性
| 名称 | 人教版七年级上数学课件:2.1 整式单项式 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 08:38:22 | ||
图片预览








文档简介
(共22张PPT)
2.1 整式
(第2课时)
义务教育教科书 数学 七年级 上册
①数与字母、字母与字母相乘省略乘号;数与数相乘用“×”号。
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤当系数为1或-1时,这个“1”省略不写.
⑥带单位时,适当加括号.
代数式的规范写法:
用含有字母的式子填空,并观察其共同特点:
1. 边长为m的正方形的周长为____,面积为___.
3. 一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
m2
4m
4. 半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
5.一台电视机原价 a 元,现按原价的9折出售,
这台电视机现在的售价是 元;
6.一个长方形的长是0.9 m,宽是a m ,这个长方
形的面积是 m2.
0.9a
0.9a
上面这些式子有什么共同特征?
自学书本P56页,回答下列问题:
1、你能给上面这些式子命名吗?
2、什么叫单项式?
3、什么叫单项式的系数?
4、什么叫单项式的次数?
5、你能说出上面这些式子的系数和次数吗?
4m
m2
2.5x
vt
2πr
πr2
0.9a
0.9a
数或字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
明晰概念
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
注意:? 是圆周率的符号,不是字母.
字母一般指的是26个英文字母
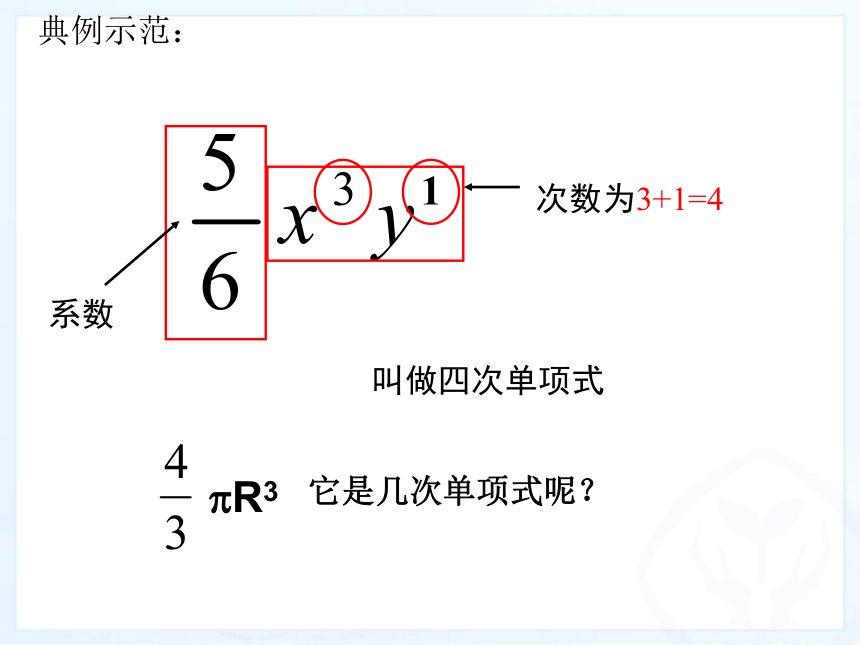
系数
1
次数为3+1=4
叫做四次单项式
?R3
它是几次单项式呢?
典例示范:
4m
m2
2.5x
vt
2πr
πr2
0.9a
0.9a
同一个式子可以表示不同的含义
1、下列各式中哪些是单项式?
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.紧扣定义:数与字母的积,可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
2、填表:
2
2
-1.2
1
1
3
-1
2
2
3
3
单项式
系数
次数
确定单项式的系数及次数时,应注意:
①系数不可漏掉π;
②系数是1或-1时,不可说没有;
③计算次数时,省略1的字母指数别漏掉;
④单项式次数只与字母指数有关;
判断下列说法是否正确:
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
以小组为单位,每个小组学生说出一个
单项式,然后请另一个小组的学生回答出所
说单项式的系数和次数,看哪一组题目出得
正确,看哪一组回答得快而准.
小组合作:写出一个含有字母X、Y单项式,并
使它的系数是-2,次数是4,那么该单项式可
以是 .
学习目标:
(1)理解单项式、单项式的系数和次数的概念.
(2)会用单项式表示简单的数量关系.
学习重点:
单项式、单项式的系数和次数的概念.
1、若X2Yn是一个四次单项式,求n
2、若X2Y|n|是一个四次单项式,求n
3、若(n-2)X2Y|n|是关于X、Y的一个四次单项式,求n
4、若X2Y|n+1|是一个四次单项式,求n
5、若单项式6X2Y4与-2Y2Zm+2的次数相同,求m的值
1.下列各式是不是单项式?为什么?
2.判断下列各说法是否正确,将错误的改正过来.
(1)单项式 的系数是0, 次数是2. ( )
(2)单项式 的系数是2, 次数是10 . ( )
(3)单项式 的系数是 ,次数是n+1 . ( )
4、若ax2yb-1是关于x,y的单项式,系数为6,次数是3,则a= ,b= .
3、若-3xa+1y是一个五次单项式,你能说出指数a是几吗?
1、单项式:
2、(1)× 系数是-1, 次数是3
(2)× 系数是27, 次数是3
(3)
√
4、a=6 b=2
5、a=-4(注意:a=2时,单项式为0)
6、m≠2 n=2
3、a=3
知识点:
单项式的概念、单项式的系数和次数的概念.
【课堂小结】
有没有困惑之处?
确定单项式的系数和次数时要注意什么?
必做作业:
教科书第57页练习第1、2题.
【布置作业】
选做作业:
1.自己写出一个单项式,并赋予它两个以上
的实际意义;
2.自己写出两个单项式,并写出它的系数和
次数.
2.1 整式
(第2课时)
义务教育教科书 数学 七年级 上册
①数与字母、字母与字母相乘省略乘号;数与数相乘用“×”号。
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤当系数为1或-1时,这个“1”省略不写.
⑥带单位时,适当加括号.
代数式的规范写法:
用含有字母的式子填空,并观察其共同特点:
1. 边长为m的正方形的周长为____,面积为___.
3. 一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
m2
4m
4. 半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
5.一台电视机原价 a 元,现按原价的9折出售,
这台电视机现在的售价是 元;
6.一个长方形的长是0.9 m,宽是a m ,这个长方
形的面积是 m2.
0.9a
0.9a
上面这些式子有什么共同特征?
自学书本P56页,回答下列问题:
1、你能给上面这些式子命名吗?
2、什么叫单项式?
3、什么叫单项式的系数?
4、什么叫单项式的次数?
5、你能说出上面这些式子的系数和次数吗?
4m
m2
2.5x
vt
2πr
πr2
0.9a
0.9a
数或字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
明晰概念
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
注意:? 是圆周率的符号,不是字母.
字母一般指的是26个英文字母
系数
1
次数为3+1=4
叫做四次单项式
?R3
它是几次单项式呢?
典例示范:
4m
m2
2.5x
vt
2πr
πr2
0.9a
0.9a
同一个式子可以表示不同的含义
1、下列各式中哪些是单项式?
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.紧扣定义:数与字母的积,可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
2、填表:
2
2
-1.2
1
1
3
-1
2
2
3
3
单项式
系数
次数
确定单项式的系数及次数时,应注意:
①系数不可漏掉π;
②系数是1或-1时,不可说没有;
③计算次数时,省略1的字母指数别漏掉;
④单项式次数只与字母指数有关;
判断下列说法是否正确:
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
以小组为单位,每个小组学生说出一个
单项式,然后请另一个小组的学生回答出所
说单项式的系数和次数,看哪一组题目出得
正确,看哪一组回答得快而准.
小组合作:写出一个含有字母X、Y单项式,并
使它的系数是-2,次数是4,那么该单项式可
以是 .
学习目标:
(1)理解单项式、单项式的系数和次数的概念.
(2)会用单项式表示简单的数量关系.
学习重点:
单项式、单项式的系数和次数的概念.
1、若X2Yn是一个四次单项式,求n
2、若X2Y|n|是一个四次单项式,求n
3、若(n-2)X2Y|n|是关于X、Y的一个四次单项式,求n
4、若X2Y|n+1|是一个四次单项式,求n
5、若单项式6X2Y4与-2Y2Zm+2的次数相同,求m的值
1.下列各式是不是单项式?为什么?
2.判断下列各说法是否正确,将错误的改正过来.
(1)单项式 的系数是0, 次数是2. ( )
(2)单项式 的系数是2, 次数是10 . ( )
(3)单项式 的系数是 ,次数是n+1 . ( )
4、若ax2yb-1是关于x,y的单项式,系数为6,次数是3,则a= ,b= .
3、若-3xa+1y是一个五次单项式,你能说出指数a是几吗?
1、单项式:
2、(1)× 系数是-1, 次数是3
(2)× 系数是27, 次数是3
(3)
√
4、a=6 b=2
5、a=-4(注意:a=2时,单项式为0)
6、m≠2 n=2
3、a=3
知识点:
单项式的概念、单项式的系数和次数的概念.
【课堂小结】
有没有困惑之处?
确定单项式的系数和次数时要注意什么?
必做作业:
教科书第57页练习第1、2题.
【布置作业】
选做作业:
1.自己写出一个单项式,并赋予它两个以上
的实际意义;
2.自己写出两个单项式,并写出它的系数和
次数.
