人教版七年级上数学课件:4.2直线射线线段第二课时 (共18张PPT)
文档属性
| 名称 | 人教版七年级上数学课件:4.2直线射线线段第二课时 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 08:40:20 | ||
图片预览





文档简介
(共18张PPT)
4.2 直线 射线 线段
第二课时
学习目标
1、会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2、培养动手操作能力,提高抽象概括能 力,能从实际问题中抽 象学问题,初步会数学的建模方法.
3、积极参与实验数学活动中,体会数学是解决实际问题的重要通过对解决问题过程的反思,懂得知识源于生活并用于生活.
(一)复习:
1、你知道线段、射线、直线的基本
概念及相互之间的区别与联系吗?
2、什么叫两点间的距离?为什么要
这样规定两点间的距离?
3、直线有什么基本性质?
目测法
(二 ) 线段的比较
第一种办法
zxxk
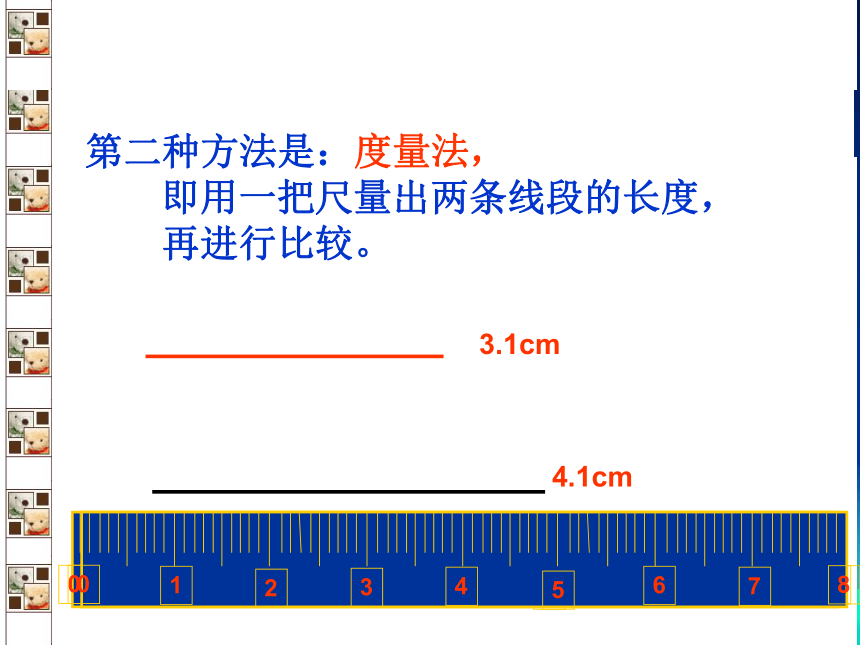
第二种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
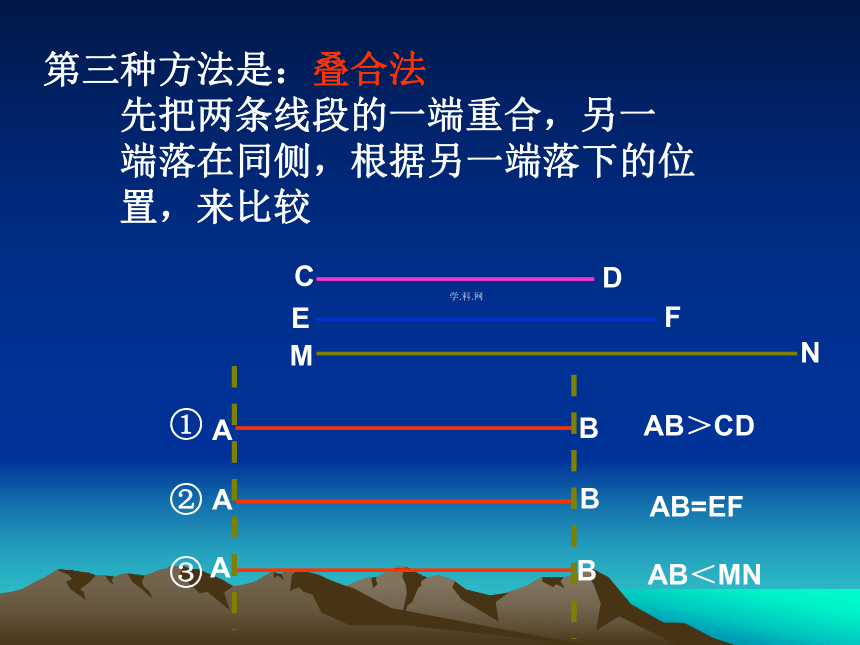
第三种方法是:叠合法
先把两条线段的一端重合,另一
端落在同侧,根据另一端落下的位
置,来比较
①
②
③
A
B
B
A
A
B
AB>CD
AB=EF
AB<MN
学.科.网
画在黑板上的两条线段是无法移动的,在没有度
量工具的情况下,请大家想想办法,如何来比较它们
的长短?
② 借助于某一物体,如铅笔、小木棒等
zxxk
小试牛刀
观察下列三组图形,分别比较线段a、b的长短。
再用刻度尺量一下,看看你的观察结果是否正确。
(1)
a
b
(2)
a
b
(3)
a
b
学科网
请先画一条线段,再画一条与它相等的线段
(不能用尺量),行吗?
你能想出几种办法?
可用圆规吗?
a
A B
D
线段的和与差
a
b
ι
ι
A B
a
C
b
AC=a+b
AD=a-b
如图(1),点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,设AB=a ,BC=b, 则线段AC就是线段a与线段b的和,记做AC = a + c ;
(1)
(2)
像这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
如图(2)线段AD就是线段a与线段b的差,记做AD =a- b.
例1 如图,已知线段a,借助圆规和直尺作一条
线段使它等于2a.
画一条线段等于已知线段a
A
C
B
a
也可以先量出线段a的长度,再画一条等于这个长度的线段。
A
线段AC=2a为所求
(三)、典型解析
例1、如图①,AD=AB- =AC+ 。
例2、如图②,下列说法不能判断点C是线段
的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB=AB
图①
图②
A B
M N
线段的中点
在一张透明的纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点就是线段的中点。动手试一试!
点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点。
A B
M
类似地,还有线段的三等分点、四等分点等。
A B
M N P
学.科.网
2、 如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.
答:AC长为3cm,AD长为1.5cm.
1、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
10
1、有A、B、C三个城市,已知A、B两城市的距离
为50千米,B、C两城市的距离为 30 千米,那么
A、C两城市的距离是( )
A、80千米 B、20千米
C、40千米 D、处于20千米到80千米间
解:如图: ∵AC=AB,
∴AB=2AC,
∴点C是AB的中点
2、“若AC=AB,则点C是线段AB的中点”这种说法
对吗?
卢小维的解答是这样的:
你认为卢小维的解答全面吗?
如果不全,漏了哪些情况?
答:不全面。漏了两种情况。
点C在AB的延长线上;或不在直线AB上。)
学科网
比较两条线段大小(长短)的方法:
目测法;
度量法;
叠合法。
基本作图:作一条线段等于已知线段。
线段的中点。
A M B
因为点M是线段AB的中点,所以 AM=BM= AB
(反过来说也是成立的。)
4.2 直线 射线 线段
第二课时
学习目标
1、会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2、培养动手操作能力,提高抽象概括能 力,能从实际问题中抽 象学问题,初步会数学的建模方法.
3、积极参与实验数学活动中,体会数学是解决实际问题的重要通过对解决问题过程的反思,懂得知识源于生活并用于生活.
(一)复习:
1、你知道线段、射线、直线的基本
概念及相互之间的区别与联系吗?
2、什么叫两点间的距离?为什么要
这样规定两点间的距离?
3、直线有什么基本性质?
目测法
(二 ) 线段的比较
第一种办法
zxxk
第二种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
第三种方法是:叠合法
先把两条线段的一端重合,另一
端落在同侧,根据另一端落下的位
置,来比较
①
②
③
A
B
B
A
A
B
AB>CD
AB=EF
AB<MN
学.科.网
画在黑板上的两条线段是无法移动的,在没有度
量工具的情况下,请大家想想办法,如何来比较它们
的长短?
② 借助于某一物体,如铅笔、小木棒等
zxxk
小试牛刀
观察下列三组图形,分别比较线段a、b的长短。
再用刻度尺量一下,看看你的观察结果是否正确。
(1)
a
b
(2)
a
b
(3)
a
b
学科网
请先画一条线段,再画一条与它相等的线段
(不能用尺量),行吗?
你能想出几种办法?
可用圆规吗?
a
A B
D
线段的和与差
a
b
ι
ι
A B
a
C
b
AC=a+b
AD=a-b
如图(1),点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,设AB=a ,BC=b, 则线段AC就是线段a与线段b的和,记做AC = a + c ;
(1)
(2)
像这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
如图(2)线段AD就是线段a与线段b的差,记做AD =a- b.
例1 如图,已知线段a,借助圆规和直尺作一条
线段使它等于2a.
画一条线段等于已知线段a
A
C
B
a
也可以先量出线段a的长度,再画一条等于这个长度的线段。
A
线段AC=2a为所求
(三)、典型解析
例1、如图①,AD=AB- =AC+ 。
例2、如图②,下列说法不能判断点C是线段
的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB=AB
图①
图②
A B
M N
线段的中点
在一张透明的纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点就是线段的中点。动手试一试!
点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点。
A B
M
类似地,还有线段的三等分点、四等分点等。
A B
M N P
学.科.网
2、 如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.
答:AC长为3cm,AD长为1.5cm.
1、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
10
1、有A、B、C三个城市,已知A、B两城市的距离
为50千米,B、C两城市的距离为 30 千米,那么
A、C两城市的距离是( )
A、80千米 B、20千米
C、40千米 D、处于20千米到80千米间
解:如图: ∵AC=AB,
∴AB=2AC,
∴点C是AB的中点
2、“若AC=AB,则点C是线段AB的中点”这种说法
对吗?
卢小维的解答是这样的:
你认为卢小维的解答全面吗?
如果不全,漏了哪些情况?
答:不全面。漏了两种情况。
点C在AB的延长线上;或不在直线AB上。)
学科网
比较两条线段大小(长短)的方法:
目测法;
度量法;
叠合法。
基本作图:作一条线段等于已知线段。
线段的中点。
A M B
因为点M是线段AB的中点,所以 AM=BM= AB
(反过来说也是成立的。)
