五年级上册数学一课一练-4.15组合图形的面积 浙教版(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-4.15组合图形的面积 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 119.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 00:00:00 | ||
图片预览


文档简介
五年级上册数学一课一练-4.15组合图形的面积
一、单选题
1.(? ???)图形与其余2个的面积不一样大。
A.?????????????????????????B.?????????????????????????C.?
2.下图中每个大三角形的大小、形状完全相同,都是正三角形,从第二排选出合适的图形,把这一个图形的序号填在(?? )里.
A.??????????????B.??????????????C.??????????????D.?
3.图中阴影部分的面积是3平方厘米.那么圆环的面积是( ??)平方厘米。
A.?9.42???????????????????????????????????B.?9???????????????????????????????????C.?18.84???????????????????????????????????D.?无法知道
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.梯形的上底下底越长,面积越大。
6.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.
三、填空题
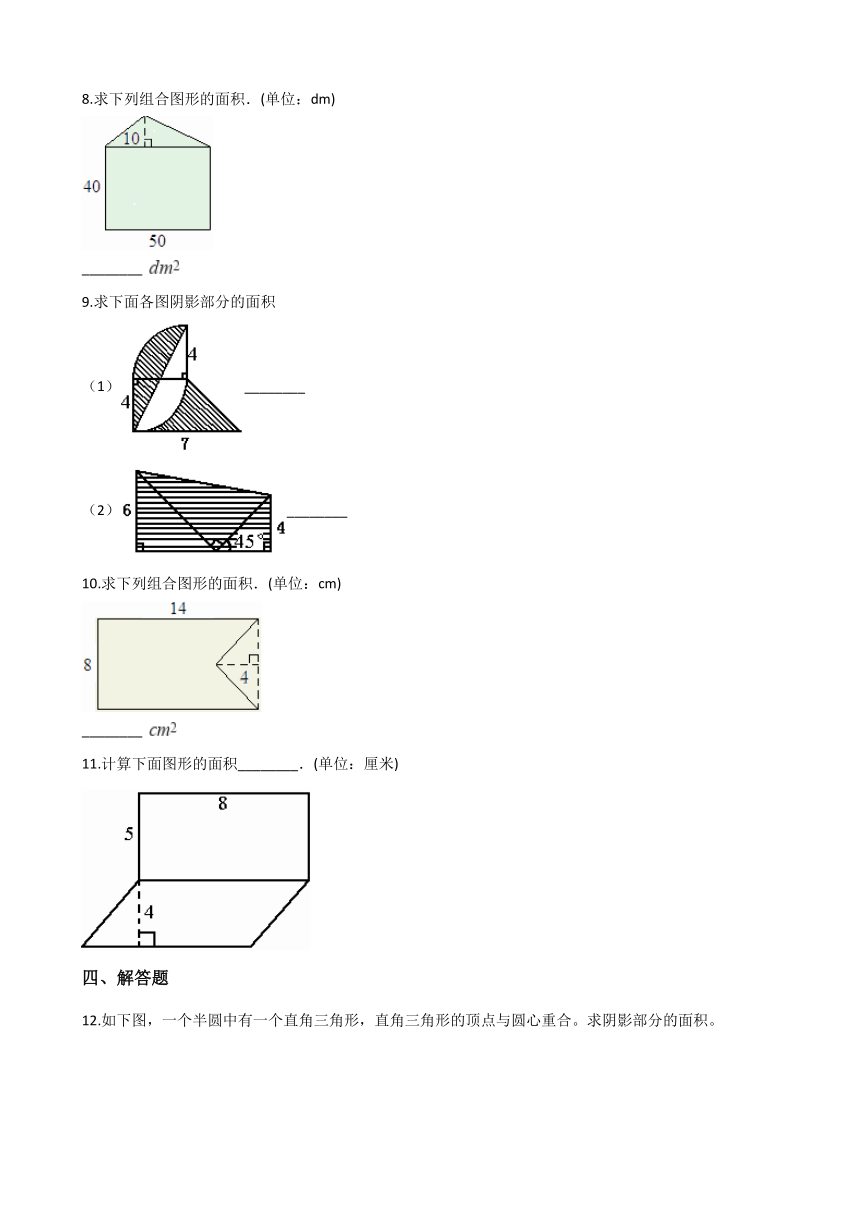
7.求下面图形的面积。(每个小方格的边长表示1cm) ?________?cm2????? ________cm2
8.求下列组合图形的面积.(单位:dm) ________
9.求下面各图阴影部分的面积
(1)________
(2)________
10.求下列组合图形的面积.(单位:cm) ________
11.计算下面图形的面积________.(单位:厘米)
四、解答题
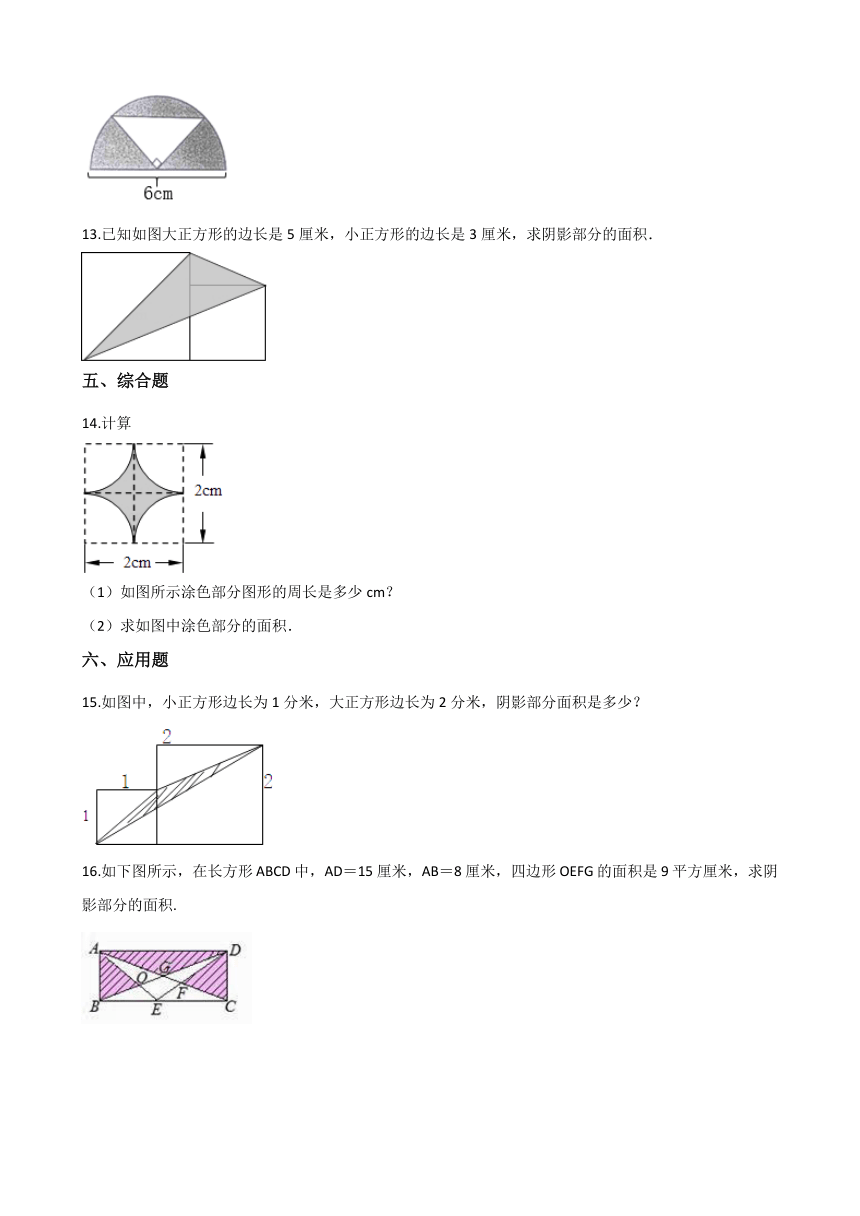
12.如下图,一个半圆中有一个直角三角形,直角三角形的顶点与圆心重合。求阴影部分的面积。
13.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积.
五、综合题
14.计算
(1)如图所示涂色部分图形的周长是多少cm?
(2)求如图中涂色部分的面积.
六、应用题
15.如图中,小正方形边长为1分米,大正方形边长为2分米,阴影部分面积是多少?
16.如下图所示,在长方形ABCD中,AD=15厘米,AB=8厘米,四边形OEFG的面积是9平方厘米,求阴影部分的面积.
参考答案
一、单选题
1.【答案】B
【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A图形的面积相等,B图形的面积与其余2个的面积不一样大. 故答案为:B.
【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.
2.【答案】 D
【解析】【解答】原题阴影部分是 故答案为:D。
【分析】根据分数的加法先求出两个三角形中阴影部分占多少,再四个选项中找到阴影部分相同的即可。
3.【答案】C
【解析】【解答】解:设外圆半径是R厘米,内圆半径是r厘米, R×R÷2-r×r÷2=3 R2-r2=6 圆环面积:S=π×(R2-r2)=3.14×6=18.84(平方厘米) 故答案为:C
【分析】外圆半径就是大三角形的直角边长,内圆半径就是小三角形的直角边长;根据阴影部分的面积是3平方厘米计算出外圆半径的平方与内圆半径的平方的差,然后根据圆环面积公式计算面积即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。 故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】错误
【解析】【解答】梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高有关系,因此梯形的上底下底越长,面积越大的说法是错误的。 故答案为:错误。 【分析】因为梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高的大小有关, 据此解答。
6.【答案】正确
【解析】【解答】解:拿走一个小方块,大正方体的表面看似少了三个面,其实又多出来三个面,所以它的表面积是不变的. 故答案为:正确. 【分析】由题意知,拼成的正方体长、宽、高应该都是2厘米,即上下各4个小方块,且每个小方块都处在一个角上,每个小方块都有三个面组成大正方体的表面,拿走一个,就少三个面,但又多了三个面,从而题目得解.此题主要考查正方体的表面积,关键是弄清楚少了三个面,又多了三个面.
三、填空题
7.【答案】16;28
【解析】【解答】(1)4×4=16(cm2); (2)3×7+2×7÷2 =21+7 =28(cm2). 故答案为:(1)16;(2)28. 【分析】(1)观察图形可知,可以将右边的凸出部分的三角形剪下,平移到左边凹进部分,刚好组成一个边长4厘米的正方形,根据正方形的面积=边长×边长,据此列式计算;(2)观察图形可知,将此图分成一个三角形和一个长方形,分别求出面积,再相加即可解答.
8.【答案】2250
【解析】【解答】40x50+50x10÷2=2250平方分米
【分析】长方形面积+三角形面积=组合图形面积
9.【答案】(1)? (2)50cm2
【解析】【解答】解:(1)4×4÷2+7×4÷2 =8+14 =22(cm2) (2)(6+4)×(6+4)÷2 =10×10÷2 =50(cm2) 故答案为:22cm2;50cm2
【分析】(1)把阴影部分重新组合后实际就是两个三角形的面积之和;(2)根据梯形面积公式计算,梯形的高是(6+4)cm.
10.【答案】96
【解析】【解答】14x8-8x4÷2=96平方厘米
【分析】大长方形面积-三角形面积=组合图形面积
11.【答案】72平方厘米
【解析】
四、解答题
12.【答案】 解:6÷2=3(cm) 3.14×32÷2-3×3÷2 =3.14×9÷2-9÷2 =14.13-4.5 =9.63(cm2) 答:阴影部分的面积是9.63cm2。
【解析】【分析】阴影部分的面积是半圆的面积减去空白部分直角三角形的面积,直角三角形的两条直角边就是圆的半径。
13.【答案】解:如图, (5-3)×5÷2+3×3÷2+3×(5-3)÷2 =2×5÷2+4.5+3×2÷2 =5+4.5+3 =12.5(平方厘米) 答:阴影部分的面积是12.5平方厘米。
【解析】【分析】可以把阴影部分分成三个三角形来计算面积,由此根据图中数据结合三角形面积公式计算即可。
五、综合题
14.【答案】 (1)解:3.14×1×2=6.28(厘米);
答:这个涂色部分的周长是6.28厘米
(2)解:2×2﹣3.14×12 ,
=4﹣3.14,
=0.86(平方厘米);
答:涂色部分的面积是0.86平方厘米
【解析】【分析】(1)根据题干可知四个角上的 圆组合在一起正好组成了一个半径为1厘米的整圆,所以涂色部分的周长就是这个半径为1厘米的圆的周长,由此利用圆的周长公式即可解决问题;(2)涂色部分的面积等于边长为2厘米的正方形的面积减去这4个 圆的面积即减去这个半径为1厘米的圆的面积,利用正方形和圆的面积公式即可解决问题.求这种不规则图形的周长和面积时,一般都要利用图形和题干中的条件,将这个问题转化到规则图形中进行解答.
六、应用题
15.【答案】解:阴影部分的面积: 1×1÷2, =1÷2, =0.5(平方分米); 答:阴影部分的面积是0.5平方分米
【解析】【分析】如图所示,连接BD,则三角形ABD与三角形DBC等底等高,所以它们的面积相等,再分别减去公共部分三角形BDE的面积,剩余部分的面积仍然相等,即三角形ABE与三角形CDE的面积相等,于是阴影部分的面积就变成了小正方形的面积的一半,小正方形的边长已知,从而可以求出阴影部分的面积.解答此题的关键是作出合适的辅助线,将阴影部分的面积转化成和小正方形的面积有关的图形的面积.
16.【答案】解:阴影部分可分为三个部分,通过面积的“等积变换”,使三部分合成一部分,使问题得到解决。三块合成一块,中间的不动,使左边的三角形右移或右边的三角形左移。
等积移动的关键是在梯形中,如下图所示图中的a,b两部分,无论它们的形状如何,都有a,b两部分的面积相等。因为三角形ABD与三角形AED的面积相等,所以三角形ABO的面积与三角形OED的面积相等。
同样的道理,三角形DFC的面积等于三角形AEF的面积。这时阴影的三部分合为一处,但四边形OEFG重复一次,即阴影部分的面积恰好等于长方形面积的一半加上四边形OEFG(9平方厘米)的面积。即阴影部分的面积是15×8÷2+9=69(平方厘米)。
【解析】
一、单选题
1.(? ???)图形与其余2个的面积不一样大。
A.?????????????????????????B.?????????????????????????C.?
2.下图中每个大三角形的大小、形状完全相同,都是正三角形,从第二排选出合适的图形,把这一个图形的序号填在(?? )里.
A.??????????????B.??????????????C.??????????????D.?
3.图中阴影部分的面积是3平方厘米.那么圆环的面积是( ??)平方厘米。
A.?9.42???????????????????????????????????B.?9???????????????????????????????????C.?18.84???????????????????????????????????D.?无法知道
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.梯形的上底下底越长,面积越大。
6.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.
三、填空题
7.求下面图形的面积。(每个小方格的边长表示1cm) ?________?cm2????? ________cm2
8.求下列组合图形的面积.(单位:dm) ________
9.求下面各图阴影部分的面积
(1)________
(2)________
10.求下列组合图形的面积.(单位:cm) ________
11.计算下面图形的面积________.(单位:厘米)
四、解答题
12.如下图,一个半圆中有一个直角三角形,直角三角形的顶点与圆心重合。求阴影部分的面积。
13.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积.
五、综合题
14.计算
(1)如图所示涂色部分图形的周长是多少cm?
(2)求如图中涂色部分的面积.
六、应用题
15.如图中,小正方形边长为1分米,大正方形边长为2分米,阴影部分面积是多少?
16.如下图所示,在长方形ABCD中,AD=15厘米,AB=8厘米,四边形OEFG的面积是9平方厘米,求阴影部分的面积.
参考答案
一、单选题
1.【答案】B
【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A图形的面积相等,B图形的面积与其余2个的面积不一样大. 故答案为:B.
【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.
2.【答案】 D
【解析】【解答】原题阴影部分是 故答案为:D。
【分析】根据分数的加法先求出两个三角形中阴影部分占多少,再四个选项中找到阴影部分相同的即可。
3.【答案】C
【解析】【解答】解:设外圆半径是R厘米,内圆半径是r厘米, R×R÷2-r×r÷2=3 R2-r2=6 圆环面积:S=π×(R2-r2)=3.14×6=18.84(平方厘米) 故答案为:C
【分析】外圆半径就是大三角形的直角边长,内圆半径就是小三角形的直角边长;根据阴影部分的面积是3平方厘米计算出外圆半径的平方与内圆半径的平方的差,然后根据圆环面积公式计算面积即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。 故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】错误
【解析】【解答】梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高有关系,因此梯形的上底下底越长,面积越大的说法是错误的。 故答案为:错误。 【分析】因为梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高的大小有关, 据此解答。
6.【答案】正确
【解析】【解答】解:拿走一个小方块,大正方体的表面看似少了三个面,其实又多出来三个面,所以它的表面积是不变的. 故答案为:正确. 【分析】由题意知,拼成的正方体长、宽、高应该都是2厘米,即上下各4个小方块,且每个小方块都处在一个角上,每个小方块都有三个面组成大正方体的表面,拿走一个,就少三个面,但又多了三个面,从而题目得解.此题主要考查正方体的表面积,关键是弄清楚少了三个面,又多了三个面.
三、填空题
7.【答案】16;28
【解析】【解答】(1)4×4=16(cm2); (2)3×7+2×7÷2 =21+7 =28(cm2). 故答案为:(1)16;(2)28. 【分析】(1)观察图形可知,可以将右边的凸出部分的三角形剪下,平移到左边凹进部分,刚好组成一个边长4厘米的正方形,根据正方形的面积=边长×边长,据此列式计算;(2)观察图形可知,将此图分成一个三角形和一个长方形,分别求出面积,再相加即可解答.
8.【答案】2250
【解析】【解答】40x50+50x10÷2=2250平方分米
【分析】长方形面积+三角形面积=组合图形面积
9.【答案】(1)? (2)50cm2
【解析】【解答】解:(1)4×4÷2+7×4÷2 =8+14 =22(cm2) (2)(6+4)×(6+4)÷2 =10×10÷2 =50(cm2) 故答案为:22cm2;50cm2
【分析】(1)把阴影部分重新组合后实际就是两个三角形的面积之和;(2)根据梯形面积公式计算,梯形的高是(6+4)cm.
10.【答案】96
【解析】【解答】14x8-8x4÷2=96平方厘米
【分析】大长方形面积-三角形面积=组合图形面积
11.【答案】72平方厘米
【解析】
四、解答题
12.【答案】 解:6÷2=3(cm) 3.14×32÷2-3×3÷2 =3.14×9÷2-9÷2 =14.13-4.5 =9.63(cm2) 答:阴影部分的面积是9.63cm2。
【解析】【分析】阴影部分的面积是半圆的面积减去空白部分直角三角形的面积,直角三角形的两条直角边就是圆的半径。
13.【答案】解:如图, (5-3)×5÷2+3×3÷2+3×(5-3)÷2 =2×5÷2+4.5+3×2÷2 =5+4.5+3 =12.5(平方厘米) 答:阴影部分的面积是12.5平方厘米。
【解析】【分析】可以把阴影部分分成三个三角形来计算面积,由此根据图中数据结合三角形面积公式计算即可。
五、综合题
14.【答案】 (1)解:3.14×1×2=6.28(厘米);
答:这个涂色部分的周长是6.28厘米
(2)解:2×2﹣3.14×12 ,
=4﹣3.14,
=0.86(平方厘米);
答:涂色部分的面积是0.86平方厘米
【解析】【分析】(1)根据题干可知四个角上的 圆组合在一起正好组成了一个半径为1厘米的整圆,所以涂色部分的周长就是这个半径为1厘米的圆的周长,由此利用圆的周长公式即可解决问题;(2)涂色部分的面积等于边长为2厘米的正方形的面积减去这4个 圆的面积即减去这个半径为1厘米的圆的面积,利用正方形和圆的面积公式即可解决问题.求这种不规则图形的周长和面积时,一般都要利用图形和题干中的条件,将这个问题转化到规则图形中进行解答.
六、应用题
15.【答案】解:阴影部分的面积: 1×1÷2, =1÷2, =0.5(平方分米); 答:阴影部分的面积是0.5平方分米
【解析】【分析】如图所示,连接BD,则三角形ABD与三角形DBC等底等高,所以它们的面积相等,再分别减去公共部分三角形BDE的面积,剩余部分的面积仍然相等,即三角形ABE与三角形CDE的面积相等,于是阴影部分的面积就变成了小正方形的面积的一半,小正方形的边长已知,从而可以求出阴影部分的面积.解答此题的关键是作出合适的辅助线,将阴影部分的面积转化成和小正方形的面积有关的图形的面积.
16.【答案】解:阴影部分可分为三个部分,通过面积的“等积变换”,使三部分合成一部分,使问题得到解决。三块合成一块,中间的不动,使左边的三角形右移或右边的三角形左移。
等积移动的关键是在梯形中,如下图所示图中的a,b两部分,无论它们的形状如何,都有a,b两部分的面积相等。因为三角形ABD与三角形AED的面积相等,所以三角形ABO的面积与三角形OED的面积相等。
同样的道理,三角形DFC的面积等于三角形AEF的面积。这时阴影的三部分合为一处,但四边形OEFG重复一次,即阴影部分的面积恰好等于长方形面积的一半加上四边形OEFG(9平方厘米)的面积。即阴影部分的面积是15×8÷2+9=69(平方厘米)。
【解析】
同课章节目录
