人教版数学四年级下册课件9 鸡兔同笼(例1)(16张PPT)
文档属性
| 名称 | 人教版数学四年级下册课件9 鸡兔同笼(例1)(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 800.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 20:34:28 | ||
图片预览






文档简介
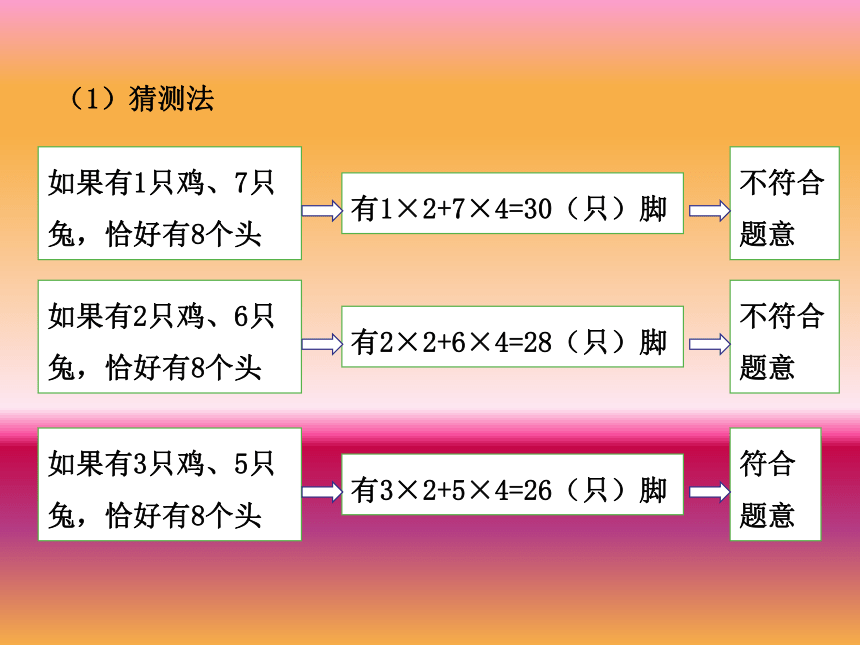
课件16张PPT。9 数学广角--鸡兔同笼一、情境引入大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。你明白上面的问题说的什么意思吗?笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?我们先从简单的问题入手。二、例题讲解笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各几只?怎么解决这个问题?(1)猜测法如果有1只鸡、7只兔,恰好有8个头有1×2+7×4=30(只)脚不符合题意如果有2只鸡、6只兔,恰好有8个头有2×2+6×4=28(只)脚不符合题意如果有3只鸡、5只兔,恰好有8个头有3×2+5×4=26(只)脚符合题意(2)列表法6220532244243526262817300832通过列表法,你发现了什么?你找到答案了吗?当3只鸡、5只兔时,脚的只数和正好是26只,所以笼子里有3只鸡、5只兔。(3)假设法如果假设笼子中全部是鸡,会出现什么结果?假设笼子里都是鸡,则脚有8×2=16(只),这样脚比原来少了26-16=10(只)。为什么会出现这样的结果呢?因为把兔看成鸡,每只兔少看了4-2=2(只)脚,也就是说兔有10÷2=5(只),这样鸡就有8-5=3(只)。怎样列式?兔的只数是(26-2×8)÷(4-2)=5(只),鸡的只数是8-5=3(只)。如果假设全部是兔,你会解答吗?假设全是兔,则脚有8×4=32(只),这样脚比实际多了
32-26=6(只),因为把一只兔看成一只鸡,就要多出4-2=2(只)脚,所以鸡一共有6÷2=3(只),这样兔就有8-3=5(只)。鸡的只数是(8×4-26)÷(4-2)=3(只),
兔的只数是8-3=5(只)。你会用假设法解答《孙子算经》中的“鸡兔同笼”问题吗?笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?假设全是鸡,则兔的只数是(94-35×2)÷(4-2)=12(只),鸡的只数是35-12=23(只)。
假设全是兔,则鸡的只数是(35×4-94)÷(4-2)=23(只),
兔的只数是35-23=12(只)。通过上面的学习,你有哪些收获?
“鸡兔同笼”问题可以用列表法进行分析,还可以用假设的方法解决。
采用“假设法”时,先假设都是同一种事物(或都是另一种事物),再根据题中给出的条件进行修正、推算。三、新知应用1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有多少只?(40×4-112)÷(4-2)
=(160-112)÷2
=48÷2
=24(只)
龟的数量:40-24=16(只)
答:龟有16只、鹤有24只。2.鸡兔同笼,头共20个,脚共62只,鸡与兔各有多少只?兔:(62-20×2)÷(4-2)=11(只)
鸡:20-11=9(只)
答:鸡有9只,兔有11只。3.在一个停车场里,现有机动车41辆,汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?汽车有(127-41×3)÷(4-3)=4(辆)
三轮摩托车有41-4=37(辆)
答:三轮摩托车有37辆。
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结1.“鸡兔同笼”问题可以用列表、假设等多种方法解答。2.假设法是假设—计算—推理—解答的过程。1. 第106页练习二十四。2. 练习册中与本课时有关系的练习题。五、课后作业
32-26=6(只),因为把一只兔看成一只鸡,就要多出4-2=2(只)脚,所以鸡一共有6÷2=3(只),这样兔就有8-3=5(只)。鸡的只数是(8×4-26)÷(4-2)=3(只),
兔的只数是8-3=5(只)。你会用假设法解答《孙子算经》中的“鸡兔同笼”问题吗?笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?假设全是鸡,则兔的只数是(94-35×2)÷(4-2)=12(只),鸡的只数是35-12=23(只)。
假设全是兔,则鸡的只数是(35×4-94)÷(4-2)=23(只),
兔的只数是35-23=12(只)。通过上面的学习,你有哪些收获?
“鸡兔同笼”问题可以用列表法进行分析,还可以用假设的方法解决。
采用“假设法”时,先假设都是同一种事物(或都是另一种事物),再根据题中给出的条件进行修正、推算。三、新知应用1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有多少只?(40×4-112)÷(4-2)
=(160-112)÷2
=48÷2
=24(只)
龟的数量:40-24=16(只)
答:龟有16只、鹤有24只。2.鸡兔同笼,头共20个,脚共62只,鸡与兔各有多少只?兔:(62-20×2)÷(4-2)=11(只)
鸡:20-11=9(只)
答:鸡有9只,兔有11只。3.在一个停车场里,现有机动车41辆,汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?汽车有(127-41×3)÷(4-3)=4(辆)
三轮摩托车有41-4=37(辆)
答:三轮摩托车有37辆。
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结1.“鸡兔同笼”问题可以用列表、假设等多种方法解答。2.假设法是假设—计算—推理—解答的过程。1. 第106页练习二十四。2. 练习册中与本课时有关系的练习题。五、课后作业
