湘教版八年级上册数学课件:4.3一元一次不等式的解法 (共15张PPT)
文档属性
| 名称 | 湘教版八年级上册数学课件:4.3一元一次不等式的解法 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 290.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
一元一次不等式的解法
复习:
1.不等式的基本性质是什么?
性质1: 不等式的两边都加上(或减去)
同一个数(或式),不等号的方向不变。
性质2: 不等式的两边都乘(或除以)
同一个正数,不等号的方向不变。
性质3:不等式的两边都乘(或除以)
同一个负数,不等号的方向改变。
解(1):
合并同类项,得 x < 6
移项,得 -5x+6x < 8-2
例1 解下列一元一次不等式 :
(1) 2-5x < 8-6x ;
(2)
解(2): 去分母,得 2(x -5)+1×6 ≤ 9x
去括号,得 2x -10 + 6 ≤ 9x
移项,得 2x - 9x ≤ 10 - 6
合并同类项,得: -7x ≤ 4
两边都除以-7,得
x ≥
求不等式的解集的过程,叫解不等式.
我们把不等式的解的全体, 叫不等式的解集.
例如 我们用x>2表示3x>6的解集.
注意:
(1)去分母时不要忘记不含分母的项(即分母的l的项)也应乘以最简公分母,还要考虑要不要加括号;
(2)乘(或除以)同一个负数时,不等号方向要改变;
(3)移项要变号;
(4)书写格式上也要注意:不等号不要连写.
2.解一元一次不等式的一般步骤是什么?
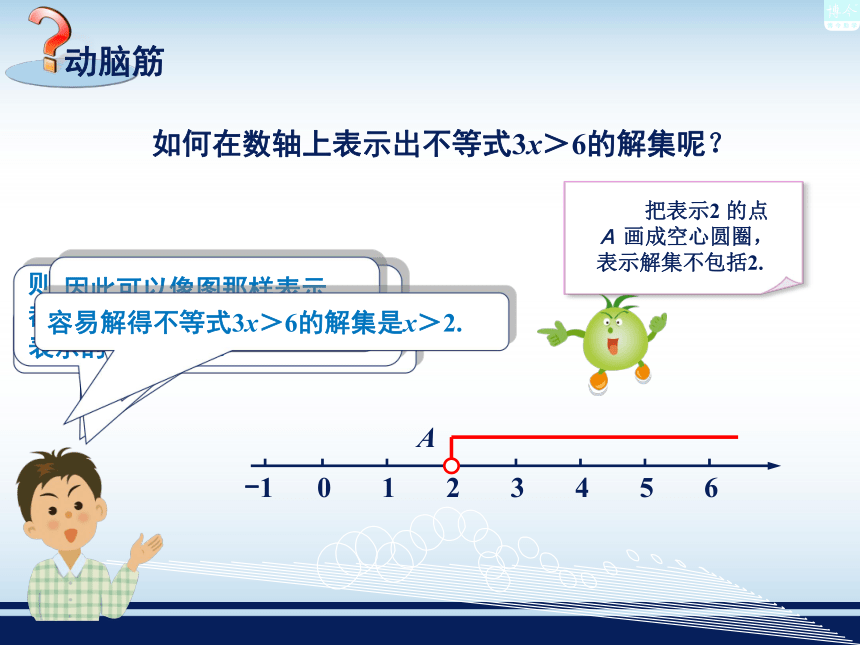
一个不等式的解集常常可以借助数轴直观地表示出来.
问?
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示3x>6的解集x>2.
动脑筋
如何在数轴上表示出不等式3x>6的解集呢?
容易解得不等式3x>6的解集是x>2.
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
在数轴上表示x ≥ -2的图是
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
(A)
(B)
(C)
(D)
(B)
小智慧 大挑战
举
例
解
解这个不等式,得 x ≤ 6
x≤6在数轴上表示如图所示:
-1
0
1
2
3
4
5
6
根据题意,得 x +2≥ 0
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例2 当x取什么值时,代数式 x+2的值大于或等于0?并求出所有满足条件的正整数.
练习
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) 4x -3<2x+3 ;
(2) .
练习
(1) x的 大于或等于2;
(2) x与2的和不小于1;
(3) y与1的差不大于0;
(4) y与5的差大于-2;
2. 先用不等式表示下列数量关系,然后求出它们的解集,并在数轴上表示出来:
中考 试题
解不等式 ,并把解集在数轴上表示出来.
-2
-1
0
1
2
3
4
去分母,得 6(2x-1)≥10x+1.
去括号,移项,合并同类项得 2x≥7.
解得
这个不等式的解集在数轴上表示如下图:
解
课堂小结:
重点学习了在数轴上表示不等式的解集
注意:
1、有没有等于这个数。(有等于画实心点“?”,没有等于就画空心圆“。”)
2、弄清方向。(“>”画右边,“<”画左边。)
作业布置:
P143
A组3、4题
谢谢大家
再见
一元一次不等式的解法
复习:
1.不等式的基本性质是什么?
性质1: 不等式的两边都加上(或减去)
同一个数(或式),不等号的方向不变。
性质2: 不等式的两边都乘(或除以)
同一个正数,不等号的方向不变。
性质3:不等式的两边都乘(或除以)
同一个负数,不等号的方向改变。
解(1):
合并同类项,得 x < 6
移项,得 -5x+6x < 8-2
例1 解下列一元一次不等式 :
(1) 2-5x < 8-6x ;
(2)
解(2): 去分母,得 2(x -5)+1×6 ≤ 9x
去括号,得 2x -10 + 6 ≤ 9x
移项,得 2x - 9x ≤ 10 - 6
合并同类项,得: -7x ≤ 4
两边都除以-7,得
x ≥
求不等式的解集的过程,叫解不等式.
我们把不等式的解的全体, 叫不等式的解集.
例如 我们用x>2表示3x>6的解集.
注意:
(1)去分母时不要忘记不含分母的项(即分母的l的项)也应乘以最简公分母,还要考虑要不要加括号;
(2)乘(或除以)同一个负数时,不等号方向要改变;
(3)移项要变号;
(4)书写格式上也要注意:不等号不要连写.
2.解一元一次不等式的一般步骤是什么?
一个不等式的解集常常可以借助数轴直观地表示出来.
问?
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示3x>6的解集x>2.
动脑筋
如何在数轴上表示出不等式3x>6的解集呢?
容易解得不等式3x>6的解集是x>2.
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
在数轴上表示x ≥ -2的图是
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
(A)
(B)
(C)
(D)
(B)
小智慧 大挑战
举
例
解
解这个不等式,得 x ≤ 6
x≤6在数轴上表示如图所示:
-1
0
1
2
3
4
5
6
根据题意,得 x +2≥ 0
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例2 当x取什么值时,代数式 x+2的值大于或等于0?并求出所有满足条件的正整数.
练习
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) 4x -3<2x+3 ;
(2) .
练习
(1) x的 大于或等于2;
(2) x与2的和不小于1;
(3) y与1的差不大于0;
(4) y与5的差大于-2;
2. 先用不等式表示下列数量关系,然后求出它们的解集,并在数轴上表示出来:
中考 试题
解不等式 ,并把解集在数轴上表示出来.
-2
-1
0
1
2
3
4
去分母,得 6(2x-1)≥10x+1.
去括号,移项,合并同类项得 2x≥7.
解得
这个不等式的解集在数轴上表示如下图:
解
课堂小结:
重点学习了在数轴上表示不等式的解集
注意:
1、有没有等于这个数。(有等于画实心点“?”,没有等于就画空心圆“。”)
2、弄清方向。(“>”画右边,“<”画左边。)
作业布置:
P143
A组3、4题
谢谢大家
再见
同课章节目录
