沪教版(五四学制)八年级数学上学期第16章 二次根式单元测试卷(解析版)
文档属性
| 名称 | 沪教版(五四学制)八年级数学上学期第16章 二次根式单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 996.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 07:25:41 | ||
图片预览
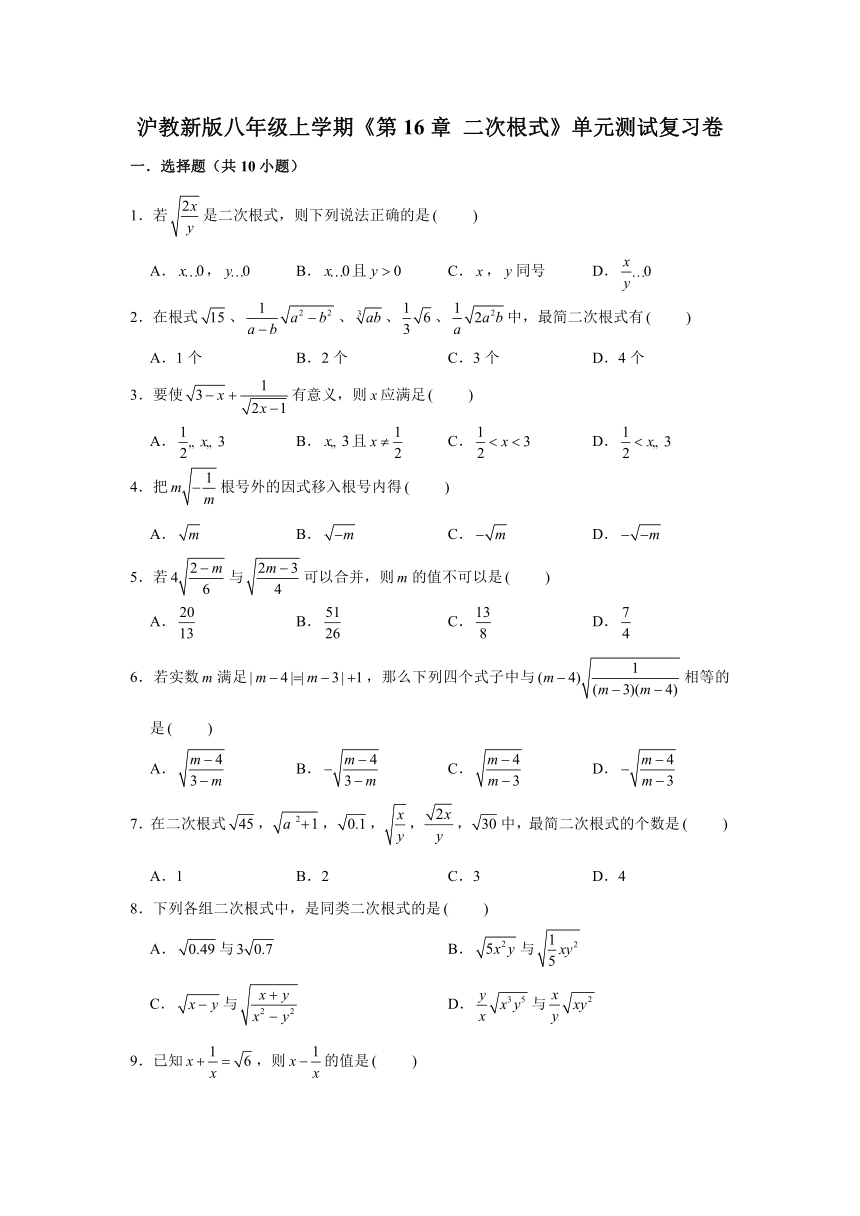




文档简介
沪教新版八年级上学期《第16章 二次根式》单元测试复习卷
一.选择题(共10小题)
1.若是二次根式,则下列说法正确的是
A., B.且 C.,同号 D.
2.在根式、、、、中,最简二次根式有
A.1个 B.2个 C.3个 D.4个
3.要使有意义,则应满足
A. B.且 C. D.
4.把根号外的因式移入根号内得
A. B. C. D.
5.若与可以合并,则的值不可以是
A. B. C. D.
6.若实数满足,那么下列四个式子中与相等的是
A. B. C. D.
7.在二次根式,,,,,中,最简二次根式的个数是
A.1 B.2 C.3 D.4
8.下列各组二次根式中,是同类二次根式的是
A.与 B.与
C.与 D.与
9.已知,则的值是
A. B. C. D.不能确定
10.已知为实数,则代数式的最小值为
A.0 B.3 C. D.9
二.填空题(共6小题)
11.计算:的结果为 .
12.若是正整数,则整数的最小值为 .
13.已知,则值为 .
14.已知最简二次根式与是同类二次根式,则的值为 .
15.观察分析,探求出规律,然后填空:,2,,,, ,, (第个数).
16.若,则 .
三.解答题(共10小题)
17.计算及解方程:
(1)
(2)
(3)
(4)
(5)解方程: (6)解方程:
18.计算:.
19.阅读下面一道题的解答过程,判断是否正确,如若不正确,请写出正确的解答过程.
化简:
解:原式.
若,.求的值.
21.若与是同类最简二次根式,则求的值.
22.当取什么值时,代数式取值最小?并求出这个最小值.
若最简二次根式与是同类二次根式,求、的值.
24.已知,求的平方根.
25.观察下列各式:;;,
请你猜想:
(1) , .
(2)计算(请写出推导过程)
(3)请你将猜想到的规律用含有自然数的代数式表达出来 .
26.我们已经知道,形如的无理数的化简要借助平方差公式:
例如:.
下面我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简?
建立模型:形如的化简,只要我们找到两个数,,使,,这样,,那么便有:,
问题解决:化简,
解:首先把化为,这里,,由于,,
即,,
模型应用
利用上述解决问题的方法化简下列各式:
(1);(2);
模型应用
(3)在中,,,,那么边的长为多少?(结果化成最简).
沪教新版八年级上学期《第16章 二次根式》单元测试复习卷
参考答案与试题解析
一.选择题(共10小题)
1.若是二次根式,则下列说法正确的是
A., B.且 C.,同号 D.
【解答】解:依题意有,即.
故选:.
2.在根式、、、、中,最简二次根式有
A.1个 B.2个 C.3个 D.4个
【解答】解:、、都是最简二次根式;
不是二次根式;,可化简;
最简二次根式有3个,故选.
3.要使有意义,则应满足
A. B.且 C. D.
【解答】解:由题意得,,
解不等式①得,,
解不等式②的,,
所以,.
故选:.
4.把根号外的因式移入根号内得
A. B. C. D.
【解答】解:成立,
,即,
原式.
故选:.
5.若与可以合并,则的值不可以是
A. B. C. D.
【解答】解:、把代入根式分别化简:,,故选项不符合题意;
、把代入根式化简:;,故选项不合题意;
、把代入根式化简:;,故选项不合题意;
、把代入根式化简:,,故符合题意.
故选:.
6.若实数满足,那么下列四个式子中与相等的是
A. B. C. D.
【解答】解:由得,,
,,
.
故选:.
7.在二次根式,,,,,中,最简二次根式的个数是
A.1 B.2 C.3 D.4
【解答】解:,,等都不是最简二次根式,
而,,是最简二次根式,
即最简二次根式有3个.
故选:.
8.下列各组二次根式中,是同类二次根式的是
A.与 B.与
C.与 D.与
【解答】解:、,不是二次根式,本项错误;
、,,不是同类二次根式,本项错误;
、与是同类二次根式,本项正确;
、,不是同类二次根式,本项错误,
故选:.
9.(易错题)已知,则的值是
A. B. C. D.不能确定
【解答】解:,
.故选.
10.已知为实数,则代数式的最小值为
A.0 B.3 C. D.9
【解答】解:原式
当,即时
代数式的值最小,为即3
故选:.
二.填空题(共6小题)
11.计算:的结果为 1 .
【解答】解:原式,
,
,
故答案为:1.
12.若是正整数,则整数的最小值为 3 .
【解答】解:是正整数,是整数,
的最小值是3.
故答案是:3.
13.已知,则值为 .
【解答】解:由题意得:得,
所以,
所以,
故答案为:.
14.已知最简二次根式与是同类二次根式,则的值为 2 .
【解答】解:依题意得:
解得:
故答案为:2
15.观察分析,探求出规律,然后填空:,2,,,, ,, (第个数).
【解答】解:,,,,
第6个数是,第个数是.
16.若,则 2018 .
【解答】解:,
,
,
由题意,得.
化简,得,
平方,得,
.
故答案为:2018
三.解答题(共10小题)
17.计算及解方程:
(1)
(2)
(3)
(4)
(5)解方程:
(6)解方程:
【解答】解:(1)
(2)
(3)
(4)
(5)解方程:
解:化简得:
,
(6)解方程:
解:化简得:
.
18.计算:.
【解答】解:原式
.
19.阅读下面一道题的解答过程,判断是否正确,如若不正确,请写出正确的解答过程.
化简:
解:原式.
【解答】解:错误,正确的是:
由二次根式的性质可知,,所以,,,
则原式.
20.若,.求的值.
【解答】解:
.
故当,时,原式.
21.若与是同类最简二次根式,则求的值.
【解答】解:由题意可知,
解得,,
即.
22.当取什么值时,代数式取值最小?并求出这个最小值.
【解答】解:,
当时,有最小值,是0.
则的最小值是1.
23.若最简二次根式与是同类二次根式,求、的值.
【解答】解:根据题意得:,
解得:.
,.
24.已知,求的平方根.
【解答】解:由题意得,且,
解得且,
所以,,
,
所以,,
所以,的平方根是.
25.观察下列各式:;;,
请你猜想:
(1) , .
(2)计算(请写出推导过程)
(3)请你将猜想到的规律用含有自然数的代数式表达出来 .
【解答】解:(1),;
(2);
(3).
26.我们已经知道,形如的无理数的化简要借助平方差公式:
例如:.
下面我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简?
建立模型:形如的化简,只要我们找到两个数,,使,,这样,,那么便有:,
问题解决:化简,
解:首先把化为,这里,,由于,,
即,,
模型应用
利用上述解决问题的方法化简下列各式:
(1);(2);
模型应用
(3)在中,,,,那么边的长为多少?(结果化成最简).
【解答】解:(1)这里,,由于,,
即,
所以;
(2)首先把化为,这里,,由于,,
即,,
所以
(3)在中,由勾股定理得,
所以,
所以,.
一.选择题(共10小题)
1.若是二次根式,则下列说法正确的是
A., B.且 C.,同号 D.
2.在根式、、、、中,最简二次根式有
A.1个 B.2个 C.3个 D.4个
3.要使有意义,则应满足
A. B.且 C. D.
4.把根号外的因式移入根号内得
A. B. C. D.
5.若与可以合并,则的值不可以是
A. B. C. D.
6.若实数满足,那么下列四个式子中与相等的是
A. B. C. D.
7.在二次根式,,,,,中,最简二次根式的个数是
A.1 B.2 C.3 D.4
8.下列各组二次根式中,是同类二次根式的是
A.与 B.与
C.与 D.与
9.已知,则的值是
A. B. C. D.不能确定
10.已知为实数,则代数式的最小值为
A.0 B.3 C. D.9
二.填空题(共6小题)
11.计算:的结果为 .
12.若是正整数,则整数的最小值为 .
13.已知,则值为 .
14.已知最简二次根式与是同类二次根式,则的值为 .
15.观察分析,探求出规律,然后填空:,2,,,, ,, (第个数).
16.若,则 .
三.解答题(共10小题)
17.计算及解方程:
(1)
(2)
(3)
(4)
(5)解方程: (6)解方程:
18.计算:.
19.阅读下面一道题的解答过程,判断是否正确,如若不正确,请写出正确的解答过程.
化简:
解:原式.
若,.求的值.
21.若与是同类最简二次根式,则求的值.
22.当取什么值时,代数式取值最小?并求出这个最小值.
若最简二次根式与是同类二次根式,求、的值.
24.已知,求的平方根.
25.观察下列各式:;;,
请你猜想:
(1) , .
(2)计算(请写出推导过程)
(3)请你将猜想到的规律用含有自然数的代数式表达出来 .
26.我们已经知道,形如的无理数的化简要借助平方差公式:
例如:.
下面我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简?
建立模型:形如的化简,只要我们找到两个数,,使,,这样,,那么便有:,
问题解决:化简,
解:首先把化为,这里,,由于,,
即,,
模型应用
利用上述解决问题的方法化简下列各式:
(1);(2);
模型应用
(3)在中,,,,那么边的长为多少?(结果化成最简).
沪教新版八年级上学期《第16章 二次根式》单元测试复习卷
参考答案与试题解析
一.选择题(共10小题)
1.若是二次根式,则下列说法正确的是
A., B.且 C.,同号 D.
【解答】解:依题意有,即.
故选:.
2.在根式、、、、中,最简二次根式有
A.1个 B.2个 C.3个 D.4个
【解答】解:、、都是最简二次根式;
不是二次根式;,可化简;
最简二次根式有3个,故选.
3.要使有意义,则应满足
A. B.且 C. D.
【解答】解:由题意得,,
解不等式①得,,
解不等式②的,,
所以,.
故选:.
4.把根号外的因式移入根号内得
A. B. C. D.
【解答】解:成立,
,即,
原式.
故选:.
5.若与可以合并,则的值不可以是
A. B. C. D.
【解答】解:、把代入根式分别化简:,,故选项不符合题意;
、把代入根式化简:;,故选项不合题意;
、把代入根式化简:;,故选项不合题意;
、把代入根式化简:,,故符合题意.
故选:.
6.若实数满足,那么下列四个式子中与相等的是
A. B. C. D.
【解答】解:由得,,
,,
.
故选:.
7.在二次根式,,,,,中,最简二次根式的个数是
A.1 B.2 C.3 D.4
【解答】解:,,等都不是最简二次根式,
而,,是最简二次根式,
即最简二次根式有3个.
故选:.
8.下列各组二次根式中,是同类二次根式的是
A.与 B.与
C.与 D.与
【解答】解:、,不是二次根式,本项错误;
、,,不是同类二次根式,本项错误;
、与是同类二次根式,本项正确;
、,不是同类二次根式,本项错误,
故选:.
9.(易错题)已知,则的值是
A. B. C. D.不能确定
【解答】解:,
.故选.
10.已知为实数,则代数式的最小值为
A.0 B.3 C. D.9
【解答】解:原式
当,即时
代数式的值最小,为即3
故选:.
二.填空题(共6小题)
11.计算:的结果为 1 .
【解答】解:原式,
,
,
故答案为:1.
12.若是正整数,则整数的最小值为 3 .
【解答】解:是正整数,是整数,
的最小值是3.
故答案是:3.
13.已知,则值为 .
【解答】解:由题意得:得,
所以,
所以,
故答案为:.
14.已知最简二次根式与是同类二次根式,则的值为 2 .
【解答】解:依题意得:
解得:
故答案为:2
15.观察分析,探求出规律,然后填空:,2,,,, ,, (第个数).
【解答】解:,,,,
第6个数是,第个数是.
16.若,则 2018 .
【解答】解:,
,
,
由题意,得.
化简,得,
平方,得,
.
故答案为:2018
三.解答题(共10小题)
17.计算及解方程:
(1)
(2)
(3)
(4)
(5)解方程:
(6)解方程:
【解答】解:(1)
(2)
(3)
(4)
(5)解方程:
解:化简得:
,
(6)解方程:
解:化简得:
.
18.计算:.
【解答】解:原式
.
19.阅读下面一道题的解答过程,判断是否正确,如若不正确,请写出正确的解答过程.
化简:
解:原式.
【解答】解:错误,正确的是:
由二次根式的性质可知,,所以,,,
则原式.
20.若,.求的值.
【解答】解:
.
故当,时,原式.
21.若与是同类最简二次根式,则求的值.
【解答】解:由题意可知,
解得,,
即.
22.当取什么值时,代数式取值最小?并求出这个最小值.
【解答】解:,
当时,有最小值,是0.
则的最小值是1.
23.若最简二次根式与是同类二次根式,求、的值.
【解答】解:根据题意得:,
解得:.
,.
24.已知,求的平方根.
【解答】解:由题意得,且,
解得且,
所以,,
,
所以,,
所以,的平方根是.
25.观察下列各式:;;,
请你猜想:
(1) , .
(2)计算(请写出推导过程)
(3)请你将猜想到的规律用含有自然数的代数式表达出来 .
【解答】解:(1),;
(2);
(3).
26.我们已经知道,形如的无理数的化简要借助平方差公式:
例如:.
下面我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简?
建立模型:形如的化简,只要我们找到两个数,,使,,这样,,那么便有:,
问题解决:化简,
解:首先把化为,这里,,由于,,
即,,
模型应用
利用上述解决问题的方法化简下列各式:
(1);(2);
模型应用
(3)在中,,,,那么边的长为多少?(结果化成最简).
【解答】解:(1)这里,,由于,,
即,
所以;
(2)首先把化为,这里,,由于,,
即,,
所以
(3)在中,由勾股定理得,
所以,
所以,.
