新疆昌吉玛纳斯县第一中学2018-2019学年高二下学期期末考试数学(文)试卷word含答案
文档属性
| 名称 | 新疆昌吉玛纳斯县第一中学2018-2019学年高二下学期期末考试数学(文)试卷word含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 21:22:04 | ||
图片预览


文档简介
数学试卷(文科)
考试时间:100分钟 分值:100分
一、选择题(每题4分,共40分)。
1.“a>0”是“|a|>0”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2 的值等于 ( )
A.1 B.-1 C.i D.-i
3.一位母亲记录了她的儿子3到9岁,数据如下表:
年龄(岁) 3 4 5 6 7 8 9
身高(cm) 94.8 104.2 108.7 117.8 124.3 130.8 139.0
请预测她儿子10岁时的身高 ( )
A.身高一定是145.83cm B.身高在145.83cm以上
C.身高在145.83cm左右 D.身高在145.83cm以下
4 已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( )
A.-=1 B.-=1 C.-=1 D.-=1
5 函数f(x)=x2-2ln x的单调递减区间是( )
A.(0,1] B.[1,+∞) C.(-∞,-1],(0,1) D.[-1,0),(0,1]
6.某西方国家流传这样的一个政治笑话:“鹅吃白菜,参议员先生也吃白菜,所以参议员先生是鹅.”结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
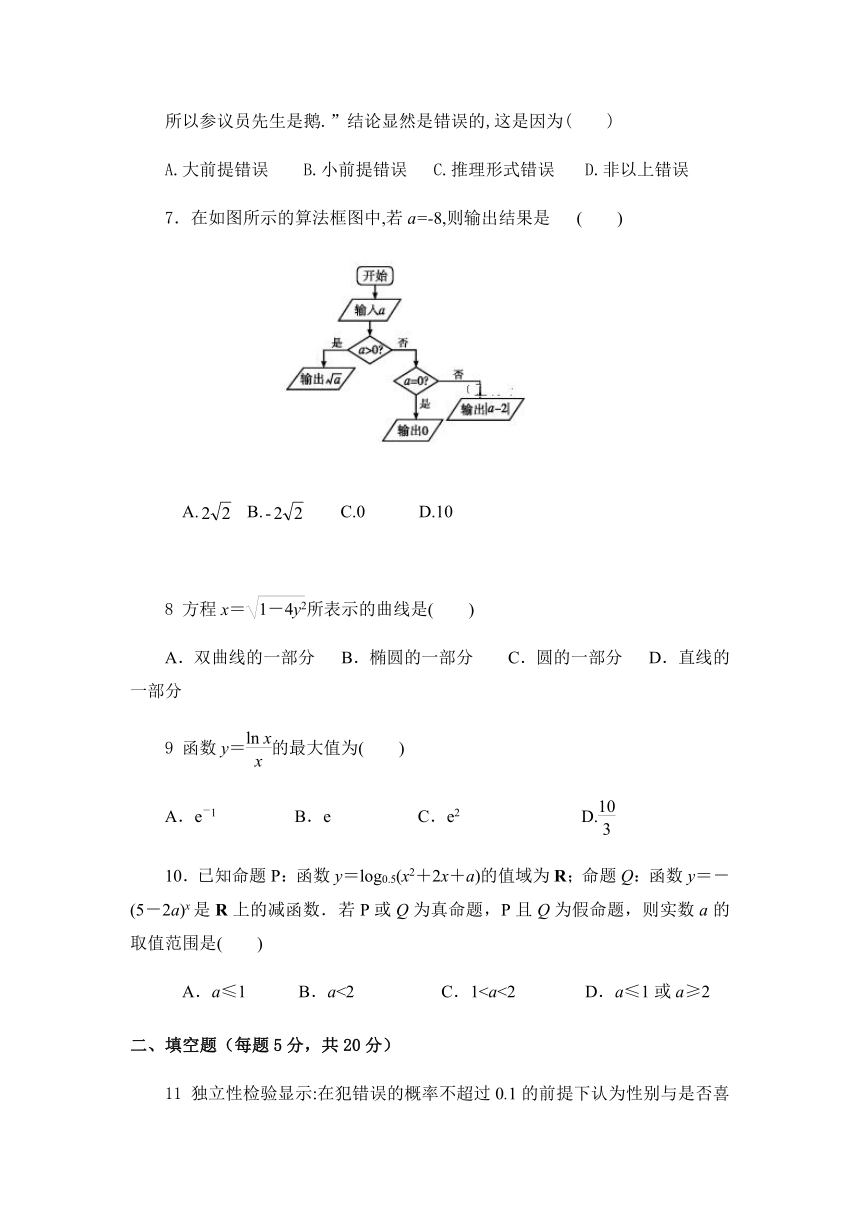
7.在如图所示的算法框图中,若a=-8,则输出结果是 ( )
A. B. C.0 D.10
8 方程x=所表示的曲线是( )
A.双曲线的一部分 B.椭圆的一部分 C.圆的一部分 D.直线的一部分
9 函数y=的最大值为( )
A.e-1 B.e C.e2 D.
10.已知命题P:函数y=log0.5(x2+2x+a)的值域为R;命题Q:函数y=-(5-2a)x是R上的减函数.若P或Q为真命题,P且Q为假命题,则实数a的取值范围是( )
A.a≤1 B.a<2 C.1
11 独立性检验显示:在犯错误的概率不超过0.1的前提下认为性别与是否喜爱喝酒有关系.则下列说法正确的是 .?
①在100名男性中约有90人爱喝酒;
②若某人爱喝酒,那么此人为男性的可能性为90%;
③认为性别与是否喜爱喝酒有关判断出错的可能性为10%;
④有90%的把握认为10名男性中有9人爱喝酒.
12.已知A,B两点的极坐标为,,则线段AB中点的直角坐标为________.
13 已知双曲线-=1 (a>0,b>0)的一条渐近线方程是y=x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为_______________________.
14 双曲线-=1 (a>0,b>0)的两个焦点F1、F2,若P为双曲线上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为________.
三、解答题:共40分 解答应写出文字说明,证明过程或演算步骤
15(10分)已知曲线C的极坐标方程是ρ=2cos θ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)当m=2时,直线l与曲线C交于A、B两点,求|AB|的值.
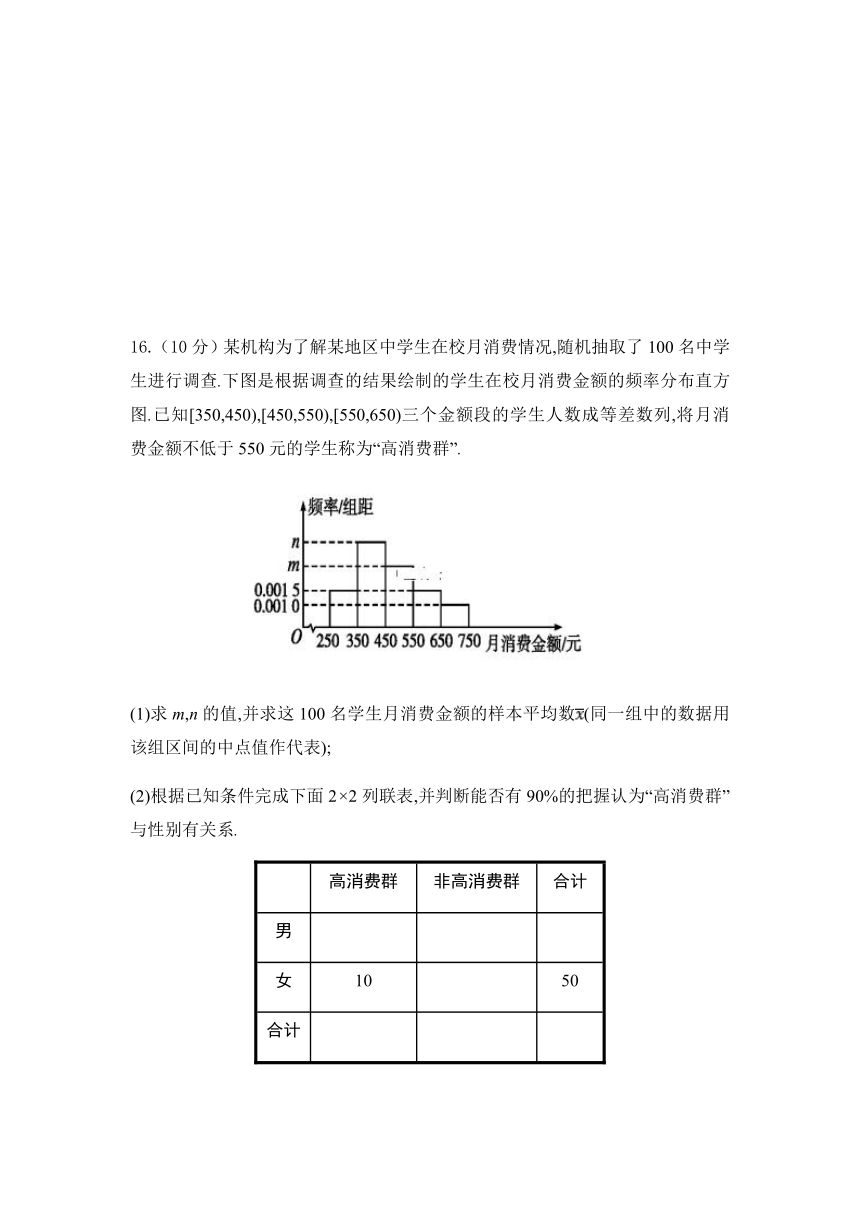
16.(10分)某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.下图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.
(1)求m,n的值,并求这100名学生月消费金额的样本平均数(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关系.
高消费群 非高消费群 合计
男
女 10 50
合计
17.(10分)已知椭圆+=1 (a>b>0)的一个顶点为A(0,1),离心率为,过点B(0,-2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2.
(1)求椭圆的方程;
(2)求△CDF2的面积
18 .(10分)已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在
点M(-1,f(-1))处的切线方程为6x-y+7=0.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
数学试卷答案
1-5 DBCAA 6-10 CDBAC
11、 ③ 12、 13、-=1 14、(1,3]
15、解:(1)由ρ=2cos θ,
得:ρ2=2ρcos θ,所以x2+y2=2x,即(x-1)2+y2=1,
所以曲线C的直角坐标方程为(x-1)2+y2=1.
由得x=y+m,
即x-y-m=0,
所以直线l的普通方程为x-y-m=0.
(2)设圆心到直线l的距离为d,
由(1)可知直线l:x-y-2=0,
曲线C:(x-1)2+y2=1,
圆C的圆心坐标为(1,0),半径1,
则圆心到直线l的距离为d==.
所以|AB|=2 =.
因此|AB|的值为.
16、解:(1)由题意知100(m+n)=0.6,且2m=n+0.001 5,
解得m=0.002 5,n=0.003 5,
所求平均数为=300×0.15+400×0.35+500×0.25+600×0.15+700×0.10=470(元).
(2)根据频率分布直方图得到如下2×2列联表:
高消费群 非高消费群 合计
男 15 35 50
女 10 40 50
合计 25 75 100
根据上表数据代入公式可得K2=≈1.33<2.706.
所以没有90%的把握认为“高消费群”与性别有关系.
17、.解 (1)由题意知b=1,e==,
又∵a2=b2+c2,∴a2=2. ∴椭圆方程为+y2=1.
(2)∵F1(-1,0),
∴直线BF1的方程为y=-2x-2,
由,得9x2+16x+6=0.
∵Δ=162-4×9×6=40>0,
∴直线与椭圆有两个公共点,
设为C(x1,y1),D(x2,y2),
则,∴|CD|=|x1-x2|=·
=·=,
又点F2到直线BF1的距离d=,故S△CDF2=|CD|·d=.
18、解 (1)由f(x)的图象经过P(0,2)知d=2,
∴f(x)=x3+bx2+cx+2,
f′(x)=3x2+2bx+c.
由在点M(-1,f(-1))处的切线方程是6x-y+7=0,知-6-f(-1)+7=0,
即f(-1)=1,f′(-1)=6.
∴即
解得b=c=-3.故所求的解析式是f(x)=x3-3x2-3x+2.
(2)f′(x)=3x2-6x-3,令3x2-6x-3=0,
即x2-2x-1=0.解得x1=1-,x2=1+.
当x<1-或x>1+时,f′(x)>0.
当1-
