北师大版数学九年级下册课件1.4解直角三角形 (共16张PPT)
文档属性
| 名称 | 北师大版数学九年级下册课件1.4解直角三角形 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
1.4 解直角三角形
第一章 直角三角形的边角关系
一个直角三角形有几个元素?它们之间有何关系?
有三条边和三个角,其中有一个角为直角
(1)三边之间的关系:
(3)边角之间的关系:锐角三角函数
(2)锐角之间的关系:∠ A+ ∠ B= 90?;
用心做一做
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 求这个三角形的其他元素.
解: 在Rt△ABC中,
例1
由直角三角形中已知的元素,
求出所有未知元素的过程,
就叫做解直角三角形
在Rt△ABC中,如果已知另一边和一个锐角,你能求出这个三角形的其他元素吗?
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 b=30,∠ B=25° ,求这个三角形的其他元素.(边长精确到1)
例2
解: 在Rt△ABC中,∠C=90°,∠ B=25°,则∠ A=65°.
在直角三角形的6个元素中直角是
已知元素,如果在知道一条边和
第三个元素,那么这个三角形所
有的元素都可以确定下来.
(1)已知a=4,b=8;
1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(角度精确到1°)
(2)已知b=10,∠B=60°;
(3)已知c=20°,∠A=60°.
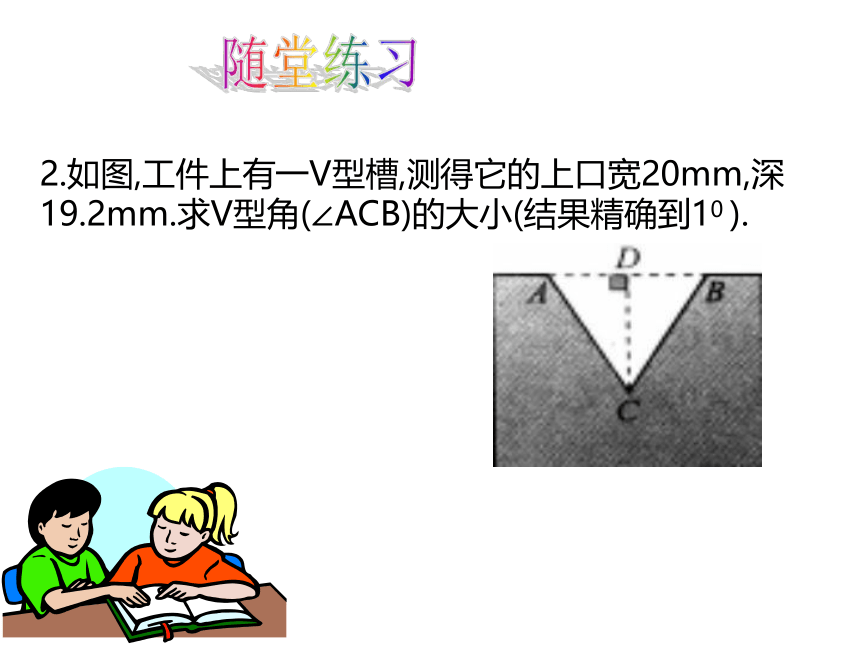
2.如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
解: ∠A=90°-∠B=90°-35°=55°
例3
例4
要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角a一般要满足50°≤∠a≤75°.如果现有一个长6m的梯子,那么
(1)使用这个梯子最高可以安全攀上多高的墙?(精确到0.1m)
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角a等于多少?(精确到1°)这时人是否能够安全使用这个梯子?
解:问题(1)可以归结为:在Rt △ABC 中,已知∠A=75°,斜边AB=6,求∠A 的对边BC 的长.
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m.
所以 BC≈6×0.97≈5.8
由计算器求得 sin75°≈0.97,
由 得
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a 的问题,可以归结为:在Rt△ABC 中,已知AC=2.4,斜边AB=6,求锐角a 的度数.
由于
利用计算器求得
a≈66°
因此当梯子底墙距离墙面2.4m时,梯子与地面
所成的角大约是66°.
由50°<66°<75°可知,这时使用这个梯子是安全的.
怎样做?
3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素.
直角三角形中的边角关系
1.填表(一式多变,适当选用):
2.模型:
已知两边求角及其三角函数 已知一边一角求另一边 已知一边一角求另一边
书本P17
习题1.5
第2题
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
想象比知识更重要.
——爱因斯坦
1.4 解直角三角形
第一章 直角三角形的边角关系
一个直角三角形有几个元素?它们之间有何关系?
有三条边和三个角,其中有一个角为直角
(1)三边之间的关系:
(3)边角之间的关系:锐角三角函数
(2)锐角之间的关系:∠ A+ ∠ B= 90?;
用心做一做
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 求这个三角形的其他元素.
解: 在Rt△ABC中,
例1
由直角三角形中已知的元素,
求出所有未知元素的过程,
就叫做解直角三角形
在Rt△ABC中,如果已知另一边和一个锐角,你能求出这个三角形的其他元素吗?
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 b=30,∠ B=25° ,求这个三角形的其他元素.(边长精确到1)
例2
解: 在Rt△ABC中,∠C=90°,∠ B=25°,则∠ A=65°.
在直角三角形的6个元素中直角是
已知元素,如果在知道一条边和
第三个元素,那么这个三角形所
有的元素都可以确定下来.
(1)已知a=4,b=8;
1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(角度精确到1°)
(2)已知b=10,∠B=60°;
(3)已知c=20°,∠A=60°.
2.如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
解: ∠A=90°-∠B=90°-35°=55°
例3
例4
要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角a一般要满足50°≤∠a≤75°.如果现有一个长6m的梯子,那么
(1)使用这个梯子最高可以安全攀上多高的墙?(精确到0.1m)
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角a等于多少?(精确到1°)这时人是否能够安全使用这个梯子?
解:问题(1)可以归结为:在Rt △ABC 中,已知∠A=75°,斜边AB=6,求∠A 的对边BC 的长.
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m.
所以 BC≈6×0.97≈5.8
由计算器求得 sin75°≈0.97,
由 得
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a 的问题,可以归结为:在Rt△ABC 中,已知AC=2.4,斜边AB=6,求锐角a 的度数.
由于
利用计算器求得
a≈66°
因此当梯子底墙距离墙面2.4m时,梯子与地面
所成的角大约是66°.
由50°<66°<75°可知,这时使用这个梯子是安全的.
怎样做?
3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素.
直角三角形中的边角关系
1.填表(一式多变,适当选用):
2.模型:
已知两边求角及其三角函数 已知一边一角求另一边 已知一边一角求另一边
书本P17
习题1.5
第2题
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
想象比知识更重要.
——爱因斯坦
