人教版九下 28.1 锐角三角函数(第一课时)说课课件(16张ppt)
文档属性
| 名称 | 人教版九下 28.1 锐角三角函数(第一课时)说课课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 276.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 14:55:31 | ||
图片预览




文档简介
课件16张PPT。§28.1锐角三角函数
(第一课时)人教版九年级数学(下册)第二十八章 内 容 导 航地位、作用;
教学目标;
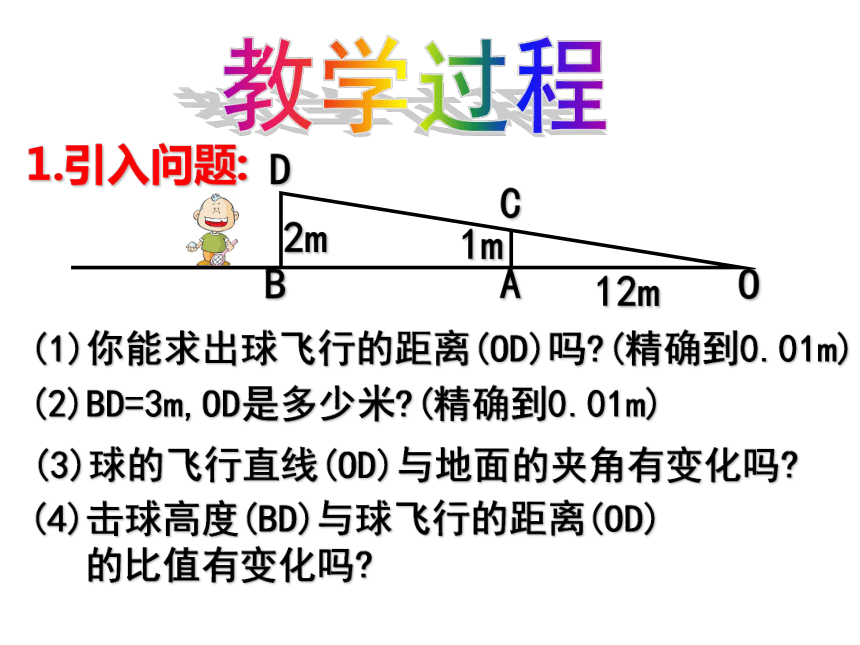
重点、难点、关键;教材分析教法设计 根据本节课的内容特点及学生的实际水平,我采用启发、观察、归纳等教学方法,注重创设问题情景,充分暴露思维过程,发展学生的思维能力。教学形式上充分利用多媒体,优化课堂教学,从生活实际出发,激发学生学习的兴趣,提高课堂效率。 学法指导 “授人以鱼,不如授人以渔”。根据本节课的特点,以实际问题为出发点,让学生自己观察、分析、归纳,让他们在活动中学会知识。教学过程1.引入问题2.探究问题3.确立课题4.研究问题5.拓展问题6.巩固训练7.反思小结8.布置作业教学过程(1)你能求出球飞行的距离(OD)吗?(精确到0.01m)(2)BD=3m,OD是多少米?(精确到0.01m)(3)球的飞行直线(OD)与地面的夹角有变化吗?(4)击球高度(BD)与球飞行的距离(OD)
的比值有变化吗?1.引入问题:教学过程2.探究问题:教学过程3.确立课题: 在Rt △ABC中,∠C=90°,把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即教学过程4.研究问题:求:(1) ∠B的对边与斜边的比值;
(2) ∠A的对边与斜边的比值;
(3) ∠D的对边与斜边的比值;
45°22教学过程5.拓展问题:拓展演示我们利用三角板验证30°、45 °、 60°
的正弦值及其变化规律,那么对于0°~ 90°
的其它锐角是否也满足这样的规律呢?教学过程6.巩固训练:如图,在Rt △ABC中,∠C=90°.
(1)若AC=4,AB=5,求sinA与sinB的值.
(2)若AC=5,AB=12,求sinA与sinB的值.
(3)若AC=n, BC=m,求sinA与sinB的值.
教学过程如图, ∠C=90°,CD⊥AB.
(1)sinB可以由哪两条线段之比? (2)若AC=5,CD=3,求sinB的值.6.巩固训练:教学过程 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足
0.77≤ sinα ≤0.97,
现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?6.巩固训练:教学过程7.反思小结:锐角三角函数----正弦教学过程8.布置作业:必做题:习题28.1第1题;
选做题:课后思考;
(第一课时)人教版九年级数学(下册)第二十八章 内 容 导 航地位、作用;
教学目标;
重点、难点、关键;教材分析教法设计 根据本节课的内容特点及学生的实际水平,我采用启发、观察、归纳等教学方法,注重创设问题情景,充分暴露思维过程,发展学生的思维能力。教学形式上充分利用多媒体,优化课堂教学,从生活实际出发,激发学生学习的兴趣,提高课堂效率。 学法指导 “授人以鱼,不如授人以渔”。根据本节课的特点,以实际问题为出发点,让学生自己观察、分析、归纳,让他们在活动中学会知识。教学过程1.引入问题2.探究问题3.确立课题4.研究问题5.拓展问题6.巩固训练7.反思小结8.布置作业教学过程(1)你能求出球飞行的距离(OD)吗?(精确到0.01m)(2)BD=3m,OD是多少米?(精确到0.01m)(3)球的飞行直线(OD)与地面的夹角有变化吗?(4)击球高度(BD)与球飞行的距离(OD)
的比值有变化吗?1.引入问题:教学过程2.探究问题:教学过程3.确立课题: 在Rt △ABC中,∠C=90°,把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即教学过程4.研究问题:求:(1) ∠B的对边与斜边的比值;
(2) ∠A的对边与斜边的比值;
(3) ∠D的对边与斜边的比值;
45°22教学过程5.拓展问题:拓展演示我们利用三角板验证30°、45 °、 60°
的正弦值及其变化规律,那么对于0°~ 90°
的其它锐角是否也满足这样的规律呢?教学过程6.巩固训练:如图,在Rt △ABC中,∠C=90°.
(1)若AC=4,AB=5,求sinA与sinB的值.
(2)若AC=5,AB=12,求sinA与sinB的值.
(3)若AC=n, BC=m,求sinA与sinB的值.
教学过程如图, ∠C=90°,CD⊥AB.
(1)sinB可以由哪两条线段之比? (2)若AC=5,CD=3,求sinB的值.6.巩固训练:教学过程 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足
0.77≤ sinα ≤0.97,
现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?6.巩固训练:教学过程7.反思小结:锐角三角函数----正弦教学过程8.布置作业:必做题:习题28.1第1题;
选做题:课后思考;
