北京课改版八年级上册12.2.1 三角形边的性质 课件(15张PPT)
文档属性
| 名称 | 北京课改版八年级上册12.2.1 三角形边的性质 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 705.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 00:00:00 | ||
图片预览





文档简介
课件15张PPT。12.2 三角形的性质
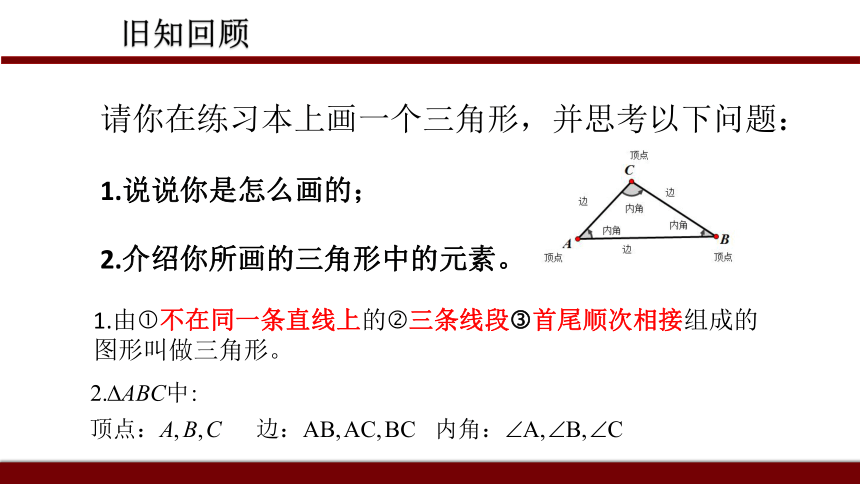
12.2.1 三角形边的性质旧知回顾请你在练习本上画一个三角形,并思考以下问题:
1.说说你是怎么画的;
2.介绍你所画的三角形中的元素。1.由?不在同一条直线上的?三条线段?首尾顺次相接组成的图形叫做三角形。一、创设情境“电动车日夜碾压,钟楼公园绿地成泥路”
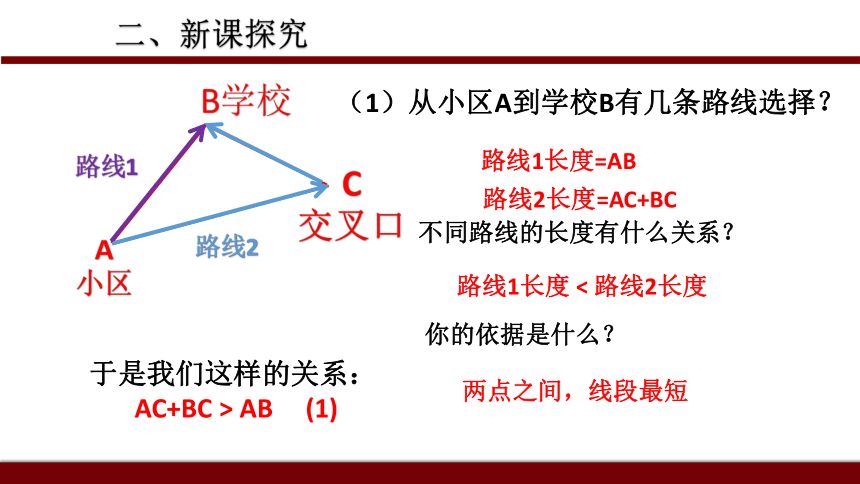
内容简述:钟楼小区和学校位于两条交叉的大路旁,经常有接送孩子的家长就在草地上碾压一条路来,请问家长们为什么要这样走呢?CBA二、新课探究A
小区B学校C
交叉口(1)从小区A到学校B有几条路线选择?路线1路线2路线1长度=AB你的依据是什么?于是我们这样的关系:
AC+BC > AB (1) 两点之间,线段最短不同路线的长度有什么关系?路线1长度 < 路线2长度路线2长度=AC+BCA
小区B学校C
交叉口(2)从A到C不同路线的长度有什么关系?请用数学式子表达出来AB+BC > AC (2)
AC+BC > AB (1)你能用一句话来概括三角形三边的关系吗?三角形两边的和大于第三边(3)从B到C不同路线的长度有什么关系?请用数学式子表达出来AB+AC > BC (3)例1:下列各组线段中,哪组可以构成三角形
?2cm,8cm,13cm
?4cm,9cm,5cm
?2cm,6cm,3cm
?3cm,4cm,5cm?注意:三角形(任意)两边之和大于第三边×××√3+4>5
3+5>44+5>3规则:一名同学说出三角形的两边后,指定另一名同学说出能与其构成三角形的第三边,其余同学给出评价。
验证的时候有没有简便的方法?较小的两边之和大于最大边,就能构成三角形。 思考与讨论:例2.如果三角形的两边长分别为4和7,那么第三边长m的取值范围是多少?三角形的第三边除了小于两边之和外,还有没有其他性质?
如何证明它呢?思考与讨论:A
BC
证明:
由已知
AB+BC > AC
AB+AC > BC
AC+BC > AB
猜想:第三边>两边之差得出:
AB > BC—AC
AC > AB—BC
BC > AC—AB
两边之差<第三边<两边之和练习
1.(口答):已知三角形两边长为3和5,则第三边c的取值范围是2?4cm,5cm,9cm
?5cm6cm,9cm例3 已知等腰三角形的周长为12cm,其中一边的长为3cm,求另外两边的长。四、拓展提高
(1)如果3cm长为底,设腰长为 xcm.
由已知条件,有
解出
(2)如果3cm长为腰,设底长为cm.
由已知条件,有
解出
因为3+3=6,不符合三角形两边之和大于第三边,所以以3cm为腰不能组成三角形。
答:另外两边的长都是4.5.解:因为长为3cm的边可能是边可能是腰,也可能是底,所以分两种情况计算。五、课堂小结1.任意三条线段都能构成三角形吗?三角形的三边具有怎样的数量关系?3.纳入系统2.你在本节课学到了哪些数学思想方法?六、布置作业必做题:《全品作业本》P58 A、B组
选做题: C组恳请各位老师批评指正
谢谢!
12.2.1 三角形边的性质旧知回顾请你在练习本上画一个三角形,并思考以下问题:
1.说说你是怎么画的;
2.介绍你所画的三角形中的元素。1.由?不在同一条直线上的?三条线段?首尾顺次相接组成的图形叫做三角形。一、创设情境“电动车日夜碾压,钟楼公园绿地成泥路”
内容简述:钟楼小区和学校位于两条交叉的大路旁,经常有接送孩子的家长就在草地上碾压一条路来,请问家长们为什么要这样走呢?CBA二、新课探究A
小区B学校C
交叉口(1)从小区A到学校B有几条路线选择?路线1路线2路线1长度=AB你的依据是什么?于是我们这样的关系:
AC+BC > AB (1) 两点之间,线段最短不同路线的长度有什么关系?路线1长度 < 路线2长度路线2长度=AC+BCA
小区B学校C
交叉口(2)从A到C不同路线的长度有什么关系?请用数学式子表达出来AB+BC > AC (2)
AC+BC > AB (1)你能用一句话来概括三角形三边的关系吗?三角形两边的和大于第三边(3)从B到C不同路线的长度有什么关系?请用数学式子表达出来AB+AC > BC (3)例1:下列各组线段中,哪组可以构成三角形
?2cm,8cm,13cm
?4cm,9cm,5cm
?2cm,6cm,3cm
?3cm,4cm,5cm?注意:三角形(任意)两边之和大于第三边×××√3+4>5
3+5>44+5>3规则:一名同学说出三角形的两边后,指定另一名同学说出能与其构成三角形的第三边,其余同学给出评价。
验证的时候有没有简便的方法?较小的两边之和大于最大边,就能构成三角形。 思考与讨论:例2.如果三角形的两边长分别为4和7,那么第三边长m的取值范围是多少?三角形的第三边除了小于两边之和外,还有没有其他性质?
如何证明它呢?思考与讨论:A
BC
证明:
由已知
AB+BC > AC
AB+AC > BC
AC+BC > AB
猜想:第三边>两边之差得出:
AB > BC—AC
AC > AB—BC
BC > AC—AB
两边之差<第三边<两边之和练习
1.(口答):已知三角形两边长为3和5,则第三边c的取值范围是2
?5cm6cm,9cm例3 已知等腰三角形的周长为12cm,其中一边的长为3cm,求另外两边的长。四、拓展提高
(1)如果3cm长为底,设腰长为 xcm.
由已知条件,有
解出
(2)如果3cm长为腰,设底长为cm.
由已知条件,有
解出
因为3+3=6,不符合三角形两边之和大于第三边,所以以3cm为腰不能组成三角形。
答:另外两边的长都是4.5.解:因为长为3cm的边可能是边可能是腰,也可能是底,所以分两种情况计算。五、课堂小结1.任意三条线段都能构成三角形吗?三角形的三边具有怎样的数量关系?3.纳入系统2.你在本节课学到了哪些数学思想方法?六、布置作业必做题:《全品作业本》P58 A、B组
选做题: C组恳请各位老师批评指正
谢谢!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
