北京课改版八年级上册11.4 无理数与实数—无理数 课件(24张PPT)
文档属性
| 名称 | 北京课改版八年级上册11.4 无理数与实数—无理数 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 15:26:18 | ||
图片预览








文档简介
课件24张PPT。课 题知识与技能:1.了解无理数的概念和它的本质特征----无限不循环;
2.会用整数估计无理数的大小; 3.知道无理数可以用数轴上的点表示;
4.会准确找出有理数及无理数。过程与方法:1.学生亲身经历无理数的发现过程,体会无理数引入的必要性,在一系列的探究活动中,让学生体验数系扩展的过程,提高学生的数学素养,形成科学的思维方式;2.培养学生的数感和估算能力;情感与态度: 1.创造一个让学生自主探索与合作交流进行学习的氛围,让学生体验探索、交流、合作的乐趣;2.在学生的讨论和问题解决的探索中,通过对学生学习方法的指导,提高学生的探究能力与合作精神;教学重点: 教学难点: 无理数概念的本质;无理数的发现过程和概念的建立 . (1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)你认为 是整数吗?是分数吗? 你能说出 它在哪两个整数之间吗?
(3)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
(4)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数? 无理数是否也可以用数轴上的点表示出来吗?
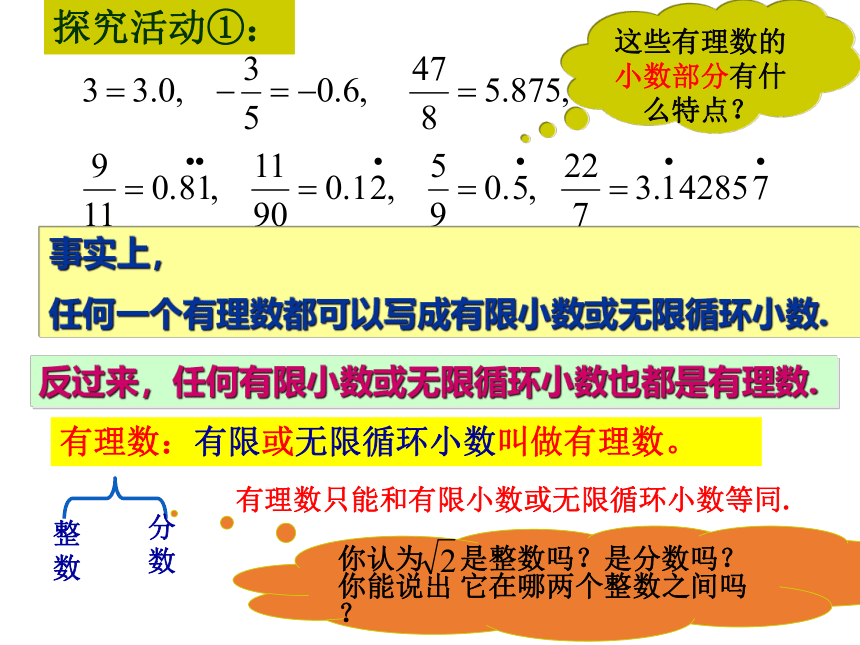
本节课将对下列问题进行探讨:想一想、做一做把下列各数表示成小数:探究活动①:(一)创设问题情景: 问题:观察它们的小数部分有什么特点?事实上,
任何一个有理数都可以写成有限小数或无限循环小数.反过来,任何有限小数或无限循环小数也都是有理数.有理数:有限或无限循环小数叫做有理数。整数分数探究活动①:这些有理数的小数部分有什么特点?有理数只能和有限小数或无限循环小数等同.(一)创设问题情景: 探究活动②:拿出边长为2cm的正方形纸片, 按照如图所示的方式折纸.问题:阴影部分的正方形的面积是多少?边长是多少?221 (二) 探索新知过程: 议一议: 我们已经知道:
是面积为2的正方形的边长;
是边长为1的正方形的对角线长;
是2的算术平方根。探究活动③ 自主探索——认识根号2的大小范围及用计算器算得的根号2的值 近似值.可见,根号2大于1.41而小于1.42.
即:自主探索——认识根号2的大小范 围及用计算器算得的根号2的值 近似值.2)一般地,分数指最简分数。两个相同的最简分数相乘,结果仍是最简分数。因此 a 不可能是分数。即根号2不是分数。取中值估值法探究活动④ 1.4142135622=_____________. 计算器显示的不是全部数据,是一个近似值.1.4142135621.999999999 再用高级电脑还能计算出更多位的数可设用计算器计算得, 所以因为1.4142135622=1.999999999<2,0 不循环的无限小数无理数的特征:注意:带根号的数不一定是无理数
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.问题1:每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?思考:如何在数轴上找到表示π的点吗?﹒O’结论:任何一个无理数均可以在数轴上准确地表示出来。探究活动⑤ 数轴上的点与有理数一一对应吗?无理数呢?11.4 无理数与实数1.无理数:无限不循环的小数叫做无理数。如:0.1010010001…〔两个1之间依次多1个0〕
2.有理数:有限小数和无限循环小数组成有理数。
3.有理数和无理数统称为实数。
4.实数的分类:实数有理数无理数正有理数零负有理数有限小数或无限循环小数正无理数负无理数无限不循环小数实数正实数负实数零正有理数正无理数正整数正分数负有理数负无理数负整数负分数实数有理数无理数整数分数正无理数负无理数正整数零负整数正分数负分数①②③例1.下列各数中,哪些是有理数?
哪些是无理数?试一试
例2 .判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并举例说明理由:(1)无理数都是开方开不尽的数 ( )
(2)无理都是无限小数. ( )
(3)无限小数都是无理数. ( )
(4)不带根号的数都是有理数. ( )
(5)带根号的数都是无理数. ( )
(6)有理数都是有限小数. ( )
(7)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合一.把下列各数分别填入相应的集合内:二、判断下列说法是否正确:1. 无理数就是客观现实不存在的数。( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
(三)归纳总结: 通过本节课的学习,你有哪些收获和体会? 1.无理数的本质特征是无限不循环; 3.数形结合的思想.作 业: 书: P48/练习1、2、
2.会用整数估计无理数的大小; 3.知道无理数可以用数轴上的点表示;
4.会准确找出有理数及无理数。过程与方法:1.学生亲身经历无理数的发现过程,体会无理数引入的必要性,在一系列的探究活动中,让学生体验数系扩展的过程,提高学生的数学素养,形成科学的思维方式;2.培养学生的数感和估算能力;情感与态度: 1.创造一个让学生自主探索与合作交流进行学习的氛围,让学生体验探索、交流、合作的乐趣;2.在学生的讨论和问题解决的探索中,通过对学生学习方法的指导,提高学生的探究能力与合作精神;教学重点: 教学难点: 无理数概念的本质;无理数的发现过程和概念的建立 . (1)观察下列有理数写成小数的形式,你有什么发现?任何有理数都能写成有限小数和无限循环小数吗?
(2)你认为 是整数吗?是分数吗? 你能说出 它在哪两个整数之间吗?
(3)请用计算器把 和 写成小数的形式,你有什么发现?像这样的数我们把它叫什么数?你还能说出一些这样的数吗?
(4)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数? 无理数是否也可以用数轴上的点表示出来吗?
本节课将对下列问题进行探讨:想一想、做一做把下列各数表示成小数:探究活动①:(一)创设问题情景: 问题:观察它们的小数部分有什么特点?事实上,
任何一个有理数都可以写成有限小数或无限循环小数.反过来,任何有限小数或无限循环小数也都是有理数.有理数:有限或无限循环小数叫做有理数。整数分数探究活动①:这些有理数的小数部分有什么特点?有理数只能和有限小数或无限循环小数等同.(一)创设问题情景: 探究活动②:拿出边长为2cm的正方形纸片, 按照如图所示的方式折纸.问题:阴影部分的正方形的面积是多少?边长是多少?221 (二) 探索新知过程: 议一议: 我们已经知道:
是面积为2的正方形的边长;
是边长为1的正方形的对角线长;
是2的算术平方根。探究活动③ 自主探索——认识根号2的大小范围及用计算器算得的根号2的值 近似值.可见,根号2大于1.41而小于1.42.
即:自主探索——认识根号2的大小范 围及用计算器算得的根号2的值 近似值.2)一般地,分数指最简分数。两个相同的最简分数相乘,结果仍是最简分数。因此 a 不可能是分数。即根号2不是分数。取中值估值法探究活动④ 1.4142135622=_____________. 计算器显示的不是全部数据,是一个近似值.1.4142135621.999999999 再用高级电脑还能计算出更多位的数可设用计算器计算得, 所以因为1.4142135622=1.999999999<2,0
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.问题1:每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?思考:如何在数轴上找到表示π的点吗?﹒O’结论:任何一个无理数均可以在数轴上准确地表示出来。探究活动⑤ 数轴上的点与有理数一一对应吗?无理数呢?11.4 无理数与实数1.无理数:无限不循环的小数叫做无理数。如:0.1010010001…〔两个1之间依次多1个0〕
2.有理数:有限小数和无限循环小数组成有理数。
3.有理数和无理数统称为实数。
4.实数的分类:实数有理数无理数正有理数零负有理数有限小数或无限循环小数正无理数负无理数无限不循环小数实数正实数负实数零正有理数正无理数正整数正分数负有理数负无理数负整数负分数实数有理数无理数整数分数正无理数负无理数正整数零负整数正分数负分数①②③例1.下列各数中,哪些是有理数?
哪些是无理数?试一试
例2 .判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并举例说明理由:(1)无理数都是开方开不尽的数 ( )
(2)无理都是无限小数. ( )
(3)无限小数都是无理数. ( )
(4)不带根号的数都是有理数. ( )
(5)带根号的数都是无理数. ( )
(6)有理数都是有限小数. ( )
(7)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合一.把下列各数分别填入相应的集合内:二、判断下列说法是否正确:1. 无理数就是客观现实不存在的数。( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
(三)归纳总结: 通过本节课的学习,你有哪些收获和体会? 1.无理数的本质特征是无限不循环; 3.数形结合的思想.作 业: 书: P48/练习1、2、
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
