人教版八年级数学下册18.1 平行四边形课件(共4课时、64张ppt)
文档属性
| 名称 | 人教版八年级数学下册18.1 平行四边形课件(共4课时、64张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 00:00:00 | ||
图片预览










文档简介
课件64张PPT。教学课件
数学 八年级下册 人教版
第十八章 平行四边形
18.1 平行四边形
第1课时生活中的平行四边学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性
质;
3.初步体会几何研究的一般思路与方法.
学习重点:
平行四边形边、角性质的证明和应用.1、如图,你能观察到图中有我们学过的
_______________________________________形. 2、举出生活中常见的平行四边形的一些其他例子,有__________________________________________ 平行四边形、长方形、三角形、梯形、正方伸缩门、竹篱笆、防护栏等 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
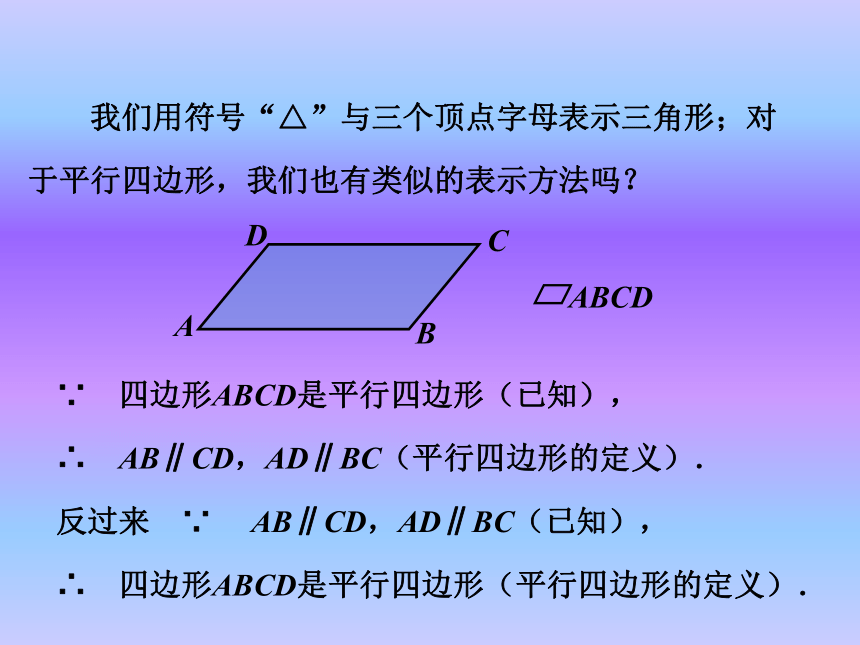
两组对边分别平行的四边形叫做平行四边形.∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义). 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? 对于平行四边形,从定义出发,你能得出它的性质吗? 你能证明这些结论吗? 给出图形定义→研究图形性质→探索图形判定条件 回忆我们的学习经历,研究几何图形的一般思路是
什么? 猜想:平行四边形对角相等,对边相等. 归纳:
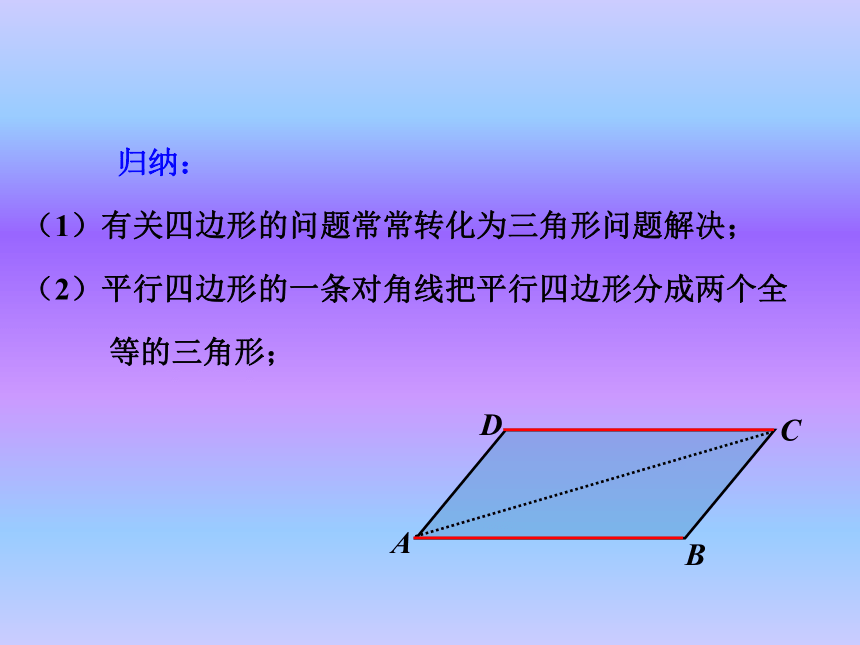
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形; 归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等. ∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD,AD=BC(平行四边形的性质),
∠DAB=∠DCB,∠B=∠D(平行四边形的性质). 问题1 如图,在平行四边形ABCD中,∠B=40°,求其余三个角的度数.几何语言:定理1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=BC(平行四边形的对边相等) .∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) .∠A= ∠C, ∠B= ∠D(平行四边形的对角相等). 定理2:平行四边形的两组对角分别相等解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8 m,
∴CD=8 m.
又AB+BC+CD+AD=36,
∴ AD=BC=10 m.8 m如图,小明用一根36 m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8 m,其他三条边各长多少? DE=BF 吗? 例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么? 平行线间的距离 例3 △ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你认
为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?你
认为有必要进一步研究思考吗?第十八章 平行四边形
18.1 平行四边形
第2课时1.两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD是平行四边形记作: ABCD平行四边形的相关概念2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.3.平行四边形相对的边称为 对边, 相对的角称为对角.对边:AB与CD, BC与DA.对角: ∠ABC与∠CDA, ∠BAD与∠DCB.学习目标:
1.掌握平行四边形对角线互相平分的性质;
2.经历对平行四边形性质的猜想与证明的过程,渗
透转化思想,体会图形性质探究的一般思路.
学习重点:
平行四边形对角线性质的探究与应用. 平行四边形的性质:
AD∥BC,AB∥CD;
AB=CD,AD=BC;
∠A=∠C,∠B=∠D. 把平行四边形问题转化为三角形问题. 一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的: 如何判断如图的四个三角形
面积相等? 问题1 想一想,平行四边形除了边、角这两个要素
的性质外,对角线有什么性质? 如图,在 ABCD中,连接AC,BD,并设它们交
于点O,OA与OC,OB与OD有什么关系? 猜想:平行四边形的
对角线互相平分. 问题2 你能证明上述猜想吗? 如图,在 ABCD中,对角线AC,BD 相交于点O.
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD. 证明:∵ 四边形
ABCD是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠1=∠2,∠3=∠4,
∴ △COD≌△AOB,
∴ OA=OC,OB=OD. 定理:平行四边形的对角线互相平分.
我们证明了平行四边形具有以下性质:
(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
前面问题中,老人分的土地面积相等吗? O●MA B C D O E F 图中还有哪些量相等? 变式 在上题中,EF过点O,且与AB,CD分别相
交于点E,F.求证:OE=OF.O EF(2) 在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。●●●●练习 如图, ABCD的对角线AC,BD相交于点O.已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为___________.2cm或8cm平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的对角线互相平分.(1)本节学习了平行四边形的哪些性质?
(2)结合本节的学习,谈谈研究平行四边形性质的思
想方法.研究平行四边形,常常把它转化为三角形问题.第十八章 平行四边形
18.1 平行四边形
第3课时有两组对边分别平行的四边形叫做平行四边形.平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分学习目标:
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条
件灵活选取适当的判定定理进行推理.
学习重点:
平行四边形三个判定定理的探究与应用.有一块平行四边形的玻璃块,假如不小
心碰碎了一部分,聪明的技师拿着细绳
很快将原来的平行四边形画了出来,你
知道他用的是什么方法吗?
答:他是根据平行四边形的定义:
两组对边分别的四边形是平行四边形。 平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.判定性质定义判定性质定义 问题 如何寻找平行四边形的判定方法? 当我们对前进的方向感到迷茫时,不妨回过头来看
看走过的路!直角三角
形的性质 直角三角
形的判定 勾股定理 勾股定理
的逆定理 在过去的学习中,类似的情况还有吗?请举例说明.
这些经验可以给我们怎样的启示?两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
边形是平行四边形 思考:这些猜想正确吗? 证明:如图,连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 两组对边分别相等的四边形是平行四边形. 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 两组对角分别相等的四边形是平行四边形.判定定理2 猜想2 如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 判定定理3 猜想3 证明:∵OA=OC,OB=OD,∠AOD=∠COB,
∴△AOD≌△COB.
∴∠OAD=∠OCB.
∴AD∥BC.
同理AB∥DC.
∴四边形ABCD是平行四边形. 证明:∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DC=EF,DE=CF,
∴四边形DCFE也是平行四边形.
∴DC∥EF.
∴AB∥EF. 例1 如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF. 现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形. 这张图揭示了定义、性质、判定间的逻辑关系,提
供了研究几何图形的一般思路. 在研究平行四边形判定的过程中,我们经历了两个
阶段,哪两个阶段呢?第十八章 平行四边形
18.1 平行四边形
第4课时 两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行平行四边形的判定方法共有几种?一组对边平行且相等四边形是平行四边形边角对角线例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力. ?
学习重点:
探索并证明三角形中位线定理.定义:把连接三角形两边中点的线段叫做三角形的中位线. 如图,在△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线. 看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系? 我们在研究平行四边形时,经常采用把平行四边形
问题转化为三角形问题,能否用平行四边形研究三角形
呢? 你能对照图形写出已知、求证吗?
怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,说
出辅助线的画法;如不可行,请说明原因. 请用适当的方法证明猜想.
请用自己的语言说出得到的结论,并比较证明方法
的异同. 三角形的中位线定理:三角形的中位线平行于三角
形的第三边,并且等于第三边的一半. 如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.18DE,DFCF 5①有一组对边平行的四边形是平行四边形。②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题1.如图,点D、E、分别为△ABC的边AB、AC的中点.求证:DE∥BC且DE= BC.2.如图,在△ABC中,D、E、F分别是
AB、BC、CA的中点.以这些点为顶点,
在图中,你能画出多少个平行四边形?为
什么?DFE答:3个例1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?例2.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC1、如下图,在△ABC中,D、E分别是AB、AC的中点,BC=10 cm,则DE= .5 cm2、如上图, 在△ABC中,D、E分别是AB、
AC的中点,∠A=50°, ∠B=70°,则∠AED= 。60° (1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会? 三角形中位线定理:
连接三角形两边中点的线段平行于第三边,且等于
第三边的一半. 我们既可以用三角形知识研究平行四边形的问题,
又可以用平行四边形知识研究三角形的问题.
数学 八年级下册 人教版
第十八章 平行四边形
18.1 平行四边形
第1课时生活中的平行四边学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性
质;
3.初步体会几何研究的一般思路与方法.
学习重点:
平行四边形边、角性质的证明和应用.1、如图,你能观察到图中有我们学过的
_______________________________________形. 2、举出生活中常见的平行四边形的一些其他例子,有__________________________________________ 平行四边形、长方形、三角形、梯形、正方伸缩门、竹篱笆、防护栏等 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义). 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? 对于平行四边形,从定义出发,你能得出它的性质吗? 你能证明这些结论吗? 给出图形定义→研究图形性质→探索图形判定条件 回忆我们的学习经历,研究几何图形的一般思路是
什么? 猜想:平行四边形对角相等,对边相等. 归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形; 归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等. ∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD,AD=BC(平行四边形的性质),
∠DAB=∠DCB,∠B=∠D(平行四边形的性质). 问题1 如图,在平行四边形ABCD中,∠B=40°,求其余三个角的度数.几何语言:定理1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=BC(平行四边形的对边相等) .∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) .∠A= ∠C, ∠B= ∠D(平行四边形的对角相等). 定理2:平行四边形的两组对角分别相等解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8 m,
∴CD=8 m.
又AB+BC+CD+AD=36,
∴ AD=BC=10 m.8 m如图,小明用一根36 m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8 m,其他三条边各长多少? DE=BF 吗? 例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么? 平行线间的距离 例3 △ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你认
为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?你
认为有必要进一步研究思考吗?第十八章 平行四边形
18.1 平行四边形
第2课时1.两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD是平行四边形记作: ABCD平行四边形的相关概念2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.3.平行四边形相对的边称为 对边, 相对的角称为对角.对边:AB与CD, BC与DA.对角: ∠ABC与∠CDA, ∠BAD与∠DCB.学习目标:
1.掌握平行四边形对角线互相平分的性质;
2.经历对平行四边形性质的猜想与证明的过程,渗
透转化思想,体会图形性质探究的一般思路.
学习重点:
平行四边形对角线性质的探究与应用. 平行四边形的性质:
AD∥BC,AB∥CD;
AB=CD,AD=BC;
∠A=∠C,∠B=∠D. 把平行四边形问题转化为三角形问题. 一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的: 如何判断如图的四个三角形
面积相等? 问题1 想一想,平行四边形除了边、角这两个要素
的性质外,对角线有什么性质? 如图,在 ABCD中,连接AC,BD,并设它们交
于点O,OA与OC,OB与OD有什么关系? 猜想:平行四边形的
对角线互相平分. 问题2 你能证明上述猜想吗? 如图,在 ABCD中,对角线AC,BD 相交于点O.
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD. 证明:∵ 四边形
ABCD是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠1=∠2,∠3=∠4,
∴ △COD≌△AOB,
∴ OA=OC,OB=OD. 定理:平行四边形的对角线互相平分.
我们证明了平行四边形具有以下性质:
(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
前面问题中,老人分的土地面积相等吗? O●MA B C D O E F 图中还有哪些量相等? 变式 在上题中,EF过点O,且与AB,CD分别相
交于点E,F.求证:OE=OF.O EF(2) 在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。●●●●练习 如图, ABCD的对角线AC,BD相交于点O.已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为___________.2cm或8cm平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的对角线互相平分.(1)本节学习了平行四边形的哪些性质?
(2)结合本节的学习,谈谈研究平行四边形性质的思
想方法.研究平行四边形,常常把它转化为三角形问题.第十八章 平行四边形
18.1 平行四边形
第3课时有两组对边分别平行的四边形叫做平行四边形.平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分学习目标:
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条
件灵活选取适当的判定定理进行推理.
学习重点:
平行四边形三个判定定理的探究与应用.有一块平行四边形的玻璃块,假如不小
心碰碎了一部分,聪明的技师拿着细绳
很快将原来的平行四边形画了出来,你
知道他用的是什么方法吗?
答:他是根据平行四边形的定义:
两组对边分别的四边形是平行四边形。 平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.判定性质定义判定性质定义 问题 如何寻找平行四边形的判定方法? 当我们对前进的方向感到迷茫时,不妨回过头来看
看走过的路!直角三角
形的性质 直角三角
形的判定 勾股定理 勾股定理
的逆定理 在过去的学习中,类似的情况还有吗?请举例说明.
这些经验可以给我们怎样的启示?两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
边形是平行四边形 思考:这些猜想正确吗? 证明:如图,连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 两组对边分别相等的四边形是平行四边形. 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 两组对角分别相等的四边形是平行四边形.判定定理2 猜想2 如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 判定定理3 猜想3 证明:∵OA=OC,OB=OD,∠AOD=∠COB,
∴△AOD≌△COB.
∴∠OAD=∠OCB.
∴AD∥BC.
同理AB∥DC.
∴四边形ABCD是平行四边形. 证明:∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DC=EF,DE=CF,
∴四边形DCFE也是平行四边形.
∴DC∥EF.
∴AB∥EF. 例1 如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF. 现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形. 这张图揭示了定义、性质、判定间的逻辑关系,提
供了研究几何图形的一般思路. 在研究平行四边形判定的过程中,我们经历了两个
阶段,哪两个阶段呢?第十八章 平行四边形
18.1 平行四边形
第4课时 两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行平行四边形的判定方法共有几种?一组对边平行且相等四边形是平行四边形边角对角线例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力. ?
学习重点:
探索并证明三角形中位线定理.定义:把连接三角形两边中点的线段叫做三角形的中位线. 如图,在△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线. 看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系? 我们在研究平行四边形时,经常采用把平行四边形
问题转化为三角形问题,能否用平行四边形研究三角形
呢? 你能对照图形写出已知、求证吗?
怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,说
出辅助线的画法;如不可行,请说明原因. 请用适当的方法证明猜想.
请用自己的语言说出得到的结论,并比较证明方法
的异同. 三角形的中位线定理:三角形的中位线平行于三角
形的第三边,并且等于第三边的一半. 如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.18DE,DFCF 5①有一组对边平行的四边形是平行四边形。②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题1.如图,点D、E、分别为△ABC的边AB、AC的中点.求证:DE∥BC且DE= BC.2.如图,在△ABC中,D、E、F分别是
AB、BC、CA的中点.以这些点为顶点,
在图中,你能画出多少个平行四边形?为
什么?DFE答:3个例1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?例2.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC1、如下图,在△ABC中,D、E分别是AB、AC的中点,BC=10 cm,则DE= .5 cm2、如上图, 在△ABC中,D、E分别是AB、
AC的中点,∠A=50°, ∠B=70°,则∠AED= 。60° (1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会? 三角形中位线定理:
连接三角形两边中点的线段平行于第三边,且等于
第三边的一半. 我们既可以用三角形知识研究平行四边形的问题,
又可以用平行四边形知识研究三角形的问题.
