人教版八年级数学下册18.2.1 矩形课件(共2课时、31张ppt)
文档属性
| 名称 | 人教版八年级数学下册18.2.1 矩形课件(共2课时、31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 596.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 00:00:00 | ||
图片预览




文档简介
课件31张PPT。教学课件
数学 八年级下册 人教版
第十八章 平行四边形
18.2.1 矩形
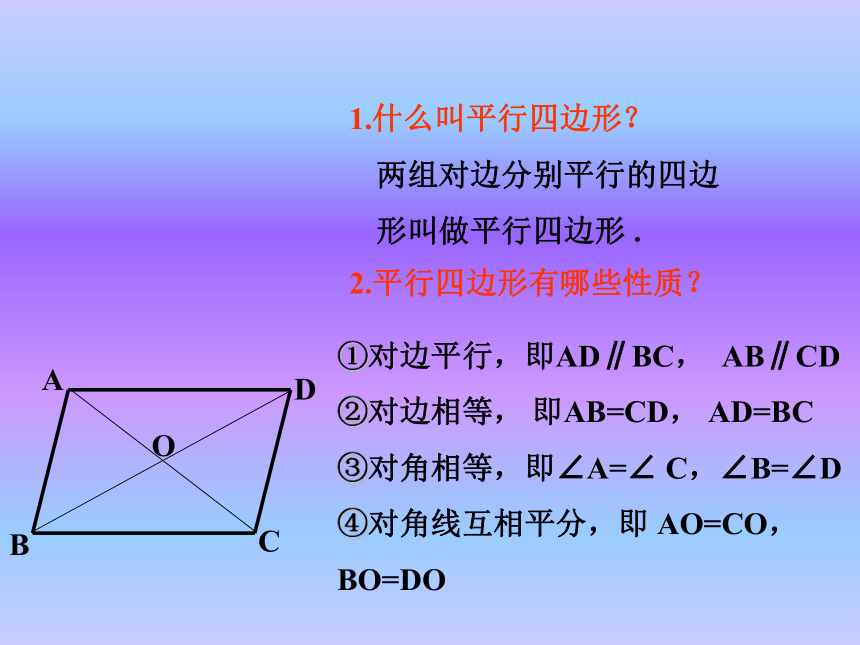
第1课时1.什么叫平行四边形?2.平行四边形有哪些性质?两组对边分别平行的四边形叫做平行四边形 .O①对边平行,即AD∥BC, AB∥CD
②对边相等, 即AB=CD, AD=BC
③对角相等,即∠A=∠ C,∠B=∠D
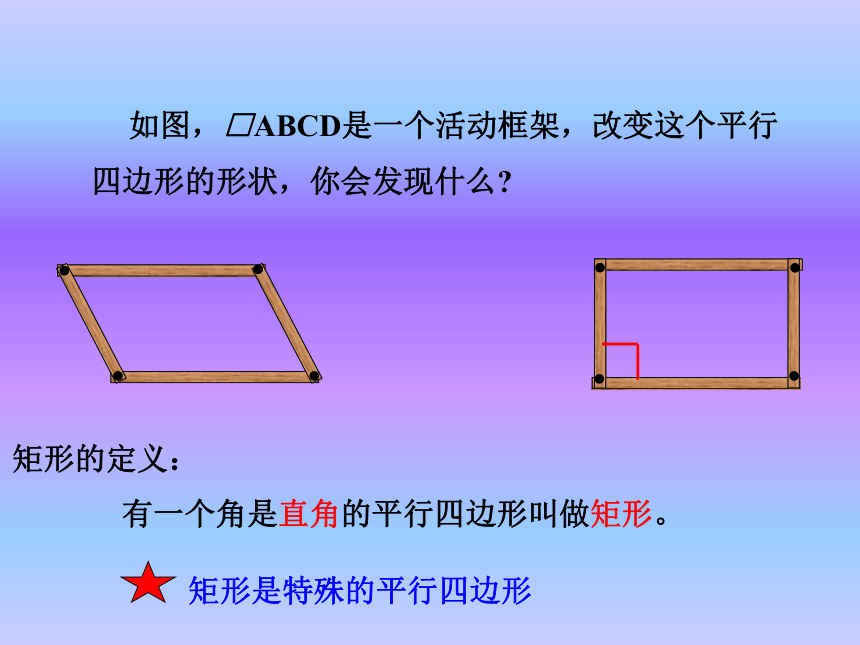
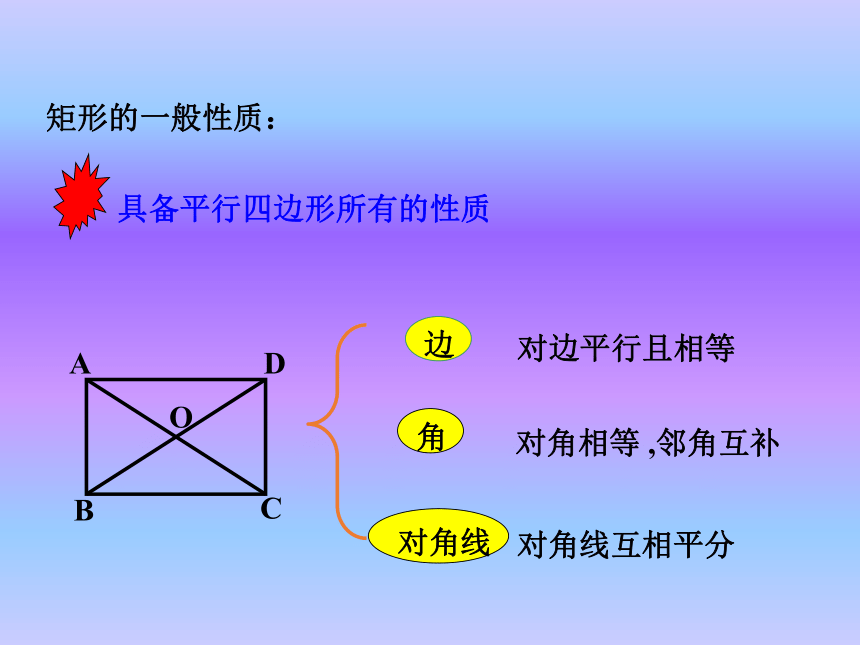
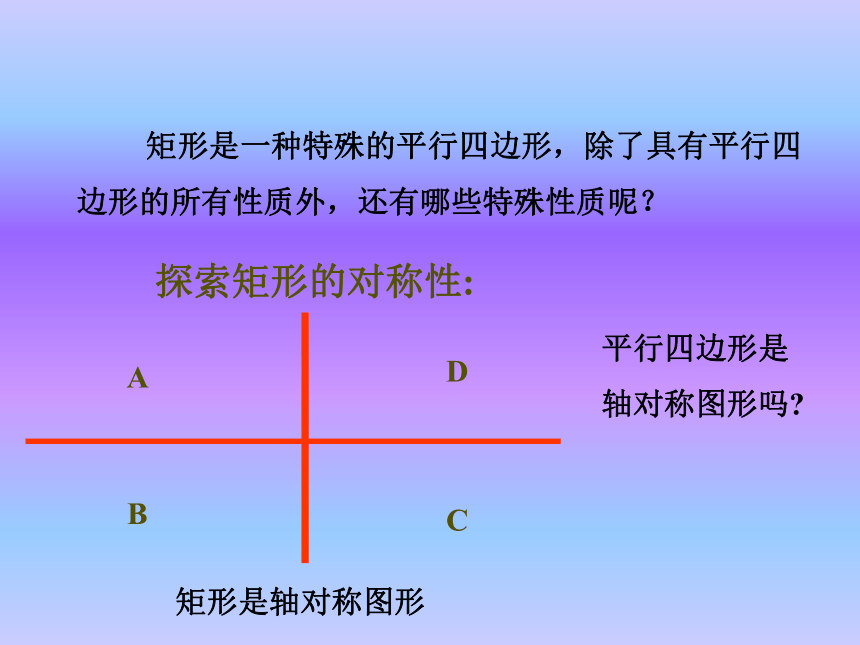
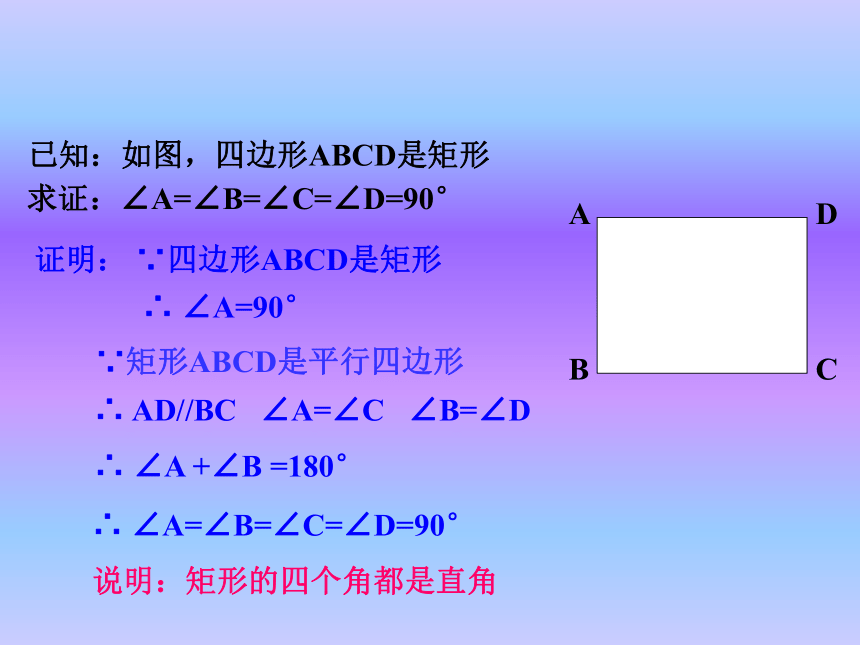
④对角线互相平分,即 AO=CO,BO=DO定义:把连接三角形两边中点的线段叫做三角形的中位线. 如图,□ABCD是一个活动框架,改变这个平行四边形的形状,你会发现什么?有一个角是直角的平行四边形叫做矩形。矩形的定义:对边平行且相等对角相等 ,邻角互补对角线互相平分矩形的一般性质:猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.自主探索对称性: 矩形既是轴对称图形,也是中心对称形.ABCD探索矩形的对称性: 矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?矩形是轴对称图形平行四边形是轴对称图形吗?已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°∵矩形ABCD是平行四边形∴ AD//BC ∠A=∠C ∠B=∠D
∴ ∠A +∠B =180°∴ ∠A=∠B=∠C=∠D=90°
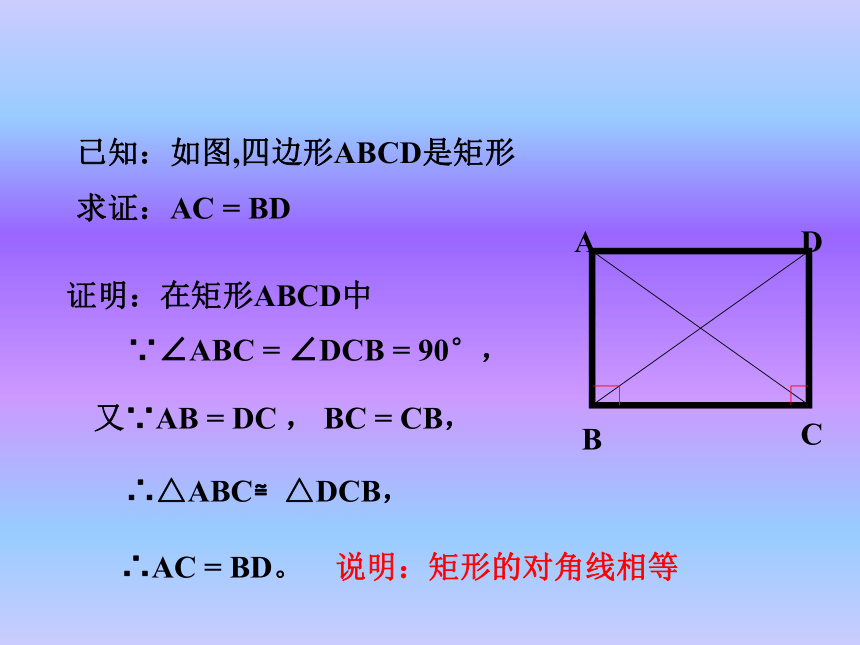
说明:矩形的四个角都是直角已知:如图,四边形ABCD是矩形
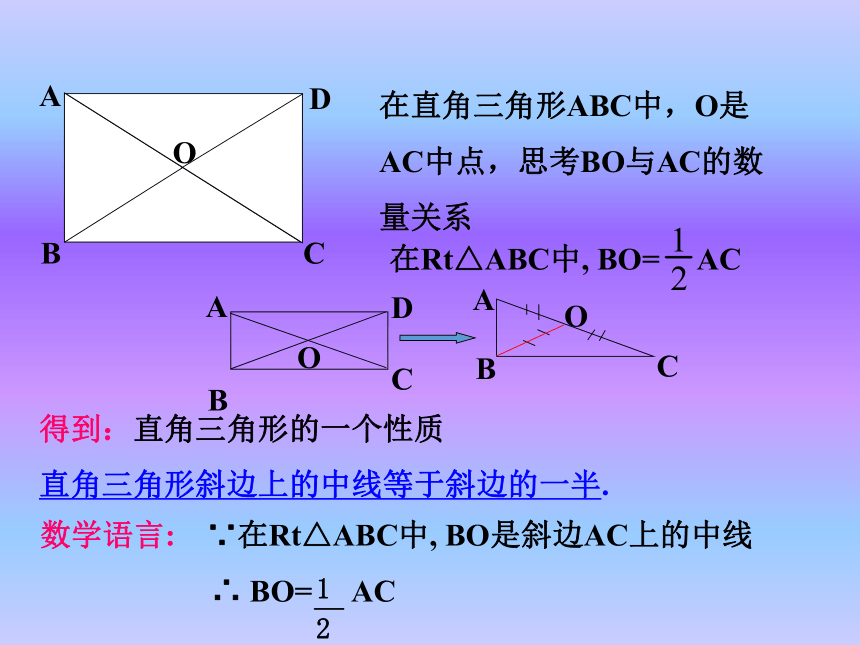
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°,又∵AB = DC , BC = CB,∴△ABC≌△DCB,∴AC = BD。 说明:矩形的对角线相等ABCO得到:直角三角形的一个性质
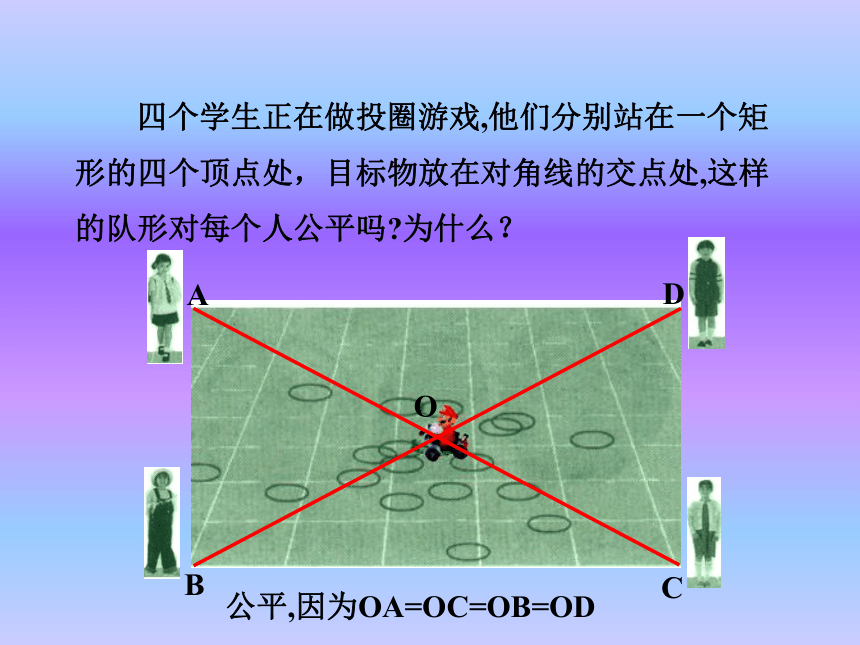
直角三角形斜边上的中线等于斜边的一半.在Rt△ABC中, BO= AC在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系ODOABCD公平,因为OA=OC=OB=OD例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4 cm,求矩形对角线的长.60°方法小结: 如果矩形两对角线的夹角是60°
或120°,那么其中必有等边三角形∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(cm)解:∵ 四边形ABCD是矩形×√×√√ 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 练习2 在“?”处填上恰当的条件: 练习3 已知:四边形ABCD是矩形
(1)若已知AB=8 cm,AD=6 cm,
则AC=_______ cm,
OB=_______cm
(2)若已知 ∠DOC=120°,AC=8 cm,则AD= _____cm,
AB= _____cm5104 直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴. 矩形的对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分矩形:有一个角是直角的平行四边形叫做矩形.第18章 平行四边形
18.2.1 矩形
第2课时 小明利用周末的时间,为自己做了一个相框. 问题1 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 创设情景 明确目标 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗?
1.掌握矩形的两个判定定理,能根据不同条件,选
取适当的定理进行推理计算;
2.经历矩形判定定理的猜想与证明过程,渗透类比
思想,体会类比学习和图形判定探究的一般思路.
学习目标 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?合作探究 达成目标证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? 练 习 ×√×√√ 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 探究点二 矩形判定的运用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数. 在“?”号处填上恰当的条件: 总结梳理 内化目标一种学习方法
两个猜想证明
三种判定方法 1.如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形 ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=
∴∠AOD=
又AO=DO ∴∠ADC=
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为达标检测 反思目标 2、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形
数学 八年级下册 人教版
第十八章 平行四边形
18.2.1 矩形
第1课时1.什么叫平行四边形?2.平行四边形有哪些性质?两组对边分别平行的四边形叫做平行四边形 .O①对边平行,即AD∥BC, AB∥CD
②对边相等, 即AB=CD, AD=BC
③对角相等,即∠A=∠ C,∠B=∠D
④对角线互相平分,即 AO=CO,BO=DO定义:把连接三角形两边中点的线段叫做三角形的中位线. 如图,□ABCD是一个活动框架,改变这个平行四边形的形状,你会发现什么?有一个角是直角的平行四边形叫做矩形。矩形的定义:对边平行且相等对角相等 ,邻角互补对角线互相平分矩形的一般性质:猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.自主探索对称性: 矩形既是轴对称图形,也是中心对称形.ABCD探索矩形的对称性: 矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?矩形是轴对称图形平行四边形是轴对称图形吗?已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°∵矩形ABCD是平行四边形∴ AD//BC ∠A=∠C ∠B=∠D
∴ ∠A +∠B =180°∴ ∠A=∠B=∠C=∠D=90°
说明:矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°,又∵AB = DC , BC = CB,∴△ABC≌△DCB,∴AC = BD。 说明:矩形的对角线相等ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.在Rt△ABC中, BO= AC在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系ODOABCD公平,因为OA=OC=OB=OD例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4 cm,求矩形对角线的长.60°方法小结: 如果矩形两对角线的夹角是60°
或120°,那么其中必有等边三角形∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(cm)解:∵ 四边形ABCD是矩形×√×√√ 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 练习2 在“?”处填上恰当的条件: 练习3 已知:四边形ABCD是矩形
(1)若已知AB=8 cm,AD=6 cm,
则AC=_______ cm,
OB=_______cm
(2)若已知 ∠DOC=120°,AC=8 cm,则AD= _____cm,
AB= _____cm5104 直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴. 矩形的对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分矩形:有一个角是直角的平行四边形叫做矩形.第18章 平行四边形
18.2.1 矩形
第2课时 小明利用周末的时间,为自己做了一个相框. 问题1 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 创设情景 明确目标 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗?
1.掌握矩形的两个判定定理,能根据不同条件,选
取适当的定理进行推理计算;
2.经历矩形判定定理的猜想与证明过程,渗透类比
思想,体会类比学习和图形判定探究的一般思路.
学习目标 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?合作探究 达成目标证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? 练 习 ×√×√√ 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 探究点二 矩形判定的运用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数. 在“?”号处填上恰当的条件: 总结梳理 内化目标一种学习方法
两个猜想证明
三种判定方法 1.如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形 ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=
∴∠AOD=
又AO=DO ∴∠ADC=
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为达标检测 反思目标 2、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形
