人教版八年级数学下册课件19.1.2 函数的图像 课件(34张PPT 2课时)
文档属性
| 名称 | 人教版八年级数学下册课件19.1.2 函数的图像 课件(34张PPT 2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 777.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 00:00:00 | ||
图片预览








文档简介
课件34张PPT。教学课件
数学 八年级下册 人教版
第十九章 一次函数
19.1.2 函数的图像
第1课时 分别指出下列各关系式中的变量与常量:(1)三角形的一边长5cm,它的面积s(cm )与
这边上的高h(cm)的关系式是s= h;(2)如果直角三角形中一个锐角的度数为α,那
么另一个锐角的度数β与α间的关系式是
β=90-α;(3)如果某种报纸的单价为8元,x表示购买这种
报纸的份数,那么购买报纸的总价y(元)与x
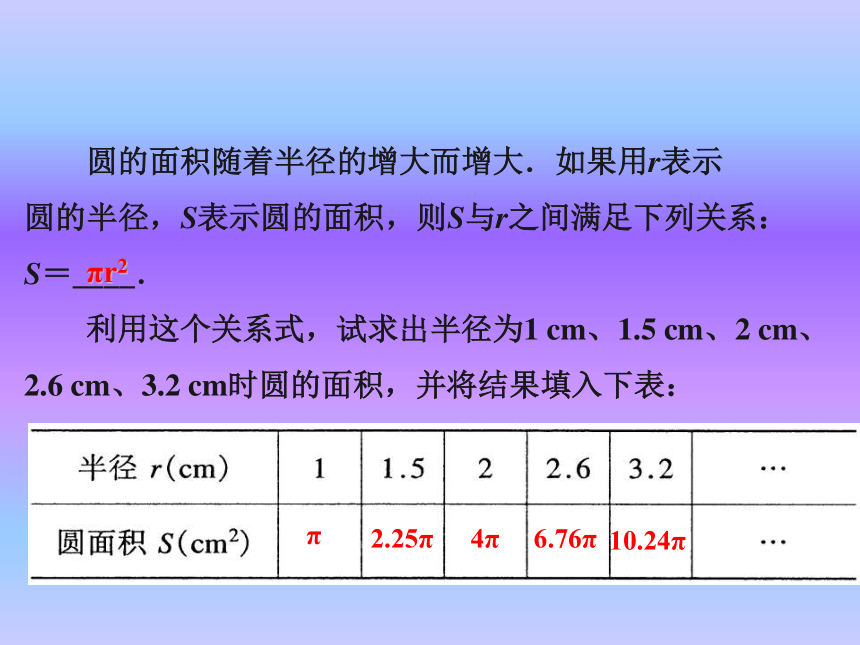
间的关系是y=8x.2 圆的面积随着半径的增大而增大.如果用r表示
圆的半径,S表示圆的面积,则S与r之间满足下列关系:
S=____.
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、
2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
2.25ππ4π6.76π10.24ππr2新课引入
在平面直角坐标系中,平面内的点可以用一对
来表示.即坐标平面内的 ___ 与有
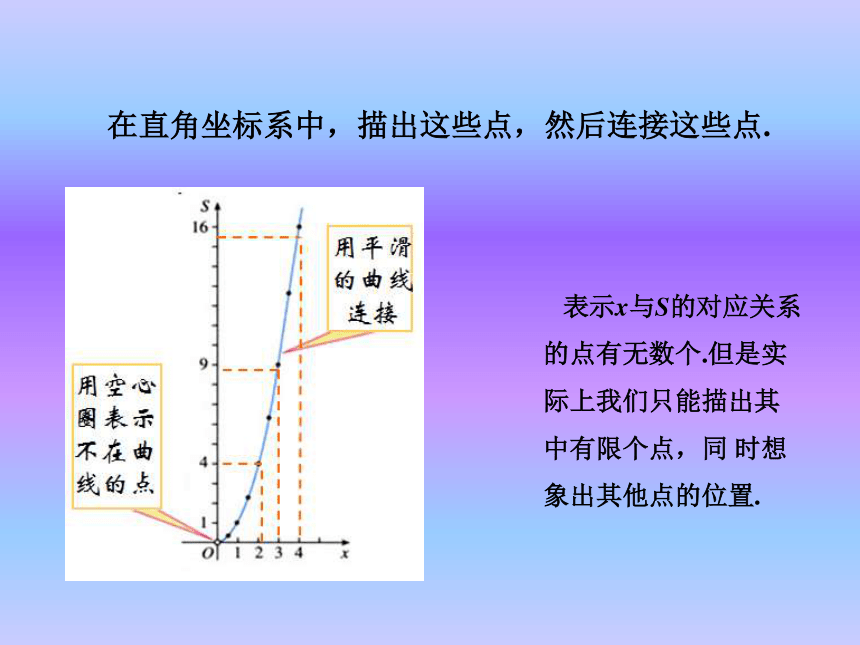
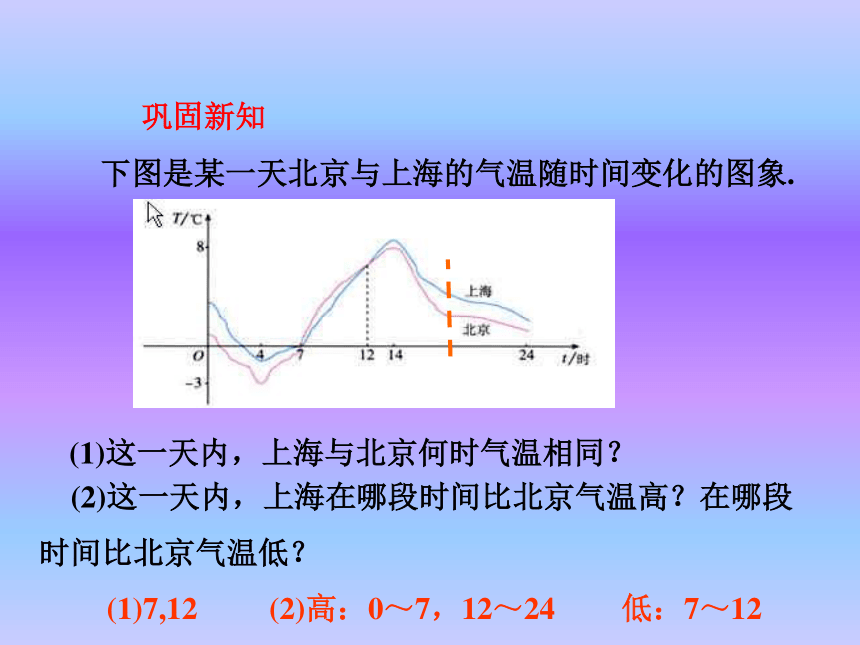
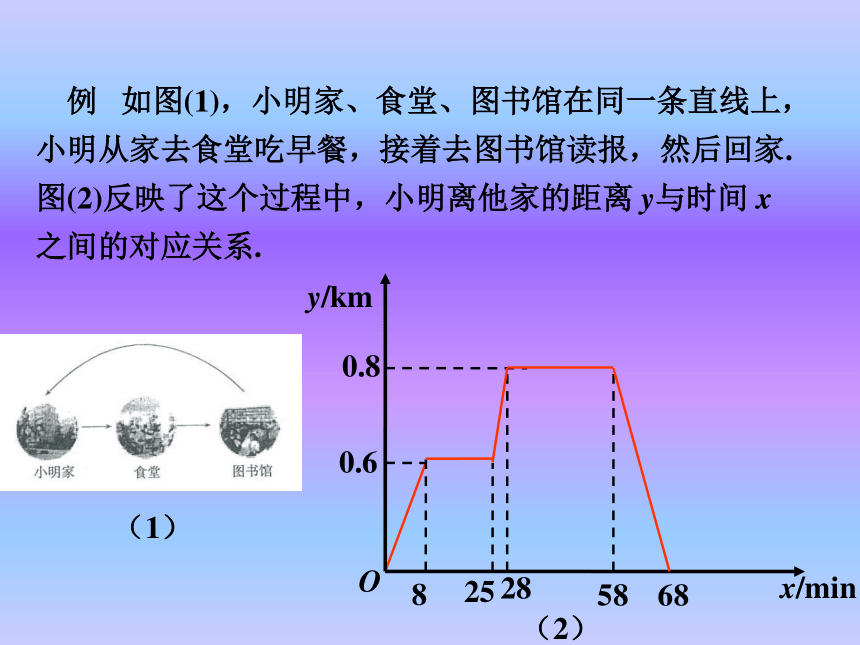
序数对是一一________ 的.有序数对点对应探究新知 问题:写出正方形的面积S与边长x的函数解析式,并确定自变量x的取值范围.S=x2(x>0)00.2512.2546.25912.2516在直角坐标系中,描出这些点,然后连接这些点. 表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同 时想象出其他点的位置. 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.上图的曲线即函数S=x2 (x>0)的图象. 通过图象,我们可以数形结合地研究函数. 下图是某一天北京与上海的气温随时间变化的图象.(1)这一天内,上海与北京何时气温相同? (2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?(1)7,12(2)高:0~7,12~24低:7~12巩固新知 例 如图(1),小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图(2)反映了这个过程中,小明离他家的距离 y与时间 x之间的对应关系.(1)(2)根据图象回答下列问题: (1)食堂离小明家多远?小明从家到食堂用了多少时间?(2)小明吃早餐用了多少时间? (3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?食堂离小明家0.6km,小明走到食堂用了8min.小明吃早餐用了17min. 食堂离图使馆0.2km,小明从食堂到图书馆用了3min.(4)小明读报用了多少时间? (5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少? 分析:小明离家的距离y是时间x的函数,从图象中有两段是平行于x轴的线段可知,小明离家后又两段时间内先后停留在食堂与图书馆.小明读报用了30min. 图书馆离小明家0.8km,小明从图书馆回家的平均速度0.08km/min. 在下列式子中,对于x每一确定的值,y有唯一的对应值,即y是x的函数,你能画出这些函数的图象吗?(1)y=x+0.5;(1)解:1.列表.2.描点.3.连线. O-11xyy=x+0.5直线由左向右上升,即当x由小变大时,y=x+5随之增大.-2.5-0.50.51.52.53.5-1.51-1(2)解:1.列表.2.描点.3.连线. 曲线 从左向右下降,即当x由小变大时,随之减小.6321.51 (1)函数图象会使函数关系更为清晰,怎样画出函数
的图象呢?(2)如何根据函数图象中获得的信息来研究实际问题?(3)画函数图象的三个步骤分别是什么?(4)如何从图象中了解函数的变化情况?第十九章 一次函数
19.1.2 函数的图像
第2课时 1、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?为什么?如果能,请写出它们的关系式。(1)每一个同学购一本代数书,书的单价为2元,则 x 个同学共付 y 元。(2)计划购买50元的乒乓球,则所购的总数 y(个)与单价 x (元)的关系。(3)一个铜球在0 ℃的体积为1000cm3,加热后温度每增加1℃,体积增加0.051cm3,t ℃时球的体积为 V cm3 。解: y 是 x 的函数.其关系式为y = 2x (x ≥0)解: y 是 x 的函数.其关系式为y =(x>0)解: v是 t 的函数,其关系式为V = 0.051t+10002、下图是某一天北京与上海的气温随时间变化的图象.
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?答:7时 和 12时。0时-7时和12时-24时;7时—12时。 学习目标:
1.了解函数的三种表示法及其优缺点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.
学习重点:
综合运用三种表示法表示函数关系,研究运动变化
过程. 问题1:有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表:受力后弹簧的长度l是所挂重物m的函数吗?是 11.7511.51110.510 问题2:有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了t(t>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?是 y=2x+2问题3:下图是某地某一天的气温变化图. (1)指出其中的两个变量是 , .
(2)其中 是 的函数,自变量是 .气温T时间t气温T时间t时间t 问题4:从上面的三个问题中,可以发现表示函数有哪三种方法,这三种表示函数的方法各有什么优缺点?在遇到具体问题时,该如何选择适当的表示方法呢?问题1:表示函数有哪三种方法?列表法、解析式法和图象法.问题2:这三种表示的方法各有什么优点? 列表法比较直观、准确地表示出函数中两个变量之间的关系; 解析式法比较准确、全面地表示出函数中两个变量之间的关系; 图象法比较形象、直观地表示出函数中两个变量之间的关系.问题3:这三种表示的方法各有什么不足之处呢? 问题4:请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表: 从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.√××××××√√√√√活动 函数的三种表示方法之间的转化 问题:一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水温高度. (1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位变化的规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将为多少米.y=0.3x+3是水位越来越高是 1. 用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数. 解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下: 所以m=(n-2)·180°(n≥3,且n为自然数).180360540720 2. 用解析式法与图象法表示等边三角形的周长l是边长a的函数. 解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).描点、连线:用描点法画函数l=3a的图象. 3.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y( ℃ )与上升高度 x(m)之间的函数关系式 ,若某种植物适宜生长的度为17 ℃
数学 八年级下册 人教版
第十九章 一次函数
19.1.2 函数的图像
第1课时 分别指出下列各关系式中的变量与常量:(1)三角形的一边长5cm,它的面积s(cm )与
这边上的高h(cm)的关系式是s= h;(2)如果直角三角形中一个锐角的度数为α,那
么另一个锐角的度数β与α间的关系式是
β=90-α;(3)如果某种报纸的单价为8元,x表示购买这种
报纸的份数,那么购买报纸的总价y(元)与x
间的关系是y=8x.2 圆的面积随着半径的增大而增大.如果用r表示
圆的半径,S表示圆的面积,则S与r之间满足下列关系:
S=____.
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、
2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
2.25ππ4π6.76π10.24ππr2新课引入
在平面直角坐标系中,平面内的点可以用一对
来表示.即坐标平面内的 ___ 与有
序数对是一一________ 的.有序数对点对应探究新知 问题:写出正方形的面积S与边长x的函数解析式,并确定自变量x的取值范围.S=x2(x>0)00.2512.2546.25912.2516在直角坐标系中,描出这些点,然后连接这些点. 表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同 时想象出其他点的位置. 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.上图的曲线即函数S=x2 (x>0)的图象. 通过图象,我们可以数形结合地研究函数. 下图是某一天北京与上海的气温随时间变化的图象.(1)这一天内,上海与北京何时气温相同? (2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?(1)7,12(2)高:0~7,12~24低:7~12巩固新知 例 如图(1),小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图(2)反映了这个过程中,小明离他家的距离 y与时间 x之间的对应关系.(1)(2)根据图象回答下列问题: (1)食堂离小明家多远?小明从家到食堂用了多少时间?(2)小明吃早餐用了多少时间? (3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?食堂离小明家0.6km,小明走到食堂用了8min.小明吃早餐用了17min. 食堂离图使馆0.2km,小明从食堂到图书馆用了3min.(4)小明读报用了多少时间? (5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少? 分析:小明离家的距离y是时间x的函数,从图象中有两段是平行于x轴的线段可知,小明离家后又两段时间内先后停留在食堂与图书馆.小明读报用了30min. 图书馆离小明家0.8km,小明从图书馆回家的平均速度0.08km/min. 在下列式子中,对于x每一确定的值,y有唯一的对应值,即y是x的函数,你能画出这些函数的图象吗?(1)y=x+0.5;(1)解:1.列表.2.描点.3.连线. O-11xyy=x+0.5直线由左向右上升,即当x由小变大时,y=x+5随之增大.-2.5-0.50.51.52.53.5-1.51-1(2)解:1.列表.2.描点.3.连线. 曲线 从左向右下降,即当x由小变大时,随之减小.6321.51 (1)函数图象会使函数关系更为清晰,怎样画出函数
的图象呢?(2)如何根据函数图象中获得的信息来研究实际问题?(3)画函数图象的三个步骤分别是什么?(4)如何从图象中了解函数的变化情况?第十九章 一次函数
19.1.2 函数的图像
第2课时 1、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?为什么?如果能,请写出它们的关系式。(1)每一个同学购一本代数书,书的单价为2元,则 x 个同学共付 y 元。(2)计划购买50元的乒乓球,则所购的总数 y(个)与单价 x (元)的关系。(3)一个铜球在0 ℃的体积为1000cm3,加热后温度每增加1℃,体积增加0.051cm3,t ℃时球的体积为 V cm3 。解: y 是 x 的函数.其关系式为y = 2x (x ≥0)解: y 是 x 的函数.其关系式为y =(x>0)解: v是 t 的函数,其关系式为V = 0.051t+10002、下图是某一天北京与上海的气温随时间变化的图象.
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?答:7时 和 12时。0时-7时和12时-24时;7时—12时。 学习目标:
1.了解函数的三种表示法及其优缺点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.
学习重点:
综合运用三种表示法表示函数关系,研究运动变化
过程. 问题1:有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表:受力后弹簧的长度l是所挂重物m的函数吗?是 11.7511.51110.510 问题2:有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了t(t>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?是 y=2x+2问题3:下图是某地某一天的气温变化图. (1)指出其中的两个变量是 , .
(2)其中 是 的函数,自变量是 .气温T时间t气温T时间t时间t 问题4:从上面的三个问题中,可以发现表示函数有哪三种方法,这三种表示函数的方法各有什么优缺点?在遇到具体问题时,该如何选择适当的表示方法呢?问题1:表示函数有哪三种方法?列表法、解析式法和图象法.问题2:这三种表示的方法各有什么优点? 列表法比较直观、准确地表示出函数中两个变量之间的关系; 解析式法比较准确、全面地表示出函数中两个变量之间的关系; 图象法比较形象、直观地表示出函数中两个变量之间的关系.问题3:这三种表示的方法各有什么不足之处呢? 问题4:请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表: 从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.√××××××√√√√√活动 函数的三种表示方法之间的转化 问题:一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水温高度. (1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位变化的规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将为多少米.y=0.3x+3是水位越来越高是 1. 用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数. 解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下: 所以m=(n-2)·180°(n≥3,且n为自然数).180360540720 2. 用解析式法与图象法表示等边三角形的周长l是边长a的函数. 解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).描点、连线:用描点法画函数l=3a的图象. 3.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y( ℃ )与上升高度 x(m)之间的函数关系式 ,若某种植物适宜生长的度为17 ℃
