2019-2020学年上海市九年级数学第一学期期末考试复习试卷(解析版)
文档属性
| 名称 | 2019-2020学年上海市九年级数学第一学期期末考试复习试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-16 17:18:22 | ||
图片预览


文档简介
2019-2020学年上海市九年级数学第一学期期末考试复习试卷
一.选择题(共6小题,满分24分,每小题4分)
1.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
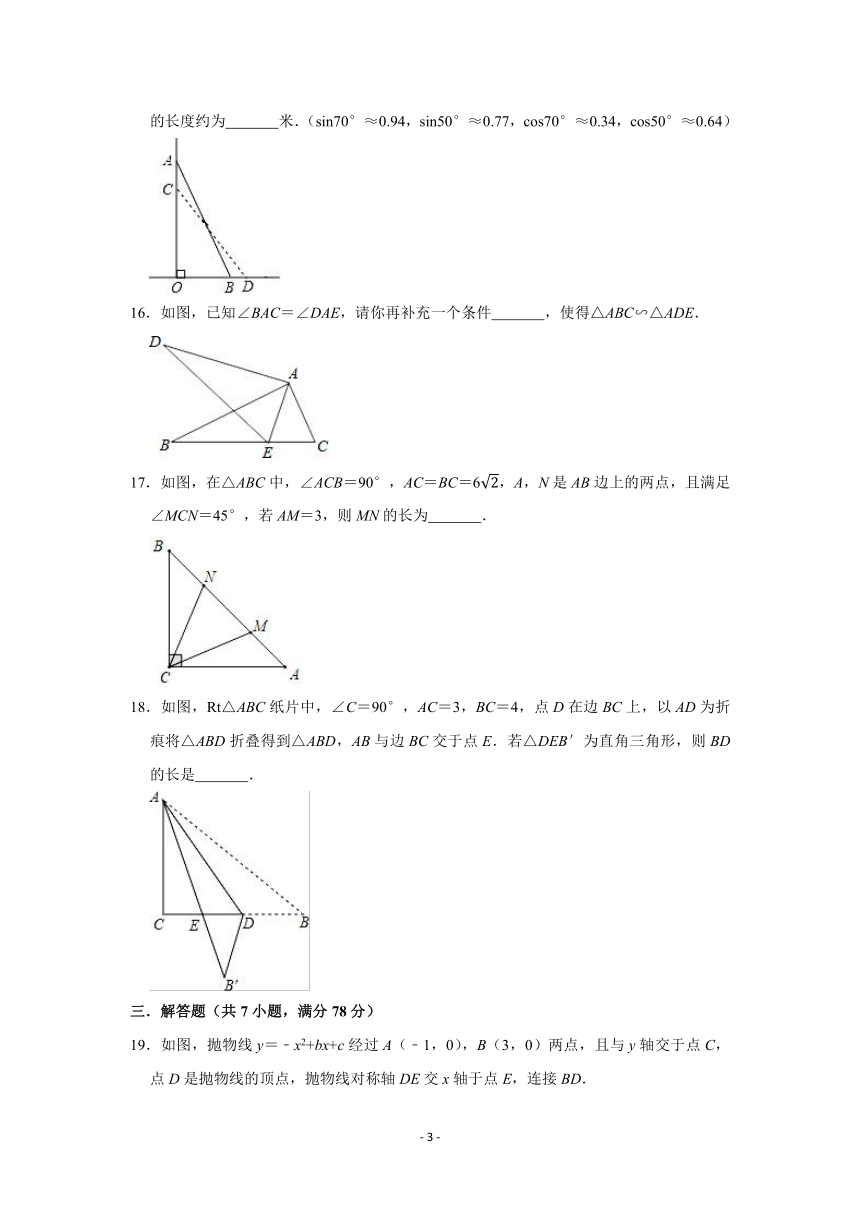
2.如图,在一次活动中,位于A处的七年一班准备前往相距3km的B处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
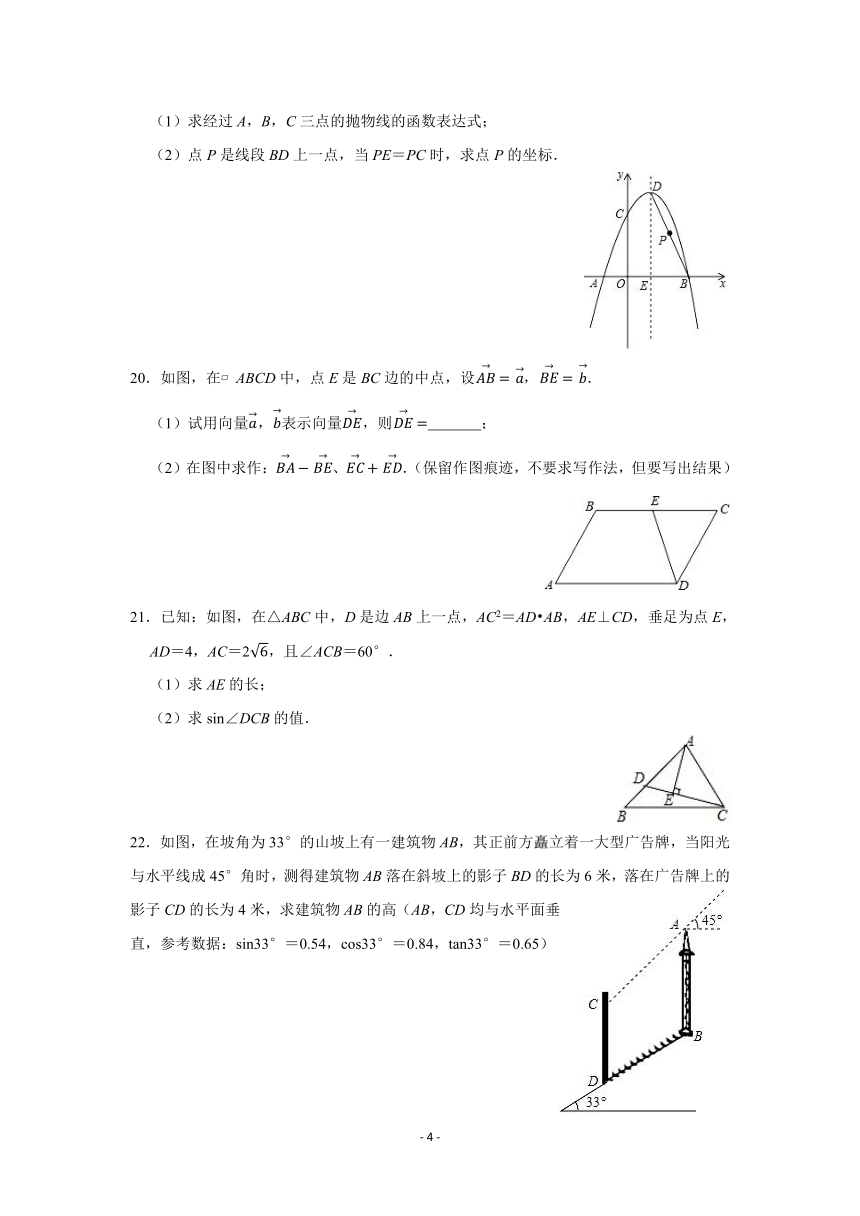
A.南偏西30°,3km B.南偏西50°,3km
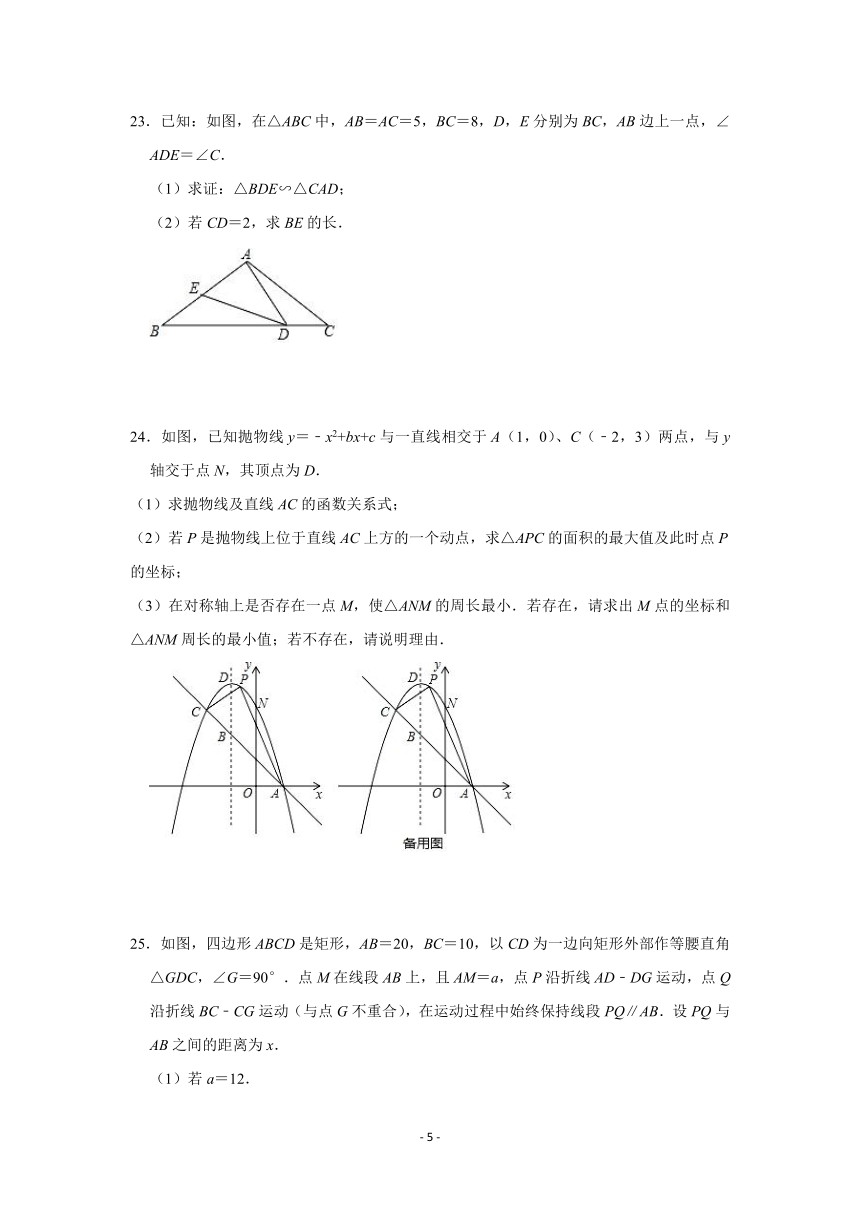
C.北偏东40°,3km D.北偏东50°,3km
3.抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先向右平移3个单位,再向上平移2个单位
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①abc>0;②9a+3b+c=0;③b2﹣4ac<8a;④5a+b+c>0.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.已知、和都是非零向量,在下列选项中,不能判定的是( )
A., B.||=|| C. D.,
6.在△ABC中,E、F是BC边上的三等分点,BM是AC边上的中线,AE、AF分BM为三段的长分别是x、y、z,若这三段有x>y>z,则x:y:z等于( )
A.3:2:1 B.4:2:1 C.5:2:1 D.5:3:2
二.填空题(共12小题,满分48分,每小题4分)
7.已知2x=5y,那么 .
8.计算:3(2)﹣2(3)= .
9.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .
10.抛物线y=2x2﹣4x﹣3,当﹣1≤x≤4时,y的取值范围是 .
11.如图,E、F是线段AB的两个黄金分割点,AB=1,则线段EF的长为 .(结果保留根号)
12.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 .
13.当两个相似三角形的相似比为 时,这两个相似三角形的面积比是1:2.
14.在Rt△ABC中,∠ACB=90°,若tanA=3,AB,则BC=
15.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
16.如图,已知∠BAC=∠DAE,请你再补充一个条件 ,使得△ABC∽△ADE.
17.如图,在△ABC中,∠ACB=90°,AC=BC=6,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为 .
18.如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△ABD,AB与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
三.解答题(共7小题,满分78分)
19.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
20.如图,在?ABCD中,点E是BC边的中点,设,.
(1)试用向量,表示向量,则 ;
(2)在图中求作:、.(保留作图痕迹,不要求写作法,但要写出结果)
21.已知:如图,在△ABC中,D是边AB上一点,AC2=AD?AB,AE⊥CD,垂足为点E,AD=4,AC=2,且∠ACB=60°.
(1)求AE的长;
(2)求sin∠DCB的值.
22.如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
23.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
25.如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.
(1)若a=12.
①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为 ;
②在运动过程中,求四边形AMQP的最大面积;
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.
2019-2020学年上海市九年级数学第一学期期末考试复习试卷
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
【解答】解:如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC,
故选:C.
2.如图,在一次活动中,位于A处的七年一班准备前往相距3km的B处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
A.南偏西30°,3km B.南偏西50°,3km
C.北偏东40°,3km D.北偏东50°,3km
【解答】解;用方向和距离描述七年二班相对于七年一班的位置为:南偏西30°,AB=3km,
故选:A.
3.抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先向右平移3个单位,再向上平移2个单位
【解答】解:因为y=x2+6x+7=(x+3)2﹣2.
所以将抛物线y=x2先向左平移3个单位,再向下平移2个单位即可得到抛物线y=x2+6x+7.
故选:A.
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①abc>0;②9a+3b+c=0;③b2﹣4ac<8a;④5a+b+c>0.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①由图象可知:a>0,c<0,
∴由于对称轴0,
∴b<0,
∴abc>0,故①正确;
②抛物线过(3,0),
∴x=3,y=9a+3b+c=0,故②正确;
③顶点坐标为:(,)
由图象可知:2,
∵a>0,
∴4ac﹣b2<﹣8a,
即b2﹣4ac>8a,故③错误;
④由图象可知:1,a>0,
∴2a+b<0,
∵9a+3b+c=0,
∴c=﹣9a﹣3b,
∴5a+b+c=5a+b﹣9a﹣3b=﹣4a﹣2b=﹣2(2a+b)>0,故④正确;
故选:C.
5.已知、和都是非零向量,在下列选项中,不能判定的是( )
A., B.||=|| C. D.,
【解答】解:A、∵,,∴,故本选项错误;
B、∵||=||,∴与的模相等,但不一定平行,故本选项正确;
C、∵,∴,故本选项错误;
D、∵,,∴,故本选项错误.
故选:B.
6.在△ABC中,E、F是BC边上的三等分点,BM是AC边上的中线,AE、AF分BM为三段的长分别是x、y、z,若这三段有x>y>z,则x:y:z等于( )
A.3:2:1 B.4:2:1 C.5:2:1 D.5:3:2
【解答】解:如图,作MH∥BC交AE于H,交AF于G,设AE交BM于K,AF交BM于J.
∵MH∥BC,
∴,
∵BE=EF=CF,
∴HG=MGCF,
∴,
∴y+z=x,
∴,
∴x+y=4z,
∴xz,yz,
∴x:y:z=5:3:2,
故选:D.
二.填空题(共12小题,满分48分,每小题4分)
7.已知2x=5y,那么 .
【解答】解:∵2x=5y,
∴设x=5a,则y=2a,
那么.
故答案为:.
8.计算:3(2)﹣2(3)= .
【解答】解:3(2)﹣2(3)
=3323
=(3﹣2)(﹣3+3)
.
故答案是:.
9.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 ﹣1 .
【解答】解:∵二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,
∴a2﹣1=0,
∴a=±1,
∵a﹣1≠0,
∴a≠1,
∴a的值为﹣1.
故答案为:﹣1.
10.抛物线y=2x2﹣4x﹣3,当﹣1≤x≤4时,y的取值范围是 ﹣5≤y≤13 .
【解答】解:∵y=2x2﹣4x﹣3
=2(x2﹣2x)﹣3,
=2(x2﹣2x+1﹣1)﹣3,
=2(x﹣1)2﹣5,
∴当x=1时,y最小值=﹣5,
∵﹣1≤x≤4,且|4﹣1>|﹣1﹣1|,
∴x=4时,y最大=13,
∴当﹣1≤x≤4时,y的取值范围是:﹣5≤y≤13.
故答案为﹣5≤y≤13.
11.如图,E、F是线段AB的两个黄金分割点,AB=1,则线段EF的长为 2 .(结果保留根号)
【解答】解:∵E、F是线段AB的两个黄金分割点,
∴AF=BEAB,
∴EF=AF+BE﹣AB2,
故答案为:2.
12.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 15 .
【解答】解:∵AB∥CD,
∴△ABE∽△DCE,
∴,
∴,
∵EF∥CD,
∴△BEF∽△BCD,
∴,
∵EF=6,
∴CD=15,
故答案为15.
13.当两个相似三角形的相似比为 1: 时,这两个相似三角形的面积比是1:2.
【解答】解:∵相似三角形的面积比等于相似比的平方,
∴两个相似三角形的面积比是1:2时,两个相似三角形的相似比为:1:.
故答案为:1:.
14.在Rt△ABC中,∠ACB=90°,若tanA=3,AB,则BC= 3
【解答】解:∵在Rt△ABC中,tanA3,
∴设BC=3x,则AC=x,
由BC2+AC2=AB2可得9x2+x2=10,
解得:x=1(负值舍去),
则BC=3,
故答案为:3.
15.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 1.02 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解答】解:由题意可得:
∵∠ABO=70°,AB=6m,
∴sin70°0.94,
解得:AO=5.64(m),
∵∠CDO=50°,DC=6m,
∴sin50°0.77,
解得:CO=4.62(m),
则AC=5.64﹣4.62=1.02(m),
答:AC的长度约为1.02米.
故答案为:1.02.
16.如图,已知∠BAC=∠DAE,请你再补充一个条件 ∠B=∠D等 ,使得△ABC∽△ADE.
【解答】解:∵∠BAC=∠DAE,
∠B=∠D,
∴△ABC∽△ADE,
故答案为:∠B=∠D等
17.如图,在△ABC中,∠ACB=90°,AC=BC=6,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为 5 .
【解答】解:如图,将△CBN顺时针旋转90度,得到△ACR,连接RM
则△CRA≌△CNB全等,
∴AR=BN,∠B=∠CAR,∠BCN=∠ACR,
∵∠ACB=90°,AC=BC=6,
∴AB=12,∠B=∠CAB=45°,
∴∠CAR=45°,
∴∠MAR=90°,
∵∠MCN=45°,
∴∠BCN+∠ACM=45°=∠ACM+∠ACR,
∴∠MCN=∠MCR,且CN=CR,CM=CM,
∴△CNM≌△CRM(SAS)
∴MN=MR,
∵AB=12,AM=3,
∴BN+MN=9,
∴BN=AR=9﹣MN,
∵MR2=AM2+AR2,
∴MN2=(9﹣MN)2+9,
∴MN=5
故答案为5.
18.如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△ABD,AB与边BC交于点E.若△DEB′为直角三角形,则BD的长是 1或 .
【解答】解:(1)当∠EDB′=90°时,如图1所示:
由折叠得:∠B=∠B′,BD=B′D,
在Rt△ABC中,AB5,
∵∠AEC=∠DEB′,∠C=∠EDB′=90°,
∴∠B=∠B′=∠CAE,
∴△ACE∽△BCA,
∴,即:,
∴CE,AE,
∴BE=5,
设BD=x=B′D,则DE=4xx,
在Rt△DEB′中,由勾股定理得:
()2=x2+(x)2,
解得:x1=1,x21(舍去),
(2)当∠DEB′=90°时,此时点E与点C重合,如图2所示:
由折叠得,AB=AB′=5,
∴EB′=5﹣3=2,设BD=x,则B′D=x,ED=4﹣x
在Rt△DEB′中,由勾股定理得:
x2=22+(4﹣x)2,解得:x,
故答案为:1或.
三.解答题(共7小题,满分78分)
19.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
【解答】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴,解得,
∴所求的抛物线的函数表达式为y=﹣x2+2x+3;
(2)如图,连接PC,PE.
抛物线的对称轴为x1.
当x=1时,y=4,
∴点D的坐标为(1,4).
设直线BD的解析式为y=kx+b,
则,
解得.
∴直线BD的解析式为:y=﹣2x+6,
设点P的坐标为(x,﹣2x+6),又C(0,3),E(1,0),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,
∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,
解得,x=2,
则y=﹣2×2+6=2,
∴点P的坐标为(2,2).
20.如图,在?ABCD中,点E是BC边的中点,设,.
(1)试用向量,表示向量,则 . ;
(2)在图中求作:、.(保留作图痕迹,不要求写作法,但要写出结果)
【解答】解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是BC的中点,
∴BE=EC,
∵,,,
∴.
故答案为:.
(2)如图,,.
向量,向量即为所求.
21.已知:如图,在△ABC中,D是边AB上一点,AC2=AD?AB,AE⊥CD,垂足为点E,AD=4,AC=2,且∠ACB=60°.
(1)求AE的长;
(2)求sin∠DCB的值.
【解答】解:(1)∵AC2=AD?AB,∴,
∵∠DAC∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB=60°,∠ACD=∠ABC,
∵∠AED=90°,AD=4,
∴DE=2,
∴AE2;
(2)∵,AC2=AD?AB,
∴AB,
∴EC2,
∴∠ACD=45°,
∴∠ABC=∠ACD=45°,
过点D作DF⊥BC,垂足为F,
∴BF=DF=2,
∵DC=DE+CE=2+2,
∴sin∠DCB.
22.如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
【解答】解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,
在Rt△BFD中,sin∠DBF,
则DF=BD?sin∠DBF≈6×0.54=3.24,
cos∠DBF,
则BF=BD?cos∠DBF≈6×0.84=5.04,
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=5.04,CF=BE=CD﹣DF=4﹣3.24=0.76,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=5.04,
∴AB=AE+BE=5.04+0.76=5.8,
答:建筑物AB的高约为5.8m.
23.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE=∠C,∠DAE=∠BAD,
∴∠ADE=∠B,
∴∠AED=∠ADB.
∵∠BED+∠AED=∠CDA+∠ADB=180°,
∴∠BED=∠CDA,
∴△BDE∽△CAD.
(2)解∵AB=AC=5,BC=8,CD=2,
∴BD=6.
∵△BDE∽△CAD,
∴,即,
∴BE.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
【解答】解:(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,
PF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APCAQ?PFx2x+3(x)2.
∵0,
∴当x时,△APC的面积取最大值,最大值为,此时点P的坐标为(,).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC3,AN,
∴C△ANM=AM+MN+AN=AC+AN=3.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
25.如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.
(1)若a=12.
①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为 3 ;
②在运动过程中,求四边形AMQP的最大面积;
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.
【解答】(1)解:①P在线段AD上,PQ=AB=20,AP=x,AM=12,
四边形AMQP的面积(12+20)x=48,
解得:x=3;
故答案为:3;
②当P,在AD上运动时,P到D点时四边形AMQP面积最大,为直角梯形,
∴0<x≤10时,四边形AMQP面积的最大值(12+20)10=160,
当P在DG上运动,10<x<20,四边形AMQP为不规则梯形,
作PK⊥AB于K,交CD于N,作GE⊥CD于E,交AB于F,如图2所示:
则PK=x,PN=x﹣10,EF=BC=10,
∵△GDC是等腰直角三角形,
∴DE=CE,GECD=10,
∴GF=GE+EF=20,
∴GH=20﹣x,
由题意得:PQ∥CD,
∴△GPQ∽△GDC,
∴,
即,
解得:PQ=40﹣2x,
∴梯形AMQP的面积(12+40﹣2x)×x=﹣x2+26x=﹣(x﹣13)2+169,
∴当x=13时,四边形AMQP的面积最大=169;
(2)解:P在DG上,则10≤x<20,AM=a,PQ=40﹣2x,
梯形AMQP的面积S(a+40﹣2x)×x=﹣x2x,对称轴为:x=10,
∵0≤a≤20,
∴10≤1015,对称轴在10和15之间,
∵10≤x<20,二次函数图象开口向下,
∴当x无限接近于20时,S最小,
∴﹣20220≥50,
∴a≥5;
综上所述,a的取值范围为5≤a≤20.
(
1
)
一.选择题(共6小题,满分24分,每小题4分)
1.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
2.如图,在一次活动中,位于A处的七年一班准备前往相距3km的B处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
A.南偏西30°,3km B.南偏西50°,3km
C.北偏东40°,3km D.北偏东50°,3km
3.抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先向右平移3个单位,再向上平移2个单位
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①abc>0;②9a+3b+c=0;③b2﹣4ac<8a;④5a+b+c>0.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.已知、和都是非零向量,在下列选项中,不能判定的是( )
A., B.||=|| C. D.,
6.在△ABC中,E、F是BC边上的三等分点,BM是AC边上的中线,AE、AF分BM为三段的长分别是x、y、z,若这三段有x>y>z,则x:y:z等于( )
A.3:2:1 B.4:2:1 C.5:2:1 D.5:3:2
二.填空题(共12小题,满分48分,每小题4分)
7.已知2x=5y,那么 .
8.计算:3(2)﹣2(3)= .
9.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .
10.抛物线y=2x2﹣4x﹣3,当﹣1≤x≤4时,y的取值范围是 .
11.如图,E、F是线段AB的两个黄金分割点,AB=1,则线段EF的长为 .(结果保留根号)
12.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 .
13.当两个相似三角形的相似比为 时,这两个相似三角形的面积比是1:2.
14.在Rt△ABC中,∠ACB=90°,若tanA=3,AB,则BC=
15.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
16.如图,已知∠BAC=∠DAE,请你再补充一个条件 ,使得△ABC∽△ADE.
17.如图,在△ABC中,∠ACB=90°,AC=BC=6,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为 .
18.如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△ABD,AB与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
三.解答题(共7小题,满分78分)
19.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
20.如图,在?ABCD中,点E是BC边的中点,设,.
(1)试用向量,表示向量,则 ;
(2)在图中求作:、.(保留作图痕迹,不要求写作法,但要写出结果)
21.已知:如图,在△ABC中,D是边AB上一点,AC2=AD?AB,AE⊥CD,垂足为点E,AD=4,AC=2,且∠ACB=60°.
(1)求AE的长;
(2)求sin∠DCB的值.
22.如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
23.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
25.如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.
(1)若a=12.
①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为 ;
②在运动过程中,求四边形AMQP的最大面积;
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.
2019-2020学年上海市九年级数学第一学期期末考试复习试卷
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
【解答】解:如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC,
故选:C.
2.如图,在一次活动中,位于A处的七年一班准备前往相距3km的B处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
A.南偏西30°,3km B.南偏西50°,3km
C.北偏东40°,3km D.北偏东50°,3km
【解答】解;用方向和距离描述七年二班相对于七年一班的位置为:南偏西30°,AB=3km,
故选:A.
3.抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先向右平移3个单位,再向上平移2个单位
【解答】解:因为y=x2+6x+7=(x+3)2﹣2.
所以将抛物线y=x2先向左平移3个单位,再向下平移2个单位即可得到抛物线y=x2+6x+7.
故选:A.
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①abc>0;②9a+3b+c=0;③b2﹣4ac<8a;④5a+b+c>0.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①由图象可知:a>0,c<0,
∴由于对称轴0,
∴b<0,
∴abc>0,故①正确;
②抛物线过(3,0),
∴x=3,y=9a+3b+c=0,故②正确;
③顶点坐标为:(,)
由图象可知:2,
∵a>0,
∴4ac﹣b2<﹣8a,
即b2﹣4ac>8a,故③错误;
④由图象可知:1,a>0,
∴2a+b<0,
∵9a+3b+c=0,
∴c=﹣9a﹣3b,
∴5a+b+c=5a+b﹣9a﹣3b=﹣4a﹣2b=﹣2(2a+b)>0,故④正确;
故选:C.
5.已知、和都是非零向量,在下列选项中,不能判定的是( )
A., B.||=|| C. D.,
【解答】解:A、∵,,∴,故本选项错误;
B、∵||=||,∴与的模相等,但不一定平行,故本选项正确;
C、∵,∴,故本选项错误;
D、∵,,∴,故本选项错误.
故选:B.
6.在△ABC中,E、F是BC边上的三等分点,BM是AC边上的中线,AE、AF分BM为三段的长分别是x、y、z,若这三段有x>y>z,则x:y:z等于( )
A.3:2:1 B.4:2:1 C.5:2:1 D.5:3:2
【解答】解:如图,作MH∥BC交AE于H,交AF于G,设AE交BM于K,AF交BM于J.
∵MH∥BC,
∴,
∵BE=EF=CF,
∴HG=MGCF,
∴,
∴y+z=x,
∴,
∴x+y=4z,
∴xz,yz,
∴x:y:z=5:3:2,
故选:D.
二.填空题(共12小题,满分48分,每小题4分)
7.已知2x=5y,那么 .
【解答】解:∵2x=5y,
∴设x=5a,则y=2a,
那么.
故答案为:.
8.计算:3(2)﹣2(3)= .
【解答】解:3(2)﹣2(3)
=3323
=(3﹣2)(﹣3+3)
.
故答案是:.
9.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 ﹣1 .
【解答】解:∵二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,
∴a2﹣1=0,
∴a=±1,
∵a﹣1≠0,
∴a≠1,
∴a的值为﹣1.
故答案为:﹣1.
10.抛物线y=2x2﹣4x﹣3,当﹣1≤x≤4时,y的取值范围是 ﹣5≤y≤13 .
【解答】解:∵y=2x2﹣4x﹣3
=2(x2﹣2x)﹣3,
=2(x2﹣2x+1﹣1)﹣3,
=2(x﹣1)2﹣5,
∴当x=1时,y最小值=﹣5,
∵﹣1≤x≤4,且|4﹣1>|﹣1﹣1|,
∴x=4时,y最大=13,
∴当﹣1≤x≤4时,y的取值范围是:﹣5≤y≤13.
故答案为﹣5≤y≤13.
11.如图,E、F是线段AB的两个黄金分割点,AB=1,则线段EF的长为 2 .(结果保留根号)
【解答】解:∵E、F是线段AB的两个黄金分割点,
∴AF=BEAB,
∴EF=AF+BE﹣AB2,
故答案为:2.
12.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 15 .
【解答】解:∵AB∥CD,
∴△ABE∽△DCE,
∴,
∴,
∵EF∥CD,
∴△BEF∽△BCD,
∴,
∵EF=6,
∴CD=15,
故答案为15.
13.当两个相似三角形的相似比为 1: 时,这两个相似三角形的面积比是1:2.
【解答】解:∵相似三角形的面积比等于相似比的平方,
∴两个相似三角形的面积比是1:2时,两个相似三角形的相似比为:1:.
故答案为:1:.
14.在Rt△ABC中,∠ACB=90°,若tanA=3,AB,则BC= 3
【解答】解:∵在Rt△ABC中,tanA3,
∴设BC=3x,则AC=x,
由BC2+AC2=AB2可得9x2+x2=10,
解得:x=1(负值舍去),
则BC=3,
故答案为:3.
15.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 1.02 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解答】解:由题意可得:
∵∠ABO=70°,AB=6m,
∴sin70°0.94,
解得:AO=5.64(m),
∵∠CDO=50°,DC=6m,
∴sin50°0.77,
解得:CO=4.62(m),
则AC=5.64﹣4.62=1.02(m),
答:AC的长度约为1.02米.
故答案为:1.02.
16.如图,已知∠BAC=∠DAE,请你再补充一个条件 ∠B=∠D等 ,使得△ABC∽△ADE.
【解答】解:∵∠BAC=∠DAE,
∠B=∠D,
∴△ABC∽△ADE,
故答案为:∠B=∠D等
17.如图,在△ABC中,∠ACB=90°,AC=BC=6,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为 5 .
【解答】解:如图,将△CBN顺时针旋转90度,得到△ACR,连接RM
则△CRA≌△CNB全等,
∴AR=BN,∠B=∠CAR,∠BCN=∠ACR,
∵∠ACB=90°,AC=BC=6,
∴AB=12,∠B=∠CAB=45°,
∴∠CAR=45°,
∴∠MAR=90°,
∵∠MCN=45°,
∴∠BCN+∠ACM=45°=∠ACM+∠ACR,
∴∠MCN=∠MCR,且CN=CR,CM=CM,
∴△CNM≌△CRM(SAS)
∴MN=MR,
∵AB=12,AM=3,
∴BN+MN=9,
∴BN=AR=9﹣MN,
∵MR2=AM2+AR2,
∴MN2=(9﹣MN)2+9,
∴MN=5
故答案为5.
18.如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△ABD,AB与边BC交于点E.若△DEB′为直角三角形,则BD的长是 1或 .
【解答】解:(1)当∠EDB′=90°时,如图1所示:
由折叠得:∠B=∠B′,BD=B′D,
在Rt△ABC中,AB5,
∵∠AEC=∠DEB′,∠C=∠EDB′=90°,
∴∠B=∠B′=∠CAE,
∴△ACE∽△BCA,
∴,即:,
∴CE,AE,
∴BE=5,
设BD=x=B′D,则DE=4xx,
在Rt△DEB′中,由勾股定理得:
()2=x2+(x)2,
解得:x1=1,x21(舍去),
(2)当∠DEB′=90°时,此时点E与点C重合,如图2所示:
由折叠得,AB=AB′=5,
∴EB′=5﹣3=2,设BD=x,则B′D=x,ED=4﹣x
在Rt△DEB′中,由勾股定理得:
x2=22+(4﹣x)2,解得:x,
故答案为:1或.
三.解答题(共7小题,满分78分)
19.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
【解答】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴,解得,
∴所求的抛物线的函数表达式为y=﹣x2+2x+3;
(2)如图,连接PC,PE.
抛物线的对称轴为x1.
当x=1时,y=4,
∴点D的坐标为(1,4).
设直线BD的解析式为y=kx+b,
则,
解得.
∴直线BD的解析式为:y=﹣2x+6,
设点P的坐标为(x,﹣2x+6),又C(0,3),E(1,0),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,
∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,
解得,x=2,
则y=﹣2×2+6=2,
∴点P的坐标为(2,2).
20.如图,在?ABCD中,点E是BC边的中点,设,.
(1)试用向量,表示向量,则 . ;
(2)在图中求作:、.(保留作图痕迹,不要求写作法,但要写出结果)
【解答】解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是BC的中点,
∴BE=EC,
∵,,,
∴.
故答案为:.
(2)如图,,.
向量,向量即为所求.
21.已知:如图,在△ABC中,D是边AB上一点,AC2=AD?AB,AE⊥CD,垂足为点E,AD=4,AC=2,且∠ACB=60°.
(1)求AE的长;
(2)求sin∠DCB的值.
【解答】解:(1)∵AC2=AD?AB,∴,
∵∠DAC∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB=60°,∠ACD=∠ABC,
∵∠AED=90°,AD=4,
∴DE=2,
∴AE2;
(2)∵,AC2=AD?AB,
∴AB,
∴EC2,
∴∠ACD=45°,
∴∠ABC=∠ACD=45°,
过点D作DF⊥BC,垂足为F,
∴BF=DF=2,
∵DC=DE+CE=2+2,
∴sin∠DCB.
22.如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
【解答】解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,
在Rt△BFD中,sin∠DBF,
则DF=BD?sin∠DBF≈6×0.54=3.24,
cos∠DBF,
则BF=BD?cos∠DBF≈6×0.84=5.04,
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=5.04,CF=BE=CD﹣DF=4﹣3.24=0.76,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=5.04,
∴AB=AE+BE=5.04+0.76=5.8,
答:建筑物AB的高约为5.8m.
23.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE=∠C,∠DAE=∠BAD,
∴∠ADE=∠B,
∴∠AED=∠ADB.
∵∠BED+∠AED=∠CDA+∠ADB=180°,
∴∠BED=∠CDA,
∴△BDE∽△CAD.
(2)解∵AB=AC=5,BC=8,CD=2,
∴BD=6.
∵△BDE∽△CAD,
∴,即,
∴BE.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
【解答】解:(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,
PF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APCAQ?PFx2x+3(x)2.
∵0,
∴当x时,△APC的面积取最大值,最大值为,此时点P的坐标为(,).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC3,AN,
∴C△ANM=AM+MN+AN=AC+AN=3.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
25.如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.
(1)若a=12.
①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为 3 ;
②在运动过程中,求四边形AMQP的最大面积;
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.
【解答】(1)解:①P在线段AD上,PQ=AB=20,AP=x,AM=12,
四边形AMQP的面积(12+20)x=48,
解得:x=3;
故答案为:3;
②当P,在AD上运动时,P到D点时四边形AMQP面积最大,为直角梯形,
∴0<x≤10时,四边形AMQP面积的最大值(12+20)10=160,
当P在DG上运动,10<x<20,四边形AMQP为不规则梯形,
作PK⊥AB于K,交CD于N,作GE⊥CD于E,交AB于F,如图2所示:
则PK=x,PN=x﹣10,EF=BC=10,
∵△GDC是等腰直角三角形,
∴DE=CE,GECD=10,
∴GF=GE+EF=20,
∴GH=20﹣x,
由题意得:PQ∥CD,
∴△GPQ∽△GDC,
∴,
即,
解得:PQ=40﹣2x,
∴梯形AMQP的面积(12+40﹣2x)×x=﹣x2+26x=﹣(x﹣13)2+169,
∴当x=13时,四边形AMQP的面积最大=169;
(2)解:P在DG上,则10≤x<20,AM=a,PQ=40﹣2x,
梯形AMQP的面积S(a+40﹣2x)×x=﹣x2x,对称轴为:x=10,
∵0≤a≤20,
∴10≤1015,对称轴在10和15之间,
∵10≤x<20,二次函数图象开口向下,
∴当x无限接近于20时,S最小,
∴﹣20220≥50,
∴a≥5;
综上所述,a的取值范围为5≤a≤20.
(
1
)
同课章节目录
