人教版九年级下册数学第二十八章:28.2.1 解直角三角形 课件 (共19张PPT)
文档属性
| 名称 | 人教版九年级下册数学第二十八章:28.2.1 解直角三角形 课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 694.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-17 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
【人教版 数学 九年(下)第28章 锐角三角函数】
A
B
C
“斜而未倒”
意大利的伟大科学家伽俐·略,曾在斜塔的顶层做过自由落体运动的实验 .
情境引入
你能求出∠A的度数吗?
如图所示,已知在Rt△ABC中,∠C=90°,BC=5.2 m,
AB=54.5 m.
利用计算器可得
∠A≈50°28′
直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
回顾旧知
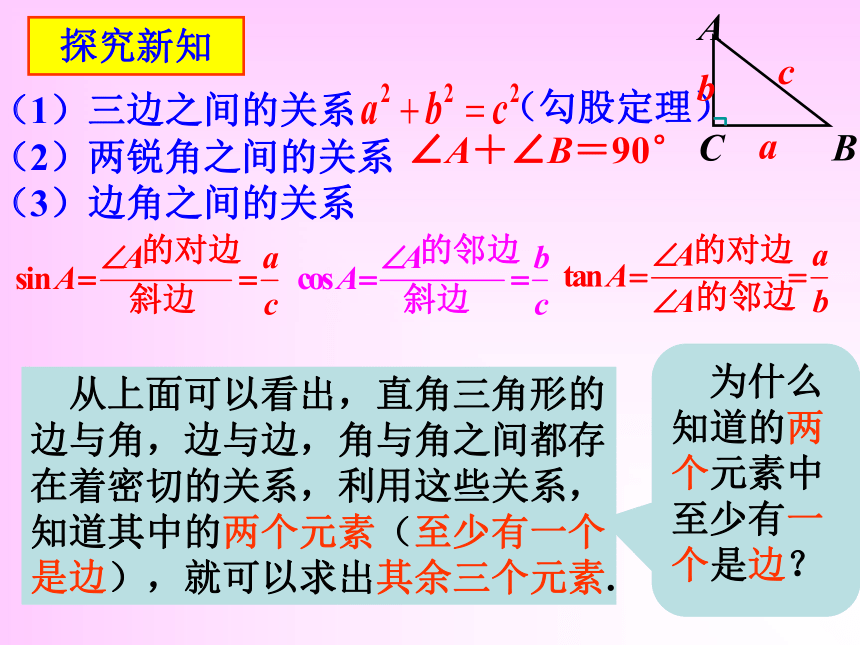
在Rt△ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
回顾旧知
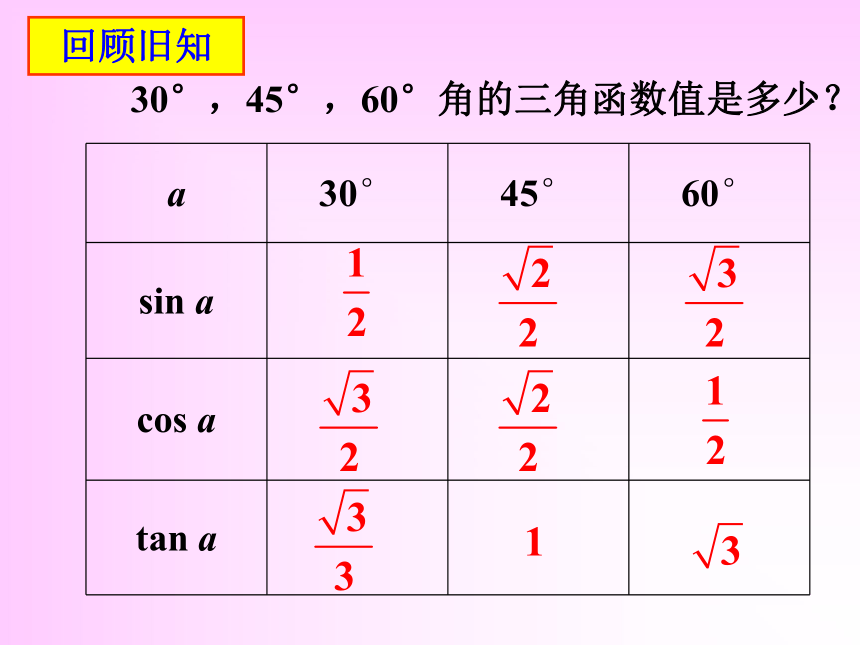
30°,45°,60°角的三角函数值是多少?
a 30° 45° 60°
sin a
cos a
tan a
探究新知
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
从上面可以看出,直角三角形的边与角,边与边,角与角之间都存在着密切的关系,利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个元素.
为什么知道的两个元素中至少有一个是边?
的邻边
探究新知
解:
例1:如图所示,在Rt△ABC中,∠C=90°,AC = ,BC= ,解这个直角三角形.
已知两直角边,如何解这个直角三角形?
探究新知
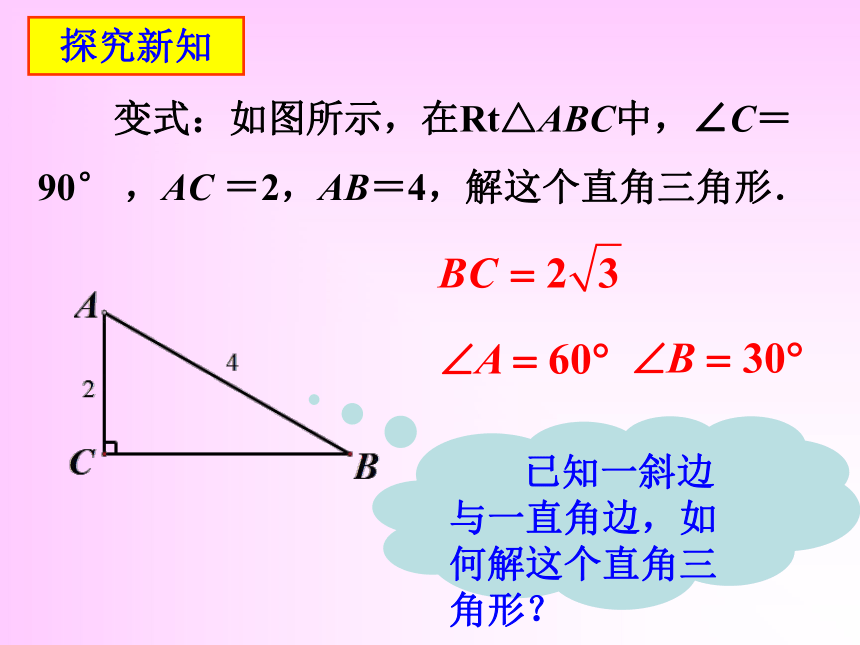
已知一斜边与一直角边,如何解这个直角三角形?
变式:如图所示,在Rt△ABC中,∠C=90° ,AC =2,AB=4,解这个直角三角形.
探究新知
归纳1:已知两边:
1. 求第三边(勾股定理)
2. 求角(根据锐角三角函数)
探究新知
解:∠A=90°-∠B=90°-35°=55°
你还有其他方法求出c吗?
例2:如图所示,在Rt△ABC中,∠C=900,∠B=35°,b=20,解这个直角三角形.(结果保留小数点后一位)
已知一直角边与一锐角,如何解这个直角三角形?
探究新知
已知一斜边与一锐角,如何解这个直角三角形?
变式:如图所示,在Rt△ABC中,∠C=90°,∠B=30°,c=30,解这个直角三角形.
探究新知
归纳2:已知一锐角、一边(直角边或斜边):
1. 求另一角(根据∠A+∠B=90°)
2. 求其它边(根据锐角三角函数)
巩固提高
1. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)c=30,b=20;
(2)∠B=72°,c=14;
(3)∠B=30°,a= .
巩固提高
2.?在Rt△ABC中,∠C为直角,AC=6,∠BAC的平分线AD= ,解此直角三角形.
巩固提高
3. 如图,在△ABC中,AB=5,AC=7,∠B=60°.求BC的长.
解:过点A作AD⊥BC于D.
体验收获
说一说你的收获 ……
1. 解直角三角形的概念
2. 解直角三角形的方法
3. 解决问题要结合图形
拓展提升
在Rt△ABC中,∠C=90°.
(1)已知∠A,c,写出解Rt△ABC的过程;
(2)已知∠A,a,写出解Rt△ABC的过程;
(3)已知a,c,写出解Rt△ABC 的过程.
解:
(1)
(2)
(3)
由 求出∠A,
课内检测
在Rt△ABC中,∠C=90°根据下列条件解直角三角形:
(1)c=20,∠A=45°;
(2)a=36,∠B=30°;
(3)a=19, c= ;
(4)
布置作业
必做题:
选做题:
教材77页习题28.2第1、2题
在Rt△ABC中,∠C=90°, ,∠B的平分线BD=16,求AB.
【人教版 数学 九年(下)第28章 锐角三角函数】
A
B
C
“斜而未倒”
意大利的伟大科学家伽俐·略,曾在斜塔的顶层做过自由落体运动的实验 .
情境引入
你能求出∠A的度数吗?
如图所示,已知在Rt△ABC中,∠C=90°,BC=5.2 m,
AB=54.5 m.
利用计算器可得
∠A≈50°28′
直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
回顾旧知
在Rt△ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
回顾旧知
30°,45°,60°角的三角函数值是多少?
a 30° 45° 60°
sin a
cos a
tan a
探究新知
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
从上面可以看出,直角三角形的边与角,边与边,角与角之间都存在着密切的关系,利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个元素.
为什么知道的两个元素中至少有一个是边?
的邻边
探究新知
解:
例1:如图所示,在Rt△ABC中,∠C=90°,AC = ,BC= ,解这个直角三角形.
已知两直角边,如何解这个直角三角形?
探究新知
已知一斜边与一直角边,如何解这个直角三角形?
变式:如图所示,在Rt△ABC中,∠C=90° ,AC =2,AB=4,解这个直角三角形.
探究新知
归纳1:已知两边:
1. 求第三边(勾股定理)
2. 求角(根据锐角三角函数)
探究新知
解:∠A=90°-∠B=90°-35°=55°
你还有其他方法求出c吗?
例2:如图所示,在Rt△ABC中,∠C=900,∠B=35°,b=20,解这个直角三角形.(结果保留小数点后一位)
已知一直角边与一锐角,如何解这个直角三角形?
探究新知
已知一斜边与一锐角,如何解这个直角三角形?
变式:如图所示,在Rt△ABC中,∠C=90°,∠B=30°,c=30,解这个直角三角形.
探究新知
归纳2:已知一锐角、一边(直角边或斜边):
1. 求另一角(根据∠A+∠B=90°)
2. 求其它边(根据锐角三角函数)
巩固提高
1. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)c=30,b=20;
(2)∠B=72°,c=14;
(3)∠B=30°,a= .
巩固提高
2.?在Rt△ABC中,∠C为直角,AC=6,∠BAC的平分线AD= ,解此直角三角形.
巩固提高
3. 如图,在△ABC中,AB=5,AC=7,∠B=60°.求BC的长.
解:过点A作AD⊥BC于D.
体验收获
说一说你的收获 ……
1. 解直角三角形的概念
2. 解直角三角形的方法
3. 解决问题要结合图形
拓展提升
在Rt△ABC中,∠C=90°.
(1)已知∠A,c,写出解Rt△ABC的过程;
(2)已知∠A,a,写出解Rt△ABC的过程;
(3)已知a,c,写出解Rt△ABC 的过程.
解:
(1)
(2)
(3)
由 求出∠A,
课内检测
在Rt△ABC中,∠C=90°根据下列条件解直角三角形:
(1)c=20,∠A=45°;
(2)a=36,∠B=30°;
(3)a=19, c= ;
(4)
布置作业
必做题:
选做题:
教材77页习题28.2第1、2题
在Rt△ABC中,∠C=90°, ,∠B的平分线BD=16,求AB.
