人教版高中物理必修3-4讲义资料,复习补习资料:12波的传播的多解性(提高)
文档属性
| 名称 | 人教版高中物理必修3-4讲义资料,复习补习资料:12波的传播的多解性(提高) |
|
|
| 格式 | zip | ||
| 文件大小 | 359.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-16 20:19:31 | ||
图片预览



文档简介
波的传播的多解性
【学习目标】
1.理解波传播的时间周期性特征。
2.理解波传播的空间周期性特征。
【巩固练习】
一、选择题
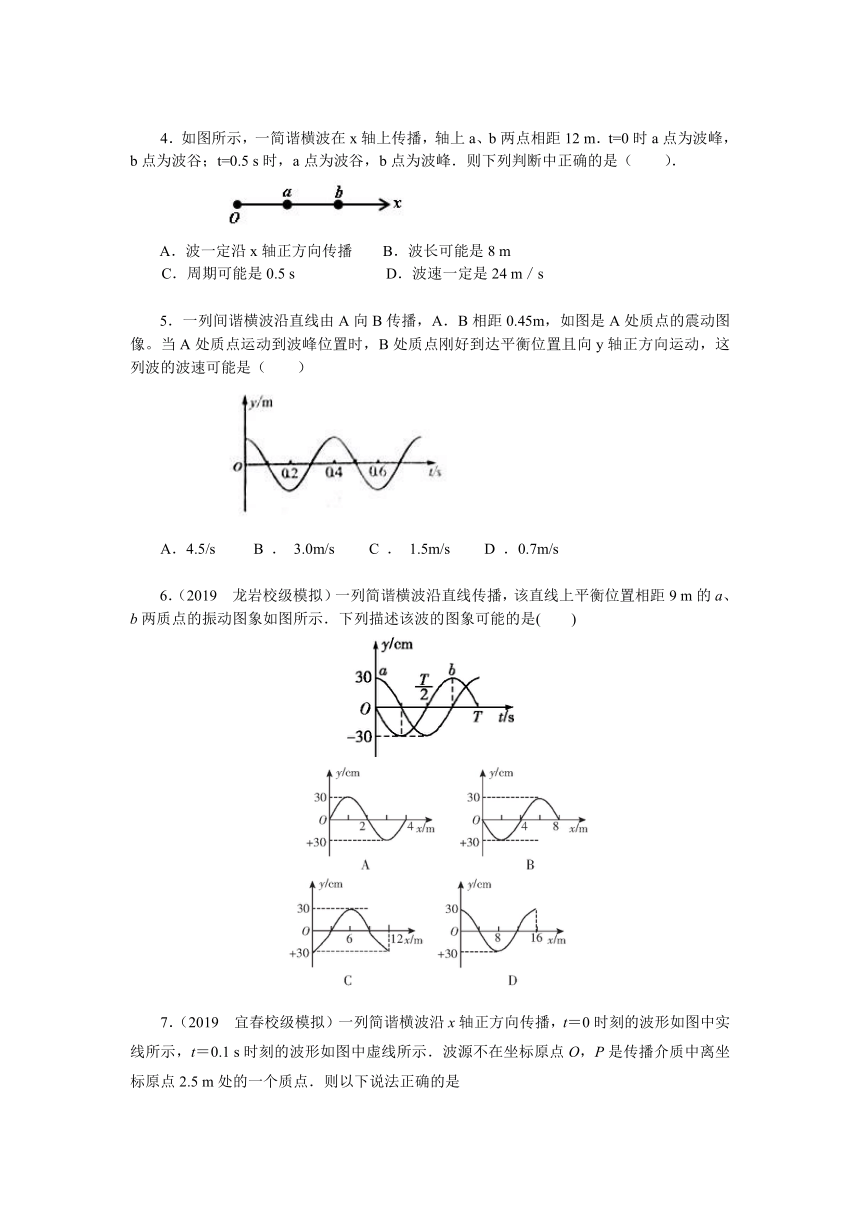
1.一列横波以10 m/s的速率沿水平方向传播.某时刻的波形如图中的实线所示,经时间Δt后的波形如图12-3-37中的虚线所示.已知2T>Δt>T(T为这列波的周期).由此可知Δt可能是( ).
A.0.3 s B.0.5 s C.0.6 s D.0.7 s
2.一列横波在t=0时刻的波形如图12-3-38中实线所示,在t=1 s时的波形如图12-3-38中虚线所示.由此可以判定此波的( ).
A.波长一定是4 cm B.周期一定是4 s
C.振幅一定是2 cm D.传播速度一定是1 cm/s
3.一简谐横波在图中x轴上传播,实线和虚线分别是t1和t2时刻的波形图,已知t2-t1=1.0 s.由图判断下列哪一个波速是不可能的?( )
A.1 m/s B.3 m/s C.5 m/s D.10 m/s
4.如图所示,一简谐横波在x轴上传播,轴上a、b两点相距12 m.t=0时a点为波峰,b点为波谷;t=0.5 s时,a点为波谷,b点为波峰.则下列判断中正确的是( ).
A.波一定沿x轴正方向传播 B.波长可能是8 m
C.周期可能是0.5 s D.波速一定是24 m/s
5.一列间谐横波沿直线由A向B传播,A.B相距0.45m,如图是A处质点的震动图像。当A处质点运动到波峰位置时,B处质点刚好到达平衡位置且向y轴正方向运动,这列波的波速可能是( )
A.4.5/s???????? B . 3.0m/s??????? C . 1.5m/s??????? D .0.7m/s
6.(2019 龙岩校级模拟)一列简谐横波沿直线传播,该直线上平衡位置相距9 m的a、b两质点的振动图象如图所示.下列描述该波的图象可能的是( )
7.(2019 宜春校级模拟)一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1 s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点2.5 m处的一个质点.则以下说法正确的是 ( )
A.波的频率可能为7.5 Hz
B.波的传播速度可能为50 m/s
C.质点P的振幅为0.1 m
D.在t=0.1 s时刻与P相距5 m处的质点也一定向上振动
?
8.一列简谐横波沿x轴传播,周期为T,t=0时刻的波形如图所示。此时平衡位置位于x=3 m处的质点正在向上运动,若a、b两质点平衡位置的坐标分别为xa=2.5 m, xb=5.5 m,则( )
A.当a质点处在波峰时,b质点恰在波谷
B.t=T/4时,a质点正在向y轴负方向运动
C.t=3T/4时,b质点正在向y轴负方向运动
D.在某一时刻,a、b两质点的位移和速度可能相同
二、填空题
9.有四列简谐波同时沿x轴正方向传播,波速分别是v,2v,3v和4v,a、b是x轴上所给定的两点,且ab=L,在t时刻a、b两点间四列波的波形分别如图所示,则由该时刻起a点出现波峰的先后顺序依次是________;频率由高到低的先后顺序依次是________。
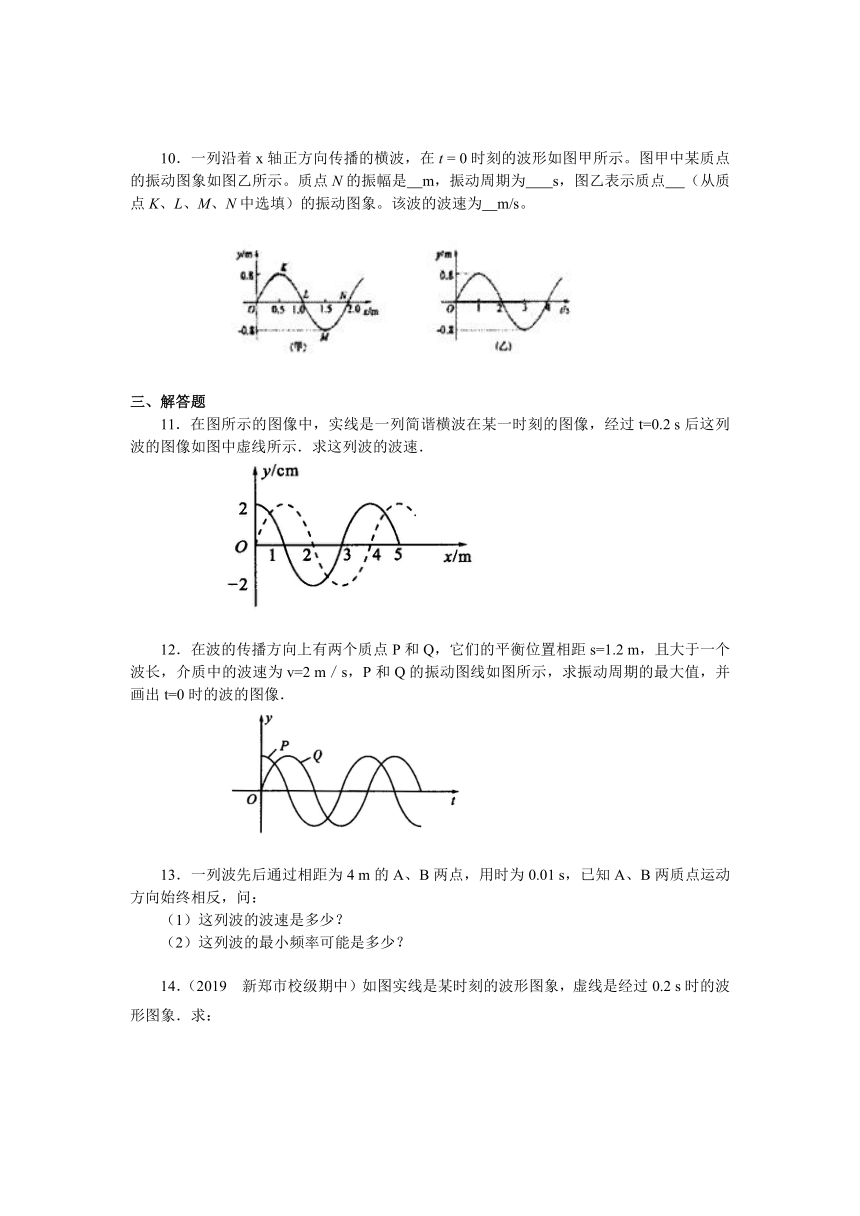
10.一列沿着x轴正方向传播的横波,在t = 0时刻的波形如图甲所示。图甲中某质点的振动图象如图乙所示。质点N的振幅是?? m,振动周期为????? s,图乙表示质点??? (从质点K、L、M、N中选填)的振动图象。该波的波速为?? m/s。
三、解答题
11.在图所示的图像中,实线是一列简谐横波在某一时刻的图像,经过t=0.2 s后这列波的图像如图中虚线所示.求这列波的波速.
12.在波的传播方向上有两个质点P和Q,它们的平衡位置相距s=1.2 m,且大于一个波长,介质中的波速为v=2 m/s,P和Q的振动图线如图所示,求振动周期的最大值,并画出t=0时的波的图像.
13.一列波先后通过相距为4 m的A、B两点,用时为0.01 s,已知A、B两质点运动方向始终相反,问:
(1)这列波的波速是多少?
(2)这列波的最小频率可能是多少?
14.(2019 新郑市校级期中)如图实线是某时刻的波形图象,虚线是经过0.2 s时的波形图象.求:
(1)波传播的可能距离;
(2)可能的周期;
(3)若波速是35 m/s,波的传播方向;
(4)若0.2 s小于一个周期时,传播的距离、周期、波速.
【答案与解析】
一、选择题
1.【答案】B、D
【解析】根据T=/v,则T=0.4 s.根据题意可知.当此波向右传播时,当此波向左传播时.
2.【答案】A、C
【解析】解波动图像的题目,一般可分为两类:一类是读图,可以直接从图上读出振幅和波长,此题便可读出波长是4 cm,振幅是2 cm,故A、C选项正确.另一类是根据图像给定的条件,去计算波速、周期,判定波传播的方向,判定某一质点的运动情况及判定某一时刻的波形图.这类问题的解决,是建立在正确读图和对波动的正确理解上的,是较深层次的考查.此题表示出在1 s时间内图像的变化.这1 s时间与周期的关系是(n=0,1,2,3,…),是不确定解,因此B选项错.同理传播速度也不确定,D选项也错.
3.【答案】D
【解析】由图知此简谐横波的波长为4 m.设简谐横波向右传播,
(n=0,1,2,3,…),则v可能为1 m/s,5 m/s,9 m/s,…
设简谐横波向左传播,(n=0,1,2,3,…),v'可能为3 m/s,7 m/s,11 m/s,…
所以选项A、B、C都是可能的,D选项不可能.
4.【答案】B
【解析】由于x=-0时a点为波峰,b点为波谷,所以a、b两点的间距为半波长的奇数倍.
则有12m=(2n+1)(n=0,1,2,3,…),
所以(n=0,1,2,3,…).
当n=1时,=8 m,故B正确.
由于经t=0.5 s,a点为波谷,b点为波峰,所以0.5 s为半个周期的奇数倍,则有0.5 s=(2m+1)(m=0,1,2,3,…),
所以(m=0,1,2,3,…)。
设T=0.5 s,则,所以周期不可能为0.5 s,故C错.
由于机械波具有双向性和周期性,所以A、D均错.
5.【答案】A
?
【解析】在处理相距一定距离的两个质点关系时必须尝试作出两质点间在该时刻的最少波形,然后根据间距和波长关系求波长(注意波的周期性)。波是由A向B传播的,而且在A到达波峰的时刻,处于B平衡位置向上运动,则最少波形关系如图,所以有,,,当n=0时,v=4.5m/s,当n=1时v=0.9m/s,当n=2时v=0.5m/s等,正确答案为A。
6.【答案】AC
【解析】由振动图象可知,t=0时,a在正的最大位移处,b在平衡位置向y轴负方向运动.如果波从a传播到b,则ab间距最短应该为波长的情况,则 (其中n=0,1,2…),波长可能为12 m、、…,故选项C正确;如果波从b传播到a,则ab间距最短应该为波长的情况, (其中n=0,1,2…),波长可能为36 m、 、4 m、…,故选项A正确.
7.【答案】BC
【解析】从题图中可以看出波形从实线传播到虚线的时间为: (n=0,1,2,…),波的频率为:(n=0,1,2,…),A错误;从题图中得出波长为:λ=4 m,波的传播速度为:v=λf=10(4n+1) m/s(n=0,1,2,…),当n=1时,v=50 m/s,B正确;从题图中可以看出质点P的振幅为0.1 m,C正确;从题图中可知t=0.1 s时,质点P向上振动,与P相距5 m的质点与质点P相距个波长,若该质点在P点左侧,它正在向下振动,若该质点在P点右侧,它正在向上振动,D错误.
8.【答案】见解析
【解析】由题图知,波长λ=4m,a、b两质点的平衡位置相距为Δx=5.5m-2.5m=3m,比较Δx和λ,Δx既不是λ/2的奇数倍,亦不是偶数倍,即,a、b两点既不是同相点亦不是反相点,故,A、D都错。
由t=0时平衡位置位于x=3 m处的质点正在向上运动,知波沿x轴负方向传播。据此可作出T/4.3T/4时刻的波形如5图中的粗虚线、细虚线所示,可看出,T/4时a质点正向y轴正方向运动,3T/4时b质点正向y轴负方向运动。故,B错C对,故本题选C。
二、填空题
9.【答案】B、D、C、A D、B、C、A
【解析】根据已给的波动图像,可得出四列简谐波的波长,周期(频率)关系为:
A=L,TA=A/vA=L/v,fA=v/L.
B=L/2,TB=L/4v,fB=4v/L.
C=2L,TC=2L/3v,fC=3v/2L.
D=2L/3,TD=L/6v,fD=6v/L.
易得频率关系fD>fB>fC>fA.再根据波动图像得出A、B、C选项中,t时刻质点a向上振动,D选项中,在t时刻,质点a向下振动,所以从该时刻起质点a第一次达到波峰的时间分别为:
tA=TA/4=L/4v,fB=TB/4=L/16v,
tC=TC/4=L/6v,tD=3TD/4=L/8v,
得tB<tD<tC<tA.
10.【答案】见解析
【解析】由波动(或振动)图像可看出,质点N的振幅是0.8m,该波的波长是2.0m。振动中各质点的周期相同,由振动图像可知,各质点的振动周期为4s。由振动图像可知,该质点0时刻,过平衡位置向y轴正方向运动,结合波动图像可以看出图乙表示的是质点N的振动图像。由v=λ/T可解得:v=0.5m/s。
三、解答题
11.【答案】见解析
【解析】从波的图像可读出波长=4 m,振幅A=2 cm.此题引起多种可能的原因有两个,一个是传播方向的不确定,一个是时间t和周期T的大小关系不确定.
设波沿x轴正方向传播,t=0.2 s可能是个周期(n=0,1,2,3,…),即,周期,波速m/s(n=0,1,2,3,…).
设波沿x轴负方向传播,t=0.2 s可能是个周期(n=0,1,2,3,…),即,周期,波速(n=0,1,2,3,…).
即当波沿x轴正方向传播时,v=5(4n+1)m/s(n=0,1,2,3…),当波沿x轴负方向传播时,v=5(4n+3) m/s(n=0,1,2,3,…).
12.【答案】见解析
【解析】这是一道波动与振动图像相结合的问题,通过振动图像确定每一时刻质点的振动方向,然后由P、Q两点振动情况,确定两者间距与波长的关系;又因为波的传播方向未知,可从下面两种情况加以分析:
(1)当波由P点向Q点传播
由振动图线可知Q点的振动在时间上比P点至少落后,因而P、Q两点之间的距离至少是,根据波的周期性,s与关系应为(注意题目中s>)s=n+(n=1,2,3,…),,故周期(n=1,2,3,…),显然,n=1时,和T有最大值,其最大值分剐为1=0.96 m,T1=0.48 s.
下面作出t=0时的波的图像,要正确画出该时刻波的图线,需把握好以下几点:
①根据题中振动图像,t=0时P点位移yP=A,速度vP=0;Q点位移yQ=0,速度最大,且将向正最大位移振动.
②以P点为原点,pQ为x轴画出直角坐标系,并根据及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出。然后画出经过这两点的一条图线,如图(a)所示.
(2)当波由Q点向P点传播
这种情况下与(1)的求解方法基本相同.
所以(n=1,2,3,…),,(n=1,2,3,…).
当n=1时,和T取最大值,其最大值分别为,,t=0时波的图像如图(b)所示.
13.【答案】见解析
【解析】(1).
(2)A、B两质点的振动方向始终相反,即属于振动步调始终相反的点,因此两点平衡位置间的距离s=4 m=+n=.所以(n=0,1,2,…),即由v=f可得(n=0,1,2,…),
则当n=0时有最小频率f=50 Hz.
14.【答案】见解析
【解析】(1)由题图知,波长λ=4 m,
沿x轴向左传播时,传播的距离为
(n=0,1,2…)
沿x轴向右传播时,传播的距离为
(n=0,1,2…)
(2)向左传播时,传播的时间为得
(n=0,1,2…)
向右传播时,传播的时间为得
(n=0,1,2…)
(3)若波速是35 m/s,则波在0.2 s内传播的距离为
,所以波向左传播.
(4)若0.2 s小于一个周期,说明波在0.2 s内传播的距离小于一个波长.
向左传播时,传播的距离;
由传播的时间得周期T≈0.267 s,波速v≈15 m/s.
向右传播时,传播的距离为;
由传播的时间得周期T=0.8 s,波速v=5 m/s.
【学习目标】
1.理解波传播的时间周期性特征。
2.理解波传播的空间周期性特征。
【巩固练习】
一、选择题
1.一列横波以10 m/s的速率沿水平方向传播.某时刻的波形如图中的实线所示,经时间Δt后的波形如图12-3-37中的虚线所示.已知2T>Δt>T(T为这列波的周期).由此可知Δt可能是( ).
A.0.3 s B.0.5 s C.0.6 s D.0.7 s
2.一列横波在t=0时刻的波形如图12-3-38中实线所示,在t=1 s时的波形如图12-3-38中虚线所示.由此可以判定此波的( ).
A.波长一定是4 cm B.周期一定是4 s
C.振幅一定是2 cm D.传播速度一定是1 cm/s
3.一简谐横波在图中x轴上传播,实线和虚线分别是t1和t2时刻的波形图,已知t2-t1=1.0 s.由图判断下列哪一个波速是不可能的?( )
A.1 m/s B.3 m/s C.5 m/s D.10 m/s
4.如图所示,一简谐横波在x轴上传播,轴上a、b两点相距12 m.t=0时a点为波峰,b点为波谷;t=0.5 s时,a点为波谷,b点为波峰.则下列判断中正确的是( ).
A.波一定沿x轴正方向传播 B.波长可能是8 m
C.周期可能是0.5 s D.波速一定是24 m/s
5.一列间谐横波沿直线由A向B传播,A.B相距0.45m,如图是A处质点的震动图像。当A处质点运动到波峰位置时,B处质点刚好到达平衡位置且向y轴正方向运动,这列波的波速可能是( )
A.4.5/s???????? B . 3.0m/s??????? C . 1.5m/s??????? D .0.7m/s
6.(2019 龙岩校级模拟)一列简谐横波沿直线传播,该直线上平衡位置相距9 m的a、b两质点的振动图象如图所示.下列描述该波的图象可能的是( )
7.(2019 宜春校级模拟)一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1 s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点2.5 m处的一个质点.则以下说法正确的是 ( )
A.波的频率可能为7.5 Hz
B.波的传播速度可能为50 m/s
C.质点P的振幅为0.1 m
D.在t=0.1 s时刻与P相距5 m处的质点也一定向上振动
?
8.一列简谐横波沿x轴传播,周期为T,t=0时刻的波形如图所示。此时平衡位置位于x=3 m处的质点正在向上运动,若a、b两质点平衡位置的坐标分别为xa=2.5 m, xb=5.5 m,则( )
A.当a质点处在波峰时,b质点恰在波谷
B.t=T/4时,a质点正在向y轴负方向运动
C.t=3T/4时,b质点正在向y轴负方向运动
D.在某一时刻,a、b两质点的位移和速度可能相同
二、填空题
9.有四列简谐波同时沿x轴正方向传播,波速分别是v,2v,3v和4v,a、b是x轴上所给定的两点,且ab=L,在t时刻a、b两点间四列波的波形分别如图所示,则由该时刻起a点出现波峰的先后顺序依次是________;频率由高到低的先后顺序依次是________。
10.一列沿着x轴正方向传播的横波,在t = 0时刻的波形如图甲所示。图甲中某质点的振动图象如图乙所示。质点N的振幅是?? m,振动周期为????? s,图乙表示质点??? (从质点K、L、M、N中选填)的振动图象。该波的波速为?? m/s。
三、解答题
11.在图所示的图像中,实线是一列简谐横波在某一时刻的图像,经过t=0.2 s后这列波的图像如图中虚线所示.求这列波的波速.
12.在波的传播方向上有两个质点P和Q,它们的平衡位置相距s=1.2 m,且大于一个波长,介质中的波速为v=2 m/s,P和Q的振动图线如图所示,求振动周期的最大值,并画出t=0时的波的图像.
13.一列波先后通过相距为4 m的A、B两点,用时为0.01 s,已知A、B两质点运动方向始终相反,问:
(1)这列波的波速是多少?
(2)这列波的最小频率可能是多少?
14.(2019 新郑市校级期中)如图实线是某时刻的波形图象,虚线是经过0.2 s时的波形图象.求:
(1)波传播的可能距离;
(2)可能的周期;
(3)若波速是35 m/s,波的传播方向;
(4)若0.2 s小于一个周期时,传播的距离、周期、波速.
【答案与解析】
一、选择题
1.【答案】B、D
【解析】根据T=/v,则T=0.4 s.根据题意可知.当此波向右传播时,当此波向左传播时.
2.【答案】A、C
【解析】解波动图像的题目,一般可分为两类:一类是读图,可以直接从图上读出振幅和波长,此题便可读出波长是4 cm,振幅是2 cm,故A、C选项正确.另一类是根据图像给定的条件,去计算波速、周期,判定波传播的方向,判定某一质点的运动情况及判定某一时刻的波形图.这类问题的解决,是建立在正确读图和对波动的正确理解上的,是较深层次的考查.此题表示出在1 s时间内图像的变化.这1 s时间与周期的关系是(n=0,1,2,3,…),是不确定解,因此B选项错.同理传播速度也不确定,D选项也错.
3.【答案】D
【解析】由图知此简谐横波的波长为4 m.设简谐横波向右传播,
(n=0,1,2,3,…),则v可能为1 m/s,5 m/s,9 m/s,…
设简谐横波向左传播,(n=0,1,2,3,…),v'可能为3 m/s,7 m/s,11 m/s,…
所以选项A、B、C都是可能的,D选项不可能.
4.【答案】B
【解析】由于x=-0时a点为波峰,b点为波谷,所以a、b两点的间距为半波长的奇数倍.
则有12m=(2n+1)(n=0,1,2,3,…),
所以(n=0,1,2,3,…).
当n=1时,=8 m,故B正确.
由于经t=0.5 s,a点为波谷,b点为波峰,所以0.5 s为半个周期的奇数倍,则有0.5 s=(2m+1)(m=0,1,2,3,…),
所以(m=0,1,2,3,…)。
设T=0.5 s,则,所以周期不可能为0.5 s,故C错.
由于机械波具有双向性和周期性,所以A、D均错.
5.【答案】A
?
【解析】在处理相距一定距离的两个质点关系时必须尝试作出两质点间在该时刻的最少波形,然后根据间距和波长关系求波长(注意波的周期性)。波是由A向B传播的,而且在A到达波峰的时刻,处于B平衡位置向上运动,则最少波形关系如图,所以有,,,当n=0时,v=4.5m/s,当n=1时v=0.9m/s,当n=2时v=0.5m/s等,正确答案为A。
6.【答案】AC
【解析】由振动图象可知,t=0时,a在正的最大位移处,b在平衡位置向y轴负方向运动.如果波从a传播到b,则ab间距最短应该为波长的情况,则 (其中n=0,1,2…),波长可能为12 m、、…,故选项C正确;如果波从b传播到a,则ab间距最短应该为波长的情况, (其中n=0,1,2…),波长可能为36 m、 、4 m、…,故选项A正确.
7.【答案】BC
【解析】从题图中可以看出波形从实线传播到虚线的时间为: (n=0,1,2,…),波的频率为:(n=0,1,2,…),A错误;从题图中得出波长为:λ=4 m,波的传播速度为:v=λf=10(4n+1) m/s(n=0,1,2,…),当n=1时,v=50 m/s,B正确;从题图中可以看出质点P的振幅为0.1 m,C正确;从题图中可知t=0.1 s时,质点P向上振动,与P相距5 m的质点与质点P相距个波长,若该质点在P点左侧,它正在向下振动,若该质点在P点右侧,它正在向上振动,D错误.
8.【答案】见解析
【解析】由题图知,波长λ=4m,a、b两质点的平衡位置相距为Δx=5.5m-2.5m=3m,比较Δx和λ,Δx既不是λ/2的奇数倍,亦不是偶数倍,即,a、b两点既不是同相点亦不是反相点,故,A、D都错。
由t=0时平衡位置位于x=3 m处的质点正在向上运动,知波沿x轴负方向传播。据此可作出T/4.3T/4时刻的波形如5图中的粗虚线、细虚线所示,可看出,T/4时a质点正向y轴正方向运动,3T/4时b质点正向y轴负方向运动。故,B错C对,故本题选C。
二、填空题
9.【答案】B、D、C、A D、B、C、A
【解析】根据已给的波动图像,可得出四列简谐波的波长,周期(频率)关系为:
A=L,TA=A/vA=L/v,fA=v/L.
B=L/2,TB=L/4v,fB=4v/L.
C=2L,TC=2L/3v,fC=3v/2L.
D=2L/3,TD=L/6v,fD=6v/L.
易得频率关系fD>fB>fC>fA.再根据波动图像得出A、B、C选项中,t时刻质点a向上振动,D选项中,在t时刻,质点a向下振动,所以从该时刻起质点a第一次达到波峰的时间分别为:
tA=TA/4=L/4v,fB=TB/4=L/16v,
tC=TC/4=L/6v,tD=3TD/4=L/8v,
得tB<tD<tC<tA.
10.【答案】见解析
【解析】由波动(或振动)图像可看出,质点N的振幅是0.8m,该波的波长是2.0m。振动中各质点的周期相同,由振动图像可知,各质点的振动周期为4s。由振动图像可知,该质点0时刻,过平衡位置向y轴正方向运动,结合波动图像可以看出图乙表示的是质点N的振动图像。由v=λ/T可解得:v=0.5m/s。
三、解答题
11.【答案】见解析
【解析】从波的图像可读出波长=4 m,振幅A=2 cm.此题引起多种可能的原因有两个,一个是传播方向的不确定,一个是时间t和周期T的大小关系不确定.
设波沿x轴正方向传播,t=0.2 s可能是个周期(n=0,1,2,3,…),即,周期,波速m/s(n=0,1,2,3,…).
设波沿x轴负方向传播,t=0.2 s可能是个周期(n=0,1,2,3,…),即,周期,波速(n=0,1,2,3,…).
即当波沿x轴正方向传播时,v=5(4n+1)m/s(n=0,1,2,3…),当波沿x轴负方向传播时,v=5(4n+3) m/s(n=0,1,2,3,…).
12.【答案】见解析
【解析】这是一道波动与振动图像相结合的问题,通过振动图像确定每一时刻质点的振动方向,然后由P、Q两点振动情况,确定两者间距与波长的关系;又因为波的传播方向未知,可从下面两种情况加以分析:
(1)当波由P点向Q点传播
由振动图线可知Q点的振动在时间上比P点至少落后,因而P、Q两点之间的距离至少是,根据波的周期性,s与关系应为(注意题目中s>)s=n+(n=1,2,3,…),,故周期(n=1,2,3,…),显然,n=1时,和T有最大值,其最大值分剐为1=0.96 m,T1=0.48 s.
下面作出t=0时的波的图像,要正确画出该时刻波的图线,需把握好以下几点:
①根据题中振动图像,t=0时P点位移yP=A,速度vP=0;Q点位移yQ=0,速度最大,且将向正最大位移振动.
②以P点为原点,pQ为x轴画出直角坐标系,并根据及PQ=s进行合理分度,将P、Q的横、纵坐标在坐标图上标出。然后画出经过这两点的一条图线,如图(a)所示.
(2)当波由Q点向P点传播
这种情况下与(1)的求解方法基本相同.
所以(n=1,2,3,…),,(n=1,2,3,…).
当n=1时,和T取最大值,其最大值分别为,,t=0时波的图像如图(b)所示.
13.【答案】见解析
【解析】(1).
(2)A、B两质点的振动方向始终相反,即属于振动步调始终相反的点,因此两点平衡位置间的距离s=4 m=+n=.所以(n=0,1,2,…),即由v=f可得(n=0,1,2,…),
则当n=0时有最小频率f=50 Hz.
14.【答案】见解析
【解析】(1)由题图知,波长λ=4 m,
沿x轴向左传播时,传播的距离为
(n=0,1,2…)
沿x轴向右传播时,传播的距离为
(n=0,1,2…)
(2)向左传播时,传播的时间为得
(n=0,1,2…)
向右传播时,传播的时间为得
(n=0,1,2…)
(3)若波速是35 m/s,则波在0.2 s内传播的距离为
,所以波向左传播.
(4)若0.2 s小于一个周期,说明波在0.2 s内传播的距离小于一个波长.
向左传播时,传播的距离;
由传播的时间得周期T≈0.267 s,波速v≈15 m/s.
向右传播时,传播的距离为;
由传播的时间得周期T=0.8 s,波速v=5 m/s.
