六年级上册数学试题-单元测试-数学好玩 (含答案)
文档属性
| 名称 | 六年级上册数学试题-单元测试-数学好玩 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 19:53:29 | ||
图片预览



文档简介
六年级上册数学单元测试-数学好玩
一、单选题
1.
二班可能有多少人(? )
A.?16人?????????????????????????????????????????B.?36人?????????????????????????????????????????C.?40人
2.从3名女生和2名男生中选出一对乒乓球混合双打选手,有多少种不同的组队方案
A.?9种???????????????????????????????????????B.?8种???????????????????????????????????????C.?7种???????????????????????????????????????D.?6种
3.小丽和父母到影楼照全家福,站成一排,他们有(??? )种排列方法。
A.?3??????????????????????????????????????????????B.?1??????????????????????????????????????????????C.?6
4.从 中任意选两个数相加,有(??? )种不同的和。
A.?3??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?5
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.一个有四位数的密码锁,忘记了首尾两个数字,则需要试验的密码有10种。
7.从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数。
8.在一条线段上共有9个点,则这9个点可以构成38条线段。( ??)
三、填空题
9.看图填数.? ________??-? 5=________
10.有6支班级代表队参加足球赛,若采用单循环赛制,则一共要赛(?? )
A.?16场?????????????????????????????????????B.?15场?????????????????????????????????????C.?5场?????????????????????????????????????D.?30场
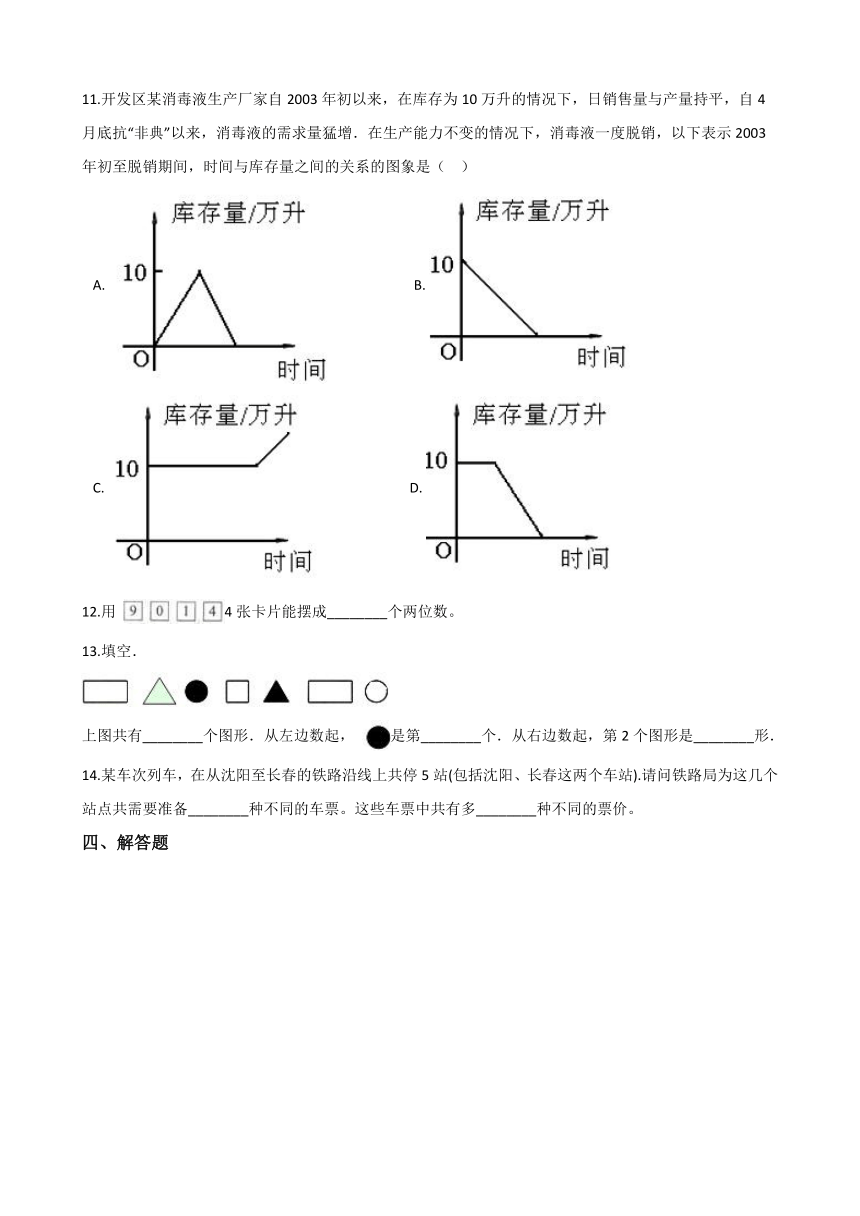
11.开发区某消毒液生产厂家自2003年初以来,在库存为10万升的情况下,日销售量与产量持平,自4月底抗“非典”以来,消毒液的需求量猛增.在生产能力不变的情况下,消毒液一度脱销,以下表示2003年初至脱销期间,时间与库存量之间的关系的图象是(?? )
A.???????????????????????B.? C.??????????????????????????D.?
12.用 4张卡片能摆成________个两位数。
13.填空. 上图共有________个图形.从左边数起, 是第________个.从右边数起,第2个图形是________形.
14.某车次列车,在从沈阳至长春的铁路沿线上共停5站(包括沈阳、长春这两个车站).请问铁路局为这几个站点共需要准备________种不同的车票。这些车票中共有多________种不同的票价。
四、解答题
15.用彩笔涂出100个方格,想一想,涂10000个方格的纸有多大?
16.3名男生,4名女生,全体排成一行,问下列情形各有多少种不同的排法: (1)甲不在中间也不在两端; (2)男、女生分别排在一起; (3)男女相间.
五、综合题
17.我发现啦!??
(1)
我发现始终是________个 ,________个 。
(2)
我发现________。
(3)50 ?48 ?46 ?44 ?42 ?40
我发现________。
(4)
我发现________。
(5)我也会照样子画一组。________。
六、应用题
18.看图列式计算
19.为迎接2008年奥运会在北京召开,我校准备举行校羽毛球单打比赛.要求每班出2~3名选手参加比赛.六年三班有4名男同学和3名女同学报名参加,若从中派3名选手组队,要求队员男女都有,有多少种组队方案?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:二班人数比一班少,但是接近,所以二班的人数可以是36人.
故答案为:B.
【分析】二班人数比一班少一些,那么二班人数就应该比一班人数38人少,且比较接近38人,再结合给出的选项即可解答.本题主要考查学生:结合答案选项以及对多一些的知识了解情况.
2.【答案】 D
【解析】【解答】解:3×2=6(种)
故答案为:D。
【分析】一名女生与一名男生组合进行混合双打时,则有2种不同的组合方法,所以用3乘2即可求出3名女生与2名男生混合打时的组队方案。
3.【答案】 C
【解析】【解答】3×2=6(种) 故答案为:C。 【分析】可以这样想:小丽在最左边,其他两人交换后,有2种排列方法,同样其他两人在最左边时,又分别有2种排列方法,照相是排列有顺序的,因此用乘法即可解答。
4.【答案】 A
【解析】【解答】解:1+2=3,1+3=4,2+3=5,共3种不同的和。 故答案为:A。 【分析】把3个数字两两相加,分别求出和即可确定和的种类。
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】错误
【解析】【解答】解:10×10=100种,因此需要试验的密码有100种,原题说法错误. 故答案为:错误【分析】因为每一位上的数字都有10种可以选择,一共有两位数字不知道,因此根据乘法原理用10×10可以求出需要实验的密码的种类.
7.【答案】 正确
【解析】【解答】 从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数:50、52、57、20、25、27、70、72、75,原题说法正确. 故答案为:正确.
【分析】根据题意可知,4个数中除0之外,其他三个数都可以先放在十位上,十位上有3种不同情况;当十位数字确定后,个位数字也有3种不同的情况,一共可以组成3×3=9个两位数,据此判断.
8.【答案】 错误
【解析】【解答】解:8+7+6+5+4+3+2+1=36(条),原题说法错误。 故答案为:错误。 【分析】从第一个点可以引出8条线段,第二个点可以引出7条不重复的线段,……,倒数第二个点可以引出1条不重复的线段,把这些线段条数相加就是构成线段的总条数。
三、填空题
9.【答案】15;10
【解析】
10.【答案】 B
【解析】【解答】1+2+3+4+5=15(场)
故答案为:B。
【分析】因为彩用的是单循环赛,也就是每两支足球队之间都要进行一场比赛,所以共有15场比赛。
11.【答案】 D
【解析】【解答】库存10万升,表示库存的点应该在10万升处,A、B都是错误的;消毒液脱销,表示库存已经为0,C图形表示库存上升,是错误的,正确的是D.
故答案为:D
【分析】库存表示消毒液的量一直都是10万升,脱销表示库存已经没有了,也就是库存开始是稳定的,但是后来是0,由此判断并作出选择即可.
12.【答案】 9
【解析】【解答】3×3=9(个) 故答案为:9。 【分析】4个数中的3个数可以放到十位上,把其中一个数放到十位上,与剩下的3个数可以组成3个两位数,据此用乘法即可解答。
13.【答案】7;3;长方
【解析】
14.【答案】20;10
【解析】【解答】解法一:根据经验,知道任何两站之间都要准备两种不同的车票。如沈阳至长春这两站间既要准备沈阳→长春的车票,又要准备长春→沈阳的车票,这是两种不同的车票,但票价相同。因此每两个车站之间都要准备两种车票(只有一种票价)。因而此题可转化为沈阳至长春的线路上有多少条线段,就有多少种不同的票价,就需要准备线段数的2倍种车票。可以借助线段图来理解。 沈阳至长春的线段数为4+3+2+1=10(条),也就是有10种不同的票价。准备的车票共有10×2=20(种)。 解法二:因为每一个站点都可以直达另外四个站点。如A站点:A→B ??A→C ??A→D ???A→E,所以A站点需要准备4种车票,同理,其他站点也要各准备4种车票。这样5个站点就需准备5个4种车票。又因为同一段路往返票价相同,所以票价的种类是车票种类的一半。 5×(5-1)=20(种) ??20÷2=10(种) 答:共需要准备20种不同的车票,这些车票中共有10种不同的票价。 【分析】如果铁路沿线上有n个站点,就需要准备n×(n-1)种不同的车票。
四、解答题
15.【答案】解:
【解析】
16.【答案】解:(1)甲有7﹣3=4个位置 剩下6人的排列方法有: =6×5×4×3×2×1=720 4×720=2880(种) 答:甲不在中间也不在两端有2880种排列的方法. (2)2×× =2×(3×2×1)×(4×3×2×1) =2×6×24 =288(种) 答:男、女生分别排在一起一共有288种不同的方法. (3)× =(3×2×1)×(4×3×2×1) =6×24 =144(种) 答:男女相间一共有144种不同的方法.
【解析】【分析】(1)这是一个排列问题,先从受到限制的特殊元素进行考虑,先排甲有7﹣3=4种位置,剩下的6个元素全排列有种,根据分步计数原理得到结果; (2)把男女生分别看成一个元素,有2种排列的方法,男生和女生内部还有分别有一个全排列,然后再根据分步计数的原理进行求解; (3)先排男生有中方法,再将4个女生插在男生形成的4个空里,就有种方法,然后再根据分步计数的原理得到结果.
五、综合题
17.【答案】(1)2;1 (2)始终是1个圆,1个三角形,1个正方形,1个长方形。 (3)始终是后面一个数比前面一个数少2。 (4)始终是后面一个时钟比前面一个时钟快30分钟。 (5)
【解析】
六、应用题
18.【答案】解:42×4+18 =168+18 =186(个) 答:篮球有186个
【解析】【分析】足球有42个,篮球的个数比足球的4倍还多18个,求篮球有多少个?用足球的个数乘4再加上18即可.
19.【答案】30种
【解析】【解答】从男生中先出2名男生时,共有6种不同的选法,从3名女生中先2名女生时,共有3种不同的选法, 所以选2名男生一名女生时,共有3×6=18(种)选法 2名女生一名男生时,共有3×4=12(种)选法 18+12=30(种) 答:要求队员男女都有,有30种组队方案。 【分析】先确定出男生2名2名进行组合时的选法,女生2名2名组合时的选法,再确定出2名男生与一名女生组合时的选法,再确定出2名女生一名男生时的选法,然后再做进一步解答即可。
一、单选题
1.
二班可能有多少人(? )
A.?16人?????????????????????????????????????????B.?36人?????????????????????????????????????????C.?40人
2.从3名女生和2名男生中选出一对乒乓球混合双打选手,有多少种不同的组队方案
A.?9种???????????????????????????????????????B.?8种???????????????????????????????????????C.?7种???????????????????????????????????????D.?6种
3.小丽和父母到影楼照全家福,站成一排,他们有(??? )种排列方法。
A.?3??????????????????????????????????????????????B.?1??????????????????????????????????????????????C.?6
4.从 中任意选两个数相加,有(??? )种不同的和。
A.?3??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?5
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.一个有四位数的密码锁,忘记了首尾两个数字,则需要试验的密码有10种。
7.从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数。
8.在一条线段上共有9个点,则这9个点可以构成38条线段。( ??)
三、填空题
9.看图填数.? ________??-? 5=________
10.有6支班级代表队参加足球赛,若采用单循环赛制,则一共要赛(?? )
A.?16场?????????????????????????????????????B.?15场?????????????????????????????????????C.?5场?????????????????????????????????????D.?30场
11.开发区某消毒液生产厂家自2003年初以来,在库存为10万升的情况下,日销售量与产量持平,自4月底抗“非典”以来,消毒液的需求量猛增.在生产能力不变的情况下,消毒液一度脱销,以下表示2003年初至脱销期间,时间与库存量之间的关系的图象是(?? )
A.???????????????????????B.? C.??????????????????????????D.?
12.用 4张卡片能摆成________个两位数。
13.填空. 上图共有________个图形.从左边数起, 是第________个.从右边数起,第2个图形是________形.
14.某车次列车,在从沈阳至长春的铁路沿线上共停5站(包括沈阳、长春这两个车站).请问铁路局为这几个站点共需要准备________种不同的车票。这些车票中共有多________种不同的票价。
四、解答题
15.用彩笔涂出100个方格,想一想,涂10000个方格的纸有多大?
16.3名男生,4名女生,全体排成一行,问下列情形各有多少种不同的排法: (1)甲不在中间也不在两端; (2)男、女生分别排在一起; (3)男女相间.
五、综合题
17.我发现啦!??
(1)
我发现始终是________个 ,________个 。
(2)
我发现________。
(3)50 ?48 ?46 ?44 ?42 ?40
我发现________。
(4)
我发现________。
(5)我也会照样子画一组。________。
六、应用题
18.看图列式计算
19.为迎接2008年奥运会在北京召开,我校准备举行校羽毛球单打比赛.要求每班出2~3名选手参加比赛.六年三班有4名男同学和3名女同学报名参加,若从中派3名选手组队,要求队员男女都有,有多少种组队方案?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:二班人数比一班少,但是接近,所以二班的人数可以是36人.
故答案为:B.
【分析】二班人数比一班少一些,那么二班人数就应该比一班人数38人少,且比较接近38人,再结合给出的选项即可解答.本题主要考查学生:结合答案选项以及对多一些的知识了解情况.
2.【答案】 D
【解析】【解答】解:3×2=6(种)
故答案为:D。
【分析】一名女生与一名男生组合进行混合双打时,则有2种不同的组合方法,所以用3乘2即可求出3名女生与2名男生混合打时的组队方案。
3.【答案】 C
【解析】【解答】3×2=6(种) 故答案为:C。 【分析】可以这样想:小丽在最左边,其他两人交换后,有2种排列方法,同样其他两人在最左边时,又分别有2种排列方法,照相是排列有顺序的,因此用乘法即可解答。
4.【答案】 A
【解析】【解答】解:1+2=3,1+3=4,2+3=5,共3种不同的和。 故答案为:A。 【分析】把3个数字两两相加,分别求出和即可确定和的种类。
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】错误
【解析】【解答】解:10×10=100种,因此需要试验的密码有100种,原题说法错误. 故答案为:错误【分析】因为每一位上的数字都有10种可以选择,一共有两位数字不知道,因此根据乘法原理用10×10可以求出需要实验的密码的种类.
7.【答案】 正确
【解析】【解答】 从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数:50、52、57、20、25、27、70、72、75,原题说法正确. 故答案为:正确.
【分析】根据题意可知,4个数中除0之外,其他三个数都可以先放在十位上,十位上有3种不同情况;当十位数字确定后,个位数字也有3种不同的情况,一共可以组成3×3=9个两位数,据此判断.
8.【答案】 错误
【解析】【解答】解:8+7+6+5+4+3+2+1=36(条),原题说法错误。 故答案为:错误。 【分析】从第一个点可以引出8条线段,第二个点可以引出7条不重复的线段,……,倒数第二个点可以引出1条不重复的线段,把这些线段条数相加就是构成线段的总条数。
三、填空题
9.【答案】15;10
【解析】
10.【答案】 B
【解析】【解答】1+2+3+4+5=15(场)
故答案为:B。
【分析】因为彩用的是单循环赛,也就是每两支足球队之间都要进行一场比赛,所以共有15场比赛。
11.【答案】 D
【解析】【解答】库存10万升,表示库存的点应该在10万升处,A、B都是错误的;消毒液脱销,表示库存已经为0,C图形表示库存上升,是错误的,正确的是D.
故答案为:D
【分析】库存表示消毒液的量一直都是10万升,脱销表示库存已经没有了,也就是库存开始是稳定的,但是后来是0,由此判断并作出选择即可.
12.【答案】 9
【解析】【解答】3×3=9(个) 故答案为:9。 【分析】4个数中的3个数可以放到十位上,把其中一个数放到十位上,与剩下的3个数可以组成3个两位数,据此用乘法即可解答。
13.【答案】7;3;长方
【解析】
14.【答案】20;10
【解析】【解答】解法一:根据经验,知道任何两站之间都要准备两种不同的车票。如沈阳至长春这两站间既要准备沈阳→长春的车票,又要准备长春→沈阳的车票,这是两种不同的车票,但票价相同。因此每两个车站之间都要准备两种车票(只有一种票价)。因而此题可转化为沈阳至长春的线路上有多少条线段,就有多少种不同的票价,就需要准备线段数的2倍种车票。可以借助线段图来理解。 沈阳至长春的线段数为4+3+2+1=10(条),也就是有10种不同的票价。准备的车票共有10×2=20(种)。 解法二:因为每一个站点都可以直达另外四个站点。如A站点:A→B ??A→C ??A→D ???A→E,所以A站点需要准备4种车票,同理,其他站点也要各准备4种车票。这样5个站点就需准备5个4种车票。又因为同一段路往返票价相同,所以票价的种类是车票种类的一半。 5×(5-1)=20(种) ??20÷2=10(种) 答:共需要准备20种不同的车票,这些车票中共有10种不同的票价。 【分析】如果铁路沿线上有n个站点,就需要准备n×(n-1)种不同的车票。
四、解答题
15.【答案】解:
【解析】
16.【答案】解:(1)甲有7﹣3=4个位置 剩下6人的排列方法有: =6×5×4×3×2×1=720 4×720=2880(种) 答:甲不在中间也不在两端有2880种排列的方法. (2)2×× =2×(3×2×1)×(4×3×2×1) =2×6×24 =288(种) 答:男、女生分别排在一起一共有288种不同的方法. (3)× =(3×2×1)×(4×3×2×1) =6×24 =144(种) 答:男女相间一共有144种不同的方法.
【解析】【分析】(1)这是一个排列问题,先从受到限制的特殊元素进行考虑,先排甲有7﹣3=4种位置,剩下的6个元素全排列有种,根据分步计数原理得到结果; (2)把男女生分别看成一个元素,有2种排列的方法,男生和女生内部还有分别有一个全排列,然后再根据分步计数的原理进行求解; (3)先排男生有中方法,再将4个女生插在男生形成的4个空里,就有种方法,然后再根据分步计数的原理得到结果.
五、综合题
17.【答案】(1)2;1 (2)始终是1个圆,1个三角形,1个正方形,1个长方形。 (3)始终是后面一个数比前面一个数少2。 (4)始终是后面一个时钟比前面一个时钟快30分钟。 (5)
【解析】
六、应用题
18.【答案】解:42×4+18 =168+18 =186(个) 答:篮球有186个
【解析】【分析】足球有42个,篮球的个数比足球的4倍还多18个,求篮球有多少个?用足球的个数乘4再加上18即可.
19.【答案】30种
【解析】【解答】从男生中先出2名男生时,共有6种不同的选法,从3名女生中先2名女生时,共有3种不同的选法, 所以选2名男生一名女生时,共有3×6=18(种)选法 2名女生一名男生时,共有3×4=12(种)选法 18+12=30(种) 答:要求队员男女都有,有30种组队方案。 【分析】先确定出男生2名2名进行组合时的选法,女生2名2名组合时的选法,再确定出2名男生与一名女生组合时的选法,再确定出2名女生一名男生时的选法,然后再做进一步解答即可。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
