湘教版九年级数学下册第2章:2.4、过不共线三点作圆课件 (20张ppt)
文档属性
| 名称 | 湘教版九年级数学下册第2章:2.4、过不共线三点作圆课件 (20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 682.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 16:27:09 | ||
图片预览







文档简介
(共20张PPT)
第2章 圆
2.4过不共线三点作圆
【学习目标】
1.理解确定圆的条件及外接圆和外心的定义.
2.掌握三角形外接圆的画法.
【学习重点】
确定圆的条件及外接圆和外心的定义.
【学习难点】
任意三角形的外接圆的作法.
教学目标
情境引入:
下图中是一个破碎的圆盘,你能确定它的尺寸(圆盘的大小)吗?
确定圆的条件是什么?
圆心和半径
圆心确定圆的位置;半径确定圆的大小.
想一想:
做一做:
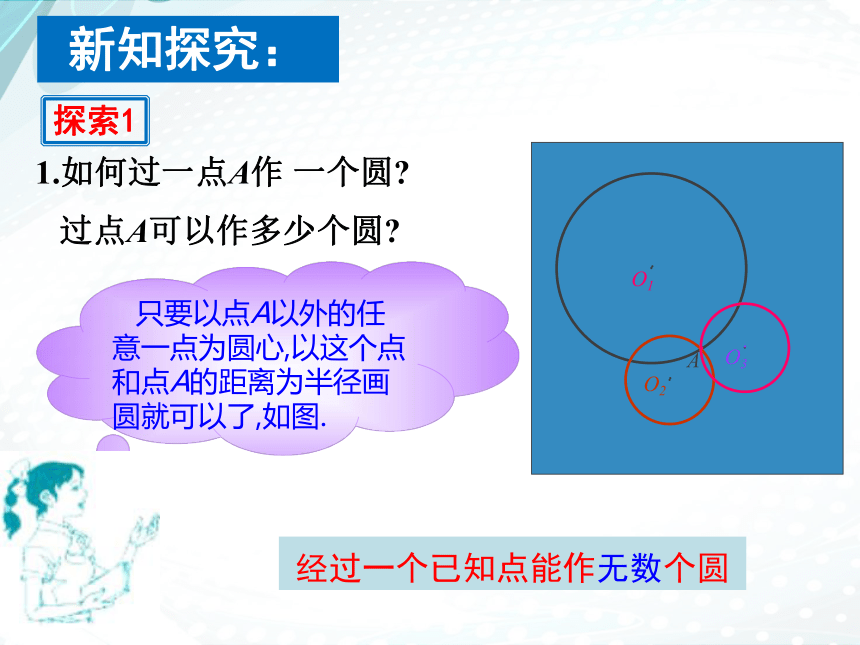
1.如何过一点A作 一个圆?过点A可以作多少个圆?
2.如何过两个点A、点B作圆?可以作多少个圆?
1.如何过一点A作 一个圆?
只要以点A以外的任意一点为圆心,以这个点和点A的距离为半径画圆就可以了,如图.
·
·
·
O1
O2
O3
过点A可以作多少个圆?
·
A
·
·
·
新知探究:
经过一个已知点能作无数个圆
探索1
·
·
·
·
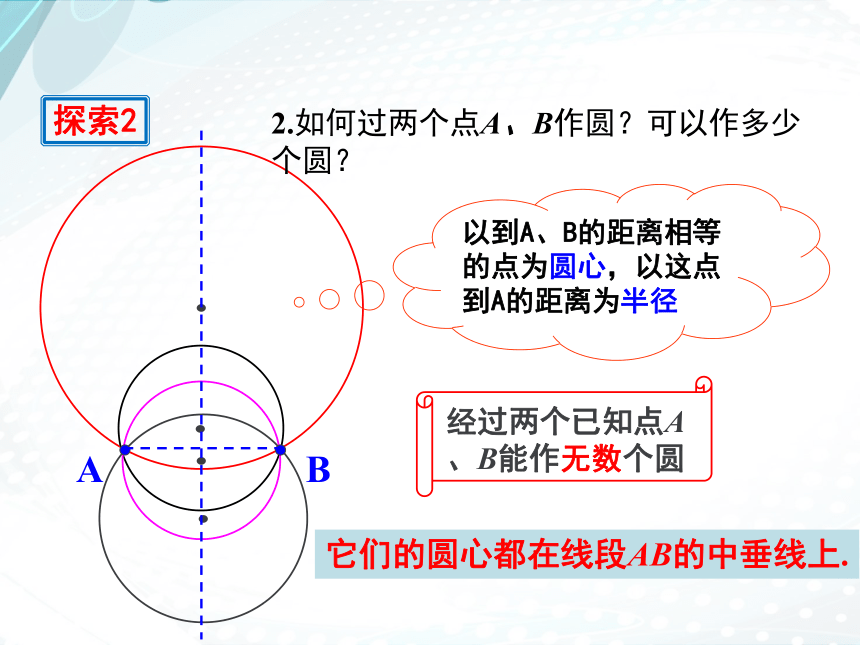
2.如何过两个点A、B作圆?可以作多少个圆?
A
B
经过两个已知点A、B能作无数个圆
以到A、B的距离相等的点为圆心,以这点到A的距离为半径
它们的圆心都在线段AB的中垂线上.
探索2
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
(填“相等”或“不相等”)。
(2)连结AB、AC,过O点 别作直线MN⊥AB, EF⊥AC,则MN是AB的 ; EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
动脑筋
如何过不在同一直线上的三个点作圆?
可以作多少个圆?
设三点A,B,C不在同一直线上.
⑴过三点A,B,C的圆的圆心在哪儿?
由于圆O与三点A,B,C的距离相等,因此圆心O既在线段AB的垂直平分线上,又在线段BC的垂直平分线上.
探索3
则圆O就是所求作的圆.
·
A
· O
B
· C
⑵过不在同一直线上的三点A,B,C如何作圆?
已知:不在同一直线上的三点A,B,C
求作:圆O,使它经过点A,B,C.
作法: ①连结AB,作线段AB的垂直平分线EF;
②连结BC,作线段BC的垂平分线MN;
③以EF和MN的交点O为圆心,以OB为半径作圆.
E
F
N
M
过点ABC三点的圆的圆心是线段AB、BC的垂直平分线的交点
过不在同一直线上的三点确定一个圆.
过不在同一直线上的三点可以作一个圆,并且只能作一个圆.
下图中是一个破碎的圆盘,你能确定它的尺寸(圆盘的大小)吗?
解决问题:
A
B
C
过在同一直线上的三点能不能作圆? 为什么?
不在同一直线上的三点确定一个圆
动脑筋
1.确定一个圆的条件有 ( )
①已知圆心和半径;②已知直径的位置和大小;③不在同一条直线上的三个点.
A.①② B.③ C.①②③ D.①
练一练
2.已知A,B两点间的距离为2 cm,则经过A,B两点,且半径为2 cm的圆能作 ( )
A.1个 B.2个 C.3个 D.无数个
C
B
已知△ABC,用直尺和圆规作出过点A、B、C的圆
A
B
C
O
做一做
由于△ABC的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
归纳总结:
1.画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思 考
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
随堂练习:
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
2..下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.三角形有且只有一个外接圆
D.圆有且只有一个内接三角形
C
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
3.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
4.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为 ( )
A.40° B.40°或140°
C.100° D.40°或100°
B
5.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________
(-1,-2)
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆.
(3)经过两个已知点A、B能作无数个圆。这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
谈谈你本节课的学习收获?
课堂总结:
第2章 圆
2.4过不共线三点作圆
【学习目标】
1.理解确定圆的条件及外接圆和外心的定义.
2.掌握三角形外接圆的画法.
【学习重点】
确定圆的条件及外接圆和外心的定义.
【学习难点】
任意三角形的外接圆的作法.
教学目标
情境引入:
下图中是一个破碎的圆盘,你能确定它的尺寸(圆盘的大小)吗?
确定圆的条件是什么?
圆心和半径
圆心确定圆的位置;半径确定圆的大小.
想一想:
做一做:
1.如何过一点A作 一个圆?过点A可以作多少个圆?
2.如何过两个点A、点B作圆?可以作多少个圆?
1.如何过一点A作 一个圆?
只要以点A以外的任意一点为圆心,以这个点和点A的距离为半径画圆就可以了,如图.
·
·
·
O1
O2
O3
过点A可以作多少个圆?
·
A
·
·
·
新知探究:
经过一个已知点能作无数个圆
探索1
·
·
·
·
2.如何过两个点A、B作圆?可以作多少个圆?
A
B
经过两个已知点A、B能作无数个圆
以到A、B的距离相等的点为圆心,以这点到A的距离为半径
它们的圆心都在线段AB的中垂线上.
探索2
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
(填“相等”或“不相等”)。
(2)连结AB、AC,过O点 别作直线MN⊥AB, EF⊥AC,则MN是AB的 ; EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
动脑筋
如何过不在同一直线上的三个点作圆?
可以作多少个圆?
设三点A,B,C不在同一直线上.
⑴过三点A,B,C的圆的圆心在哪儿?
由于圆O与三点A,B,C的距离相等,因此圆心O既在线段AB的垂直平分线上,又在线段BC的垂直平分线上.
探索3
则圆O就是所求作的圆.
·
A
· O
B
· C
⑵过不在同一直线上的三点A,B,C如何作圆?
已知:不在同一直线上的三点A,B,C
求作:圆O,使它经过点A,B,C.
作法: ①连结AB,作线段AB的垂直平分线EF;
②连结BC,作线段BC的垂平分线MN;
③以EF和MN的交点O为圆心,以OB为半径作圆.
E
F
N
M
过点ABC三点的圆的圆心是线段AB、BC的垂直平分线的交点
过不在同一直线上的三点确定一个圆.
过不在同一直线上的三点可以作一个圆,并且只能作一个圆.
下图中是一个破碎的圆盘,你能确定它的尺寸(圆盘的大小)吗?
解决问题:
A
B
C
过在同一直线上的三点能不能作圆? 为什么?
不在同一直线上的三点确定一个圆
动脑筋
1.确定一个圆的条件有 ( )
①已知圆心和半径;②已知直径的位置和大小;③不在同一条直线上的三个点.
A.①② B.③ C.①②③ D.①
练一练
2.已知A,B两点间的距离为2 cm,则经过A,B两点,且半径为2 cm的圆能作 ( )
A.1个 B.2个 C.3个 D.无数个
C
B
已知△ABC,用直尺和圆规作出过点A、B、C的圆
A
B
C
O
做一做
由于△ABC的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
归纳总结:
1.画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思 考
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
随堂练习:
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
2..下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.三角形有且只有一个外接圆
D.圆有且只有一个内接三角形
C
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
3.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
4.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为 ( )
A.40° B.40°或140°
C.100° D.40°或100°
B
5.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________
(-1,-2)
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆.
(3)经过两个已知点A、B能作无数个圆。这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
谈谈你本节课的学习收获?
课堂总结:
