2018-2019学年河北省保定十七中八年级(上)期末数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年河北省保定十七中八年级(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 07:20:48 | ||
图片预览


文档简介
2018-2019学年河北省保定十七中八年级(上)期末数学试卷
一、选择题(本大题共21个小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)实数﹣1,,3.1415926,﹣π,,3.,0,,0.2020020002……(相邻两个2之间0的个数逐次加1),,无理数的个数是( )
A.1 B.2 C.3 D.4
2.(2分)下列计算正确的是( )
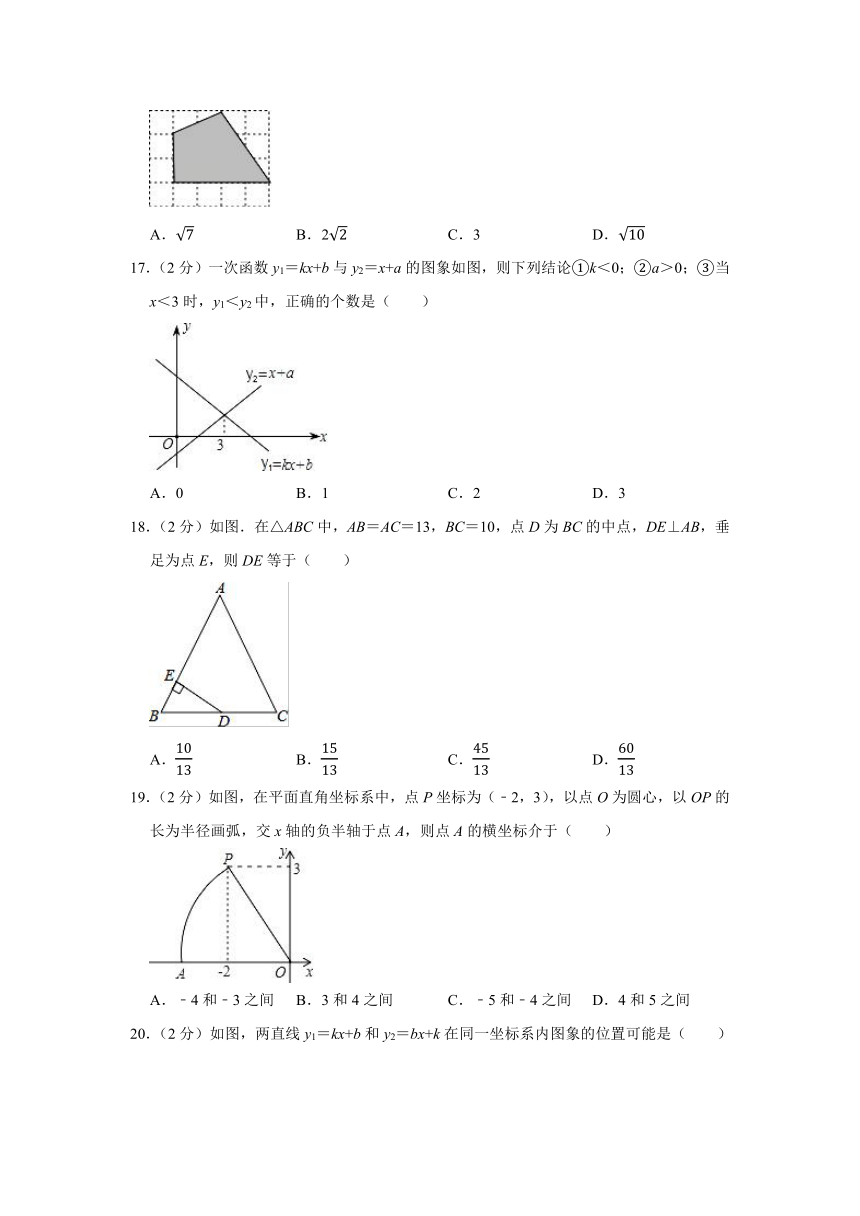
A.2 B.±4
C.2 D.2+3
3.(2分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
4.(2分)台风是一种破坏性极大的自然灾害,气象台为预报台风,首先确定它的位置,下列说法能确定台风位置是( )
A.北纬26°,东经133° B.西太平洋
C.距离台湾300海里 D.台湾与冲绳岛之间
5.(2分)下列图象表示y是x的函数的是( )
A. B.
C. D.
6.(2分)若点P(x,y)在第四象限内,且满足|x|=5,|y|=3,则点P的坐标是( )
A.(5,﹣3) B.(﹣5,3) C.(5,3) D.(﹣5,﹣3)
7.(2分)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣2,﹣4) C.(2,0) D.(0,﹣1.5)
8.(2分)下列语句:①﹣1是1的平方根.②带根号的数都是无理数.③﹣1的立方根是﹣1.④±4是64的立方根.⑤(﹣2)2的算术平方根2.⑥﹣125的立方根是±5.⑦有理数和数轴上的点一一对应.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
9.(2分)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣3)关于x轴对称,则m+n的值是( )
A.﹣1 B.1 C.5 D.﹣5
10.(2分)若5是一次函数,则a=( )
A.±3 B.3 C.﹣3 D.
11.(2分)函数y中自变量x的取值范围是( )
A.x≥0 B.x≥2 C.x≤2 D.x<2
12.(2分)在平面直角坐标系中,已知一次函数y=kx﹣1的图象经过第一、三、四象限,且经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则( )
A.y1<y2 B.y1>y2 C.y1=y2 D.不能确定
13.(2分)比较2,,的大小,正确的是( )
A. B. C. D.
14.(2分)如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是( )
A.6cm B.8cm C.10cm D.12cm
15.(2分)如图,在图中填上适当的数,使每一行、每一列、每一条对角线上的3个数的和都是0.则填在0右侧的数为( )
A. B. C. D.
16.(2分)如图,方格纸中每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A. B.2 C.3 D.
17.(2分)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
18.(2分)如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
19.(2分)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣4和﹣3之间 B.3和4之间 C.﹣5和﹣4之间 D.4和5之间
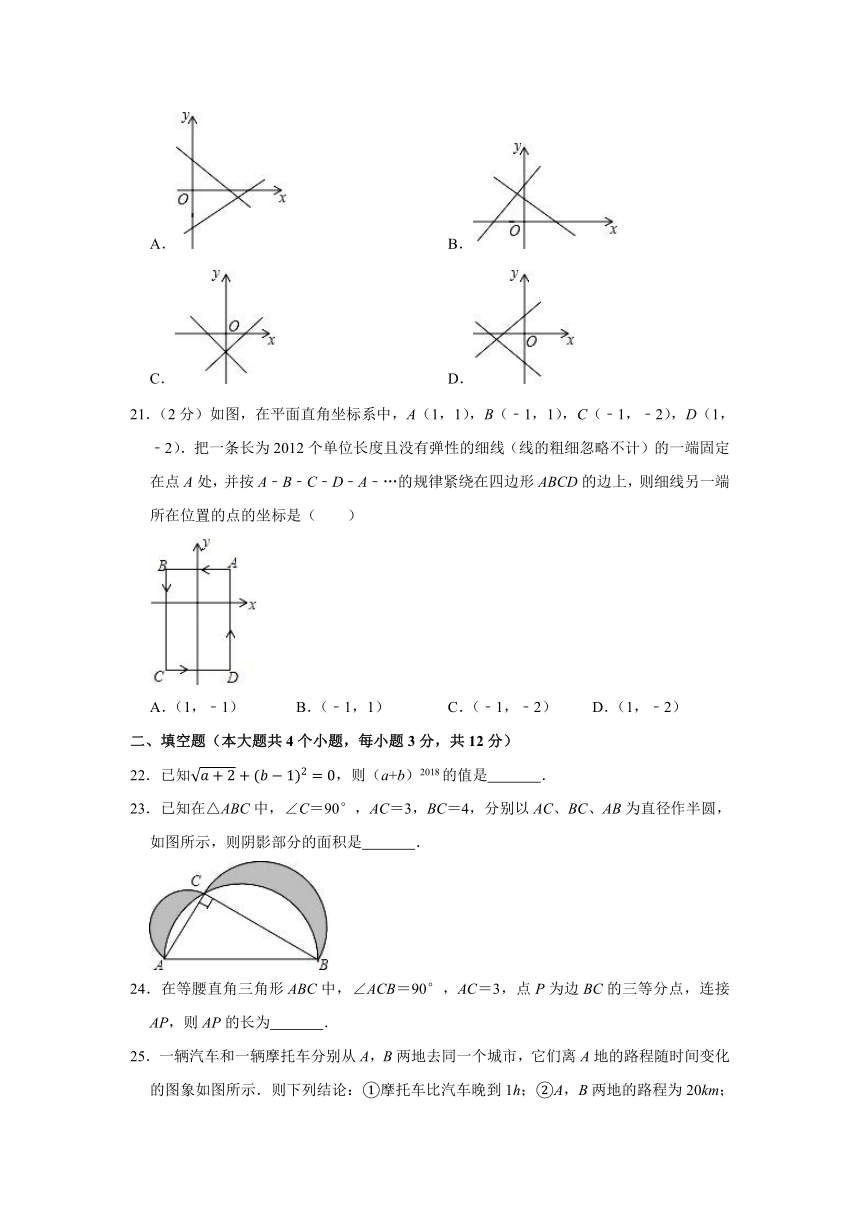
20.(2分)如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )
A. B.
C. D.
21.(2分)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣2) D.(1,﹣2)
二、填空题(本大题共4个小题,每小题3分,共12分)
22.已知,则(a+b)2018的值是 .
23.已知在△ABC中,∠C=90°,AC=3,BC=4,分别以AC、BC、AB为直径作半圆,如图所示,则阴影部分的面积是 .
24.在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为 .
25.一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论是 .(填序号)
三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程或演算步骤)
26.(25分)计算
(1)
(2)
(3)
(4)
(5)
27.(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)△ABC的周长是 ,面积是 ,AC边上的高是 ;
(2)在图中作出△ABC关于x轴对称的图形△A1B1C1,并写出△A1B1C1的顶点坐标.
A1: B1: C1: .
(3)请在y轴上找一点P,使得PA+PC的值最小,最小值是 .
28.阅读下列内容,试完成下列问题:
∵1<2<4,∴12.∴的整数部分是1,小数部分是1.
解决问题:的整数部分是 ,小数部分是 ;
拓展一:若9和9的小数部分分别是a和b,则a= ,b= .
拓展二:先阅读,再回答问题:
因为,且12,所以的整数部分为1;
因为,且12,所以的整数部分为2;
因为,且12,所以的整数部分为3;
以此类推,我们会发现的整数部分为 ,请简要说明理由.
29.“五?一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
请从下列两组题中任.选一组完成.多选者,按照A组题评分.
30.已知直线y1=﹣2x+6与x轴交于点A,与y轴交于点 B.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
(4)若直线l:y2=x与直线y1=﹣2x+6相交于点D,
①求点D的坐标;
②直接写出当y1>y2时x的取值范围.
③若存在直线a:y=kx+b平行于直线l,且与线段AB有公共点,直接写出k的值及b的取值范围.
31.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标;
(2)求折痕OE所在直线的解析式;
(3)若直线l:y=mx+n平行于直线OE,且与长方形ABMN有公共点,请直接写出n的取值范围.
(4)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2018-2019学年河北省保定十七中八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共21个小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)实数﹣1,,3.1415926,﹣π,,3.,0,,0.2020020002……(相邻两个2之间0的个数逐次加1),,无理数的个数是( )
A.1 B.2 C.3 D.4
【解答】解:﹣1是整数,属于有理数;,是整数,属于有理数;3.1415926是有限小数,属于有理数;,是整数,属于有理数;3.是循环小数,属于有理数;0是整数,属于有理数;是分数,属于有理数.
∴无理数有:﹣π,0.2020020002……(相邻两个2之间0的个数逐次加1),共3个.
故选:C.
2.(2分)下列计算正确的是( )
A.2 B.±4
C.2 D.2+3
【解答】解:A、2,故此选项符合题意;
B、4,故此选项不符合题意;
C、2,故此选项不符合题意;
D、,故此选项不符合题意.
故选:A.
3.(2分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
【解答】解:A、()2+()2≠()2,不能构成直角三角形,故错误;
B、12+()2=()2,能构成直角三角形,故正确;
C、62+72≠82,不能构成直角三角形,故错误;
D、22+32≠42,不能构成直角三角形,故错误.
故选:B.
4.(2分)台风是一种破坏性极大的自然灾害,气象台为预报台风,首先确定它的位置,下列说法能确定台风位置是( )
A.北纬26°,东经133° B.西太平洋
C.距离台湾300海里 D.台湾与冲绳岛之间
【解答】解:用西太平洋或距离台湾300海里或台湾与冲绳岛之间都不能确定台风位置,只有北纬26°,东经133°可确定台风位置.
故选:A.
5.(2分)下列图象表示y是x的函数的是( )
A. B.
C. D.
【解答】解:A、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
B、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
C、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
D、对每一个x的值,都有唯一确定的y值与之对应,是函数图象;
故选:D.
6.(2分)若点P(x,y)在第四象限内,且满足|x|=5,|y|=3,则点P的坐标是( )
A.(5,﹣3) B.(﹣5,3) C.(5,3) D.(﹣5,﹣3)
【解答】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
又∵|x|=5,|y|=3,
∴点P(x,y)坐标中,x=5,y=﹣3,
∴P点的坐标是(5,﹣3).
故选:A.
7.(2分)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣2,﹣4) C.(2,0) D.(0,﹣1.5)
【解答】解:∵x=﹣2时,y=3×(﹣2)+2=﹣4,
∴(﹣2,﹣4)在函数Y=3x+2上,
故选:B.
8.(2分)下列语句:①﹣1是1的平方根.②带根号的数都是无理数.③﹣1的立方根是﹣1.④±4是64的立方根.⑤(﹣2)2的算术平方根2.⑥﹣125的立方根是±5.⑦有理数和数轴上的点一一对应.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【解答】解:①﹣1是1的平方根,故符合题意;
②带根号的数不一定是无理数,故不符合题意;
③﹣1的立方根是﹣1,故符合题意;
④4是64的立方根,故不符合题意;
⑤(﹣2)2的算术平方根2,故符合题意;
⑥﹣125的立方根是﹣5,故不符合题意;
⑦实理数和数轴上的点一一对应,故不符合题意;
故选:B.
9.(2分)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣3)关于x轴对称,则m+n的值是( )
A.﹣1 B.1 C.5 D.﹣5
【解答】解:由点A(2,m)和点B(n,﹣3)关于x轴对称,得
n=2,m=3.
则m+n=2+3=5.
故选:C.
10.(2分)若5是一次函数,则a=( )
A.±3 B.3 C.﹣3 D.
【解答】解:根据一次函数的定义可知:a2﹣8=1,a+3≠0,
解得:a=3.
故选:B.
11.(2分)函数y中自变量x的取值范围是( )
A.x≥0 B.x≥2 C.x≤2 D.x<2
【解答】解:x﹣2≥0,
x≥2,
故选:B.
12.(2分)在平面直角坐标系中,已知一次函数y=kx﹣1的图象经过第一、三、四象限,且经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则( )
A.y1<y2 B.y1>y2 C.y1=y2 D.不能确定
【解答】解:∵一次函数y=kx﹣1的图象经过第一、三、四象限,
∴y随x值的增大而增大.
∵x1<x2,
∴y1<y2.
故选:A.
13.(2分)比较2,,的大小,正确的是( )
A. B. C. D.
【解答】解:∵23=8,()3=511.2,()3=7
∴2.
故选:C.
14.(2分)如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是( )
A.6cm B.8cm C.10cm D.12cm
【解答】解:底面周长为12cm,半圆弧长为6cm,
展开得:
又因为BC=8cm,AC=6cm,
根据勾股定理得:AB10(cm).
故选:C.
15.(2分)如图,在图中填上适当的数,使每一行、每一列、每一条对角线上的3个数的和都是0.则填在0右侧的数为( )
A. B. C. D.
【解答】解:如图:
,
故选:A.
16.(2分)如图,方格纸中每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A. B.2 C.3 D.
【解答】解:阴影部分的面积为:S阴影=3×41×22×3=8,
∵新正方形的边长2=S阴影,
∴新正方形的边长=2.
故选:B.
17.(2分)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
【解答】解:∵y1=kx+b的函数值随x的增大而减小,
∴k<0;故①正确
∵y2=x+a的图象与y轴交于负半轴,
∴a<0;
当x<3时,相应的x的值,y1图象均高于y2的图象,
∴y1>y2,故②③错误.
故选:B.
18.(2分)如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
【解答】解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BDBC=5,
∴AD12,
又∵DE⊥AB,
∴BD?ADAB?ED,
∴ED,
故选:D.
19.(2分)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣4和﹣3之间 B.3和4之间 C.﹣5和﹣4之间 D.4和5之间
【解答】解:∵点P坐标为(﹣2,3),
∴OP,
∵点A、P均在以点O为圆心,以OP为半径的圆上,
∴OA=OP,
∵9<13<16,
∴34.
∵点A在x轴的负半轴上,
∴点A的横坐标介于﹣4和﹣3之间.
故选:A.
20.(2分)如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )
A. B.
C. D.
【解答】解:根据一次函数的系数与图象的关系依次分析选项可得:
A、由图可得,y1=kx+b中,k<0,b>0,y2=bx+k中,b>0,k<0,符合;
B、由图可得,y1=kx+b中,k>0,b>0,y2=bx+k中,b<0,k>0,不符合;
C、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k<0,不符合;
D、由图可得,y1=kx+b中,k>0,b>0,y2=bx+k中,b<0,k<0,不符合;
故选:A.
21.(2分)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣2) D.(1,﹣2)
【解答】解:∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2012÷10=201…2,
∴细线另一端在绕四边形第202圈的第2个单位长度的位置,
即点B的位置,点的坐标为(﹣1,1).
故选:B.
二、填空题(本大题共4个小题,每小题3分,共12分)
22.已知,则(a+b)2018的值是 1 .
【解答】解:根据题意得,a+2=0,b﹣1=0,
解得a=﹣2,b=1,
所以,(a+b)2018=(﹣2+1)2018=1.
故答案为:1.
23.已知在△ABC中,∠C=90°,AC=3,BC=4,分别以AC、BC、AB为直径作半圆,如图所示,则阴影部分的面积是 6 .
【解答】解:∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵BC=4,AC=3,
∴AB.
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC﹣直径为AB的半圆的面积
π()2π()2AC×BCπ()2
π(AC)2π(BC)2π(AB)2AC×BC
π(AC2+BC2﹣AB2)AC×BC
AC×BC
3×4
=6.
故答案为:6
24.在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为 或 .
【解答】解:①如图1,∵∠ACB=90°,AC=BC=3,
∵PBBC=1,
∴CP=2,
∴AP,
②如图2,∵∠ACB=90°,AC=BC=3,
∵PCBC=1,
∴AP,
综上所述:AP的长为或,
故答案为:或.
25.一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论是 ①②④ .(填序号)
【解答】解:摩托车比汽车晚到:4﹣3=1h,故①正确,
A、B两地的路程为20km,故②正确,
摩托车的速度为(180﹣20)÷4=40km/h,汽车的速度为180÷3=60km/h,故③错误,
设汽车出x小时与摩托车相遇,则60x=20+40x,得x=1,此时距离B地40×1=40km,故④正确,
故答案为:①②④.
三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程或演算步骤)
26.(25分)计算
(1)
(2)
(3)
(4)
(5)
【解答】解:(1)
=8﹣5
=3;
(2)
=5﹣6
=﹣1;
(3)
=3+3﹣1
=5;
(4)
=2﹣6﹣4
=﹣8;
(5)
=2
.
27.(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)△ABC的周长是 5 ,面积是 3 ,AC边上的高是 ;
(2)在图中作出△ABC关于x轴对称的图形△A1B1C1,并写出△A1B1C1的顶点坐标.
A1: (﹣3,0) B1: (﹣3,3) C1: (﹣1,3) .
(3)请在y轴上找一点P,使得PA+PC的值最小,最小值是 5 .
【解答】解:(1)△ABC的周长是:2+35,面积是:2×3=3,
AC边上的高是:h=3,则h;
故答案为:5,3,;
(2)如图所示:A1:(﹣3,0),B1:(﹣3,3),C1:(﹣1,3);
故答案为:(﹣3,0),(﹣3,3),(﹣1,3);
(3)PA+PC的值最小值是:5.
故答案为:5.
28.阅读下列内容,试完成下列问题:
∵1<2<4,∴12.∴的整数部分是1,小数部分是1.
解决问题:的整数部分是 3 ,小数部分是 3 ;
拓展一:若9和9的小数部分分别是a和b,则a= 3 ,b= 4 .
拓展二:先阅读,再回答问题:
因为,且12,所以的整数部分为1;
因为,且12,所以的整数部分为2;
因为,且12,所以的整数部分为3;
以此类推,我们会发现的整数部分为 n ,请简要说明理由.
【解答】解:∵34,
∴的整数部分是3,小数部分是3;
∵9和9的小数部分分别是a和b,
∴a=99﹣33,
b=95=4;
∵的整数部分为1;
的整数部分为2;
的整数部分为3;
n2<n2+n<(n+1)2=n2+2n+1,
∴(n为正整数)的整数部分为n.
故答案为:3,3;3,4;n.
29.“五?一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
【解答】解:(1)设y1=k1x+80,
把点(1,95)代入,可得
95=k1+80,
解得k1=15,
∴y1=15x+80(x≥0);
设y2=k2x,
把(1,30)代入,可得
30=k2,即k2=30,
∴y2=30x(x≥0);
(2)当y1=y2时,15x+80=30x,
解得x;
当y1>y2时,15x+80>30x,
解得x;
当y1<y2时,15x+80<30x,
解得x;
∴当租车时间为小时,选择甲乙公司一样合算;当租车时间小于小时,选择乙公司合算;当租车时间大于小时,选择甲公司合算.
请从下列两组题中任.选一组完成.多选者,按照A组题评分.
30.已知直线y1=﹣2x+6与x轴交于点A,与y轴交于点 B.
(1)点A的坐标为 (3,0) ,点B的坐标为 (0,6) ;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
(4)若直线l:y2=x与直线y1=﹣2x+6相交于点D,
①求点D的坐标;
②直接写出当y1>y2时x的取值范围.
③若存在直线a:y=kx+b平行于直线l,且与线段AB有公共点,直接写出k的值及b的取值范围.
【解答】解:(1)当y=0时,﹣2x+6=0
解得:x=3
∴A(3,0);
当x=0时,y=﹣2x+6=6
∴B(0,6).
故答案为:(3,0),;(0,6).
(2)△AOB的面积为:3×6=9.
(3)存在.
设C(t,﹣2t+6)
∵△AOC的面积等于△AOB的面积
∴3×|﹣2t+6|=9
解得:t1=6,t2=0(舍去)
∴C点坐标为(6,﹣6).
(4)①∵y2=x与直线y1=﹣2x+6相交于点D
∴x=﹣2x+6
∴x=2,y=2
∴点D的坐标为:(2,2).
②当y1>y2时x的取值范围为:x<2;
③直线a:y=kx+b平行于直线l:y2=x
∴k=1;
∵A(3,0),B(0,6)
∴直线a:y=kx+b与线段AB有公共点时,
﹣6≤b≤3.
∴符合题意的k的值为1,b的取值范围为﹣6≤b≤3.
31.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标;
(2)求折痕OE所在直线的解析式;
(3)若直线l:y=mx+n平行于直线OE,且与长方形ABMN有公共点,请直接写出n的取值范围.
(4)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)由折叠的性质可知,OG=OC=5,
由勾股定理得,GN4,
∴点G的坐标为(3,4);
(2)设CE=x,则EM=3﹣x,
由折叠的性质可知,EG=CE=x,
∵GN=4,
∴GM=5﹣4=1,
在Rt△EMG中,EG2=EM2+MG2,即x2=(3﹣x)2+12,
解得,x,
∴点E的坐标为(,5),
设OE所在直线的解析式为:y=kx,
则k=5,
解得,k=3,
∴OE所在直线的解析式为:y=3x;
(3)∵直线l:y=mx+n平行于直线OE,
∴m=3,即直线l的解析式为y=3x+n,
当直线l经过点M(3,5)时,5=3×3+n,
解得,n=﹣4,
当直线l经过点A(5,5)时,5=3×5+n,
解得,n=﹣10,
∴直线l与长方形ABMN有公共点时,﹣10≤n≤﹣4;
(4)当OP=OG=5,点P在原点左侧时,点P的坐标为(﹣5,0),
点P在原点左侧时,点P的坐标为(5,0),
当GP=GO时,GN⊥OP,
∴NP=NO=3,
∴OP=6,
∴点P的坐标为(6,0),
作PQ垂直平分OG交x轴于P,则PO=PG,
∴PN=OP﹣ON=OP﹣3,
在Rt△GPN中,PG2=GN2+PN2,即OP2=(OP﹣3)2+42,
解得,OP,
∴点P的坐标为(,0),
综上所述,以P,O,G为顶点的三角形为等腰三角形时,点P的坐标为(5,0)或(﹣5,0)或(6,0)或(,0).
一、选择题(本大题共21个小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)实数﹣1,,3.1415926,﹣π,,3.,0,,0.2020020002……(相邻两个2之间0的个数逐次加1),,无理数的个数是( )
A.1 B.2 C.3 D.4
2.(2分)下列计算正确的是( )
A.2 B.±4
C.2 D.2+3
3.(2分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
4.(2分)台风是一种破坏性极大的自然灾害,气象台为预报台风,首先确定它的位置,下列说法能确定台风位置是( )
A.北纬26°,东经133° B.西太平洋
C.距离台湾300海里 D.台湾与冲绳岛之间
5.(2分)下列图象表示y是x的函数的是( )
A. B.
C. D.
6.(2分)若点P(x,y)在第四象限内,且满足|x|=5,|y|=3,则点P的坐标是( )
A.(5,﹣3) B.(﹣5,3) C.(5,3) D.(﹣5,﹣3)
7.(2分)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣2,﹣4) C.(2,0) D.(0,﹣1.5)
8.(2分)下列语句:①﹣1是1的平方根.②带根号的数都是无理数.③﹣1的立方根是﹣1.④±4是64的立方根.⑤(﹣2)2的算术平方根2.⑥﹣125的立方根是±5.⑦有理数和数轴上的点一一对应.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
9.(2分)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣3)关于x轴对称,则m+n的值是( )
A.﹣1 B.1 C.5 D.﹣5
10.(2分)若5是一次函数,则a=( )
A.±3 B.3 C.﹣3 D.
11.(2分)函数y中自变量x的取值范围是( )
A.x≥0 B.x≥2 C.x≤2 D.x<2
12.(2分)在平面直角坐标系中,已知一次函数y=kx﹣1的图象经过第一、三、四象限,且经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则( )
A.y1<y2 B.y1>y2 C.y1=y2 D.不能确定
13.(2分)比较2,,的大小,正确的是( )
A. B. C. D.
14.(2分)如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是( )
A.6cm B.8cm C.10cm D.12cm
15.(2分)如图,在图中填上适当的数,使每一行、每一列、每一条对角线上的3个数的和都是0.则填在0右侧的数为( )
A. B. C. D.
16.(2分)如图,方格纸中每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A. B.2 C.3 D.
17.(2分)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
18.(2分)如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
19.(2分)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣4和﹣3之间 B.3和4之间 C.﹣5和﹣4之间 D.4和5之间
20.(2分)如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )
A. B.
C. D.
21.(2分)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣2) D.(1,﹣2)
二、填空题(本大题共4个小题,每小题3分,共12分)
22.已知,则(a+b)2018的值是 .
23.已知在△ABC中,∠C=90°,AC=3,BC=4,分别以AC、BC、AB为直径作半圆,如图所示,则阴影部分的面积是 .
24.在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为 .
25.一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论是 .(填序号)
三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程或演算步骤)
26.(25分)计算
(1)
(2)
(3)
(4)
(5)
27.(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)△ABC的周长是 ,面积是 ,AC边上的高是 ;
(2)在图中作出△ABC关于x轴对称的图形△A1B1C1,并写出△A1B1C1的顶点坐标.
A1: B1: C1: .
(3)请在y轴上找一点P,使得PA+PC的值最小,最小值是 .
28.阅读下列内容,试完成下列问题:
∵1<2<4,∴12.∴的整数部分是1,小数部分是1.
解决问题:的整数部分是 ,小数部分是 ;
拓展一:若9和9的小数部分分别是a和b,则a= ,b= .
拓展二:先阅读,再回答问题:
因为,且12,所以的整数部分为1;
因为,且12,所以的整数部分为2;
因为,且12,所以的整数部分为3;
以此类推,我们会发现的整数部分为 ,请简要说明理由.
29.“五?一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
请从下列两组题中任.选一组完成.多选者,按照A组题评分.
30.已知直线y1=﹣2x+6与x轴交于点A,与y轴交于点 B.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
(4)若直线l:y2=x与直线y1=﹣2x+6相交于点D,
①求点D的坐标;
②直接写出当y1>y2时x的取值范围.
③若存在直线a:y=kx+b平行于直线l,且与线段AB有公共点,直接写出k的值及b的取值范围.
31.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标;
(2)求折痕OE所在直线的解析式;
(3)若直线l:y=mx+n平行于直线OE,且与长方形ABMN有公共点,请直接写出n的取值范围.
(4)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2018-2019学年河北省保定十七中八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共21个小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)实数﹣1,,3.1415926,﹣π,,3.,0,,0.2020020002……(相邻两个2之间0的个数逐次加1),,无理数的个数是( )
A.1 B.2 C.3 D.4
【解答】解:﹣1是整数,属于有理数;,是整数,属于有理数;3.1415926是有限小数,属于有理数;,是整数,属于有理数;3.是循环小数,属于有理数;0是整数,属于有理数;是分数,属于有理数.
∴无理数有:﹣π,0.2020020002……(相邻两个2之间0的个数逐次加1),共3个.
故选:C.
2.(2分)下列计算正确的是( )
A.2 B.±4
C.2 D.2+3
【解答】解:A、2,故此选项符合题意;
B、4,故此选项不符合题意;
C、2,故此选项不符合题意;
D、,故此选项不符合题意.
故选:A.
3.(2分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
【解答】解:A、()2+()2≠()2,不能构成直角三角形,故错误;
B、12+()2=()2,能构成直角三角形,故正确;
C、62+72≠82,不能构成直角三角形,故错误;
D、22+32≠42,不能构成直角三角形,故错误.
故选:B.
4.(2分)台风是一种破坏性极大的自然灾害,气象台为预报台风,首先确定它的位置,下列说法能确定台风位置是( )
A.北纬26°,东经133° B.西太平洋
C.距离台湾300海里 D.台湾与冲绳岛之间
【解答】解:用西太平洋或距离台湾300海里或台湾与冲绳岛之间都不能确定台风位置,只有北纬26°,东经133°可确定台风位置.
故选:A.
5.(2分)下列图象表示y是x的函数的是( )
A. B.
C. D.
【解答】解:A、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
B、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
C、对每一个x的值,不是有唯一确定的y值与之对应,不是函数图象;
D、对每一个x的值,都有唯一确定的y值与之对应,是函数图象;
故选:D.
6.(2分)若点P(x,y)在第四象限内,且满足|x|=5,|y|=3,则点P的坐标是( )
A.(5,﹣3) B.(﹣5,3) C.(5,3) D.(﹣5,﹣3)
【解答】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
又∵|x|=5,|y|=3,
∴点P(x,y)坐标中,x=5,y=﹣3,
∴P点的坐标是(5,﹣3).
故选:A.
7.(2分)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣2,﹣4) C.(2,0) D.(0,﹣1.5)
【解答】解:∵x=﹣2时,y=3×(﹣2)+2=﹣4,
∴(﹣2,﹣4)在函数Y=3x+2上,
故选:B.
8.(2分)下列语句:①﹣1是1的平方根.②带根号的数都是无理数.③﹣1的立方根是﹣1.④±4是64的立方根.⑤(﹣2)2的算术平方根2.⑥﹣125的立方根是±5.⑦有理数和数轴上的点一一对应.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【解答】解:①﹣1是1的平方根,故符合题意;
②带根号的数不一定是无理数,故不符合题意;
③﹣1的立方根是﹣1,故符合题意;
④4是64的立方根,故不符合题意;
⑤(﹣2)2的算术平方根2,故符合题意;
⑥﹣125的立方根是﹣5,故不符合题意;
⑦实理数和数轴上的点一一对应,故不符合题意;
故选:B.
9.(2分)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣3)关于x轴对称,则m+n的值是( )
A.﹣1 B.1 C.5 D.﹣5
【解答】解:由点A(2,m)和点B(n,﹣3)关于x轴对称,得
n=2,m=3.
则m+n=2+3=5.
故选:C.
10.(2分)若5是一次函数,则a=( )
A.±3 B.3 C.﹣3 D.
【解答】解:根据一次函数的定义可知:a2﹣8=1,a+3≠0,
解得:a=3.
故选:B.
11.(2分)函数y中自变量x的取值范围是( )
A.x≥0 B.x≥2 C.x≤2 D.x<2
【解答】解:x﹣2≥0,
x≥2,
故选:B.
12.(2分)在平面直角坐标系中,已知一次函数y=kx﹣1的图象经过第一、三、四象限,且经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则( )
A.y1<y2 B.y1>y2 C.y1=y2 D.不能确定
【解答】解:∵一次函数y=kx﹣1的图象经过第一、三、四象限,
∴y随x值的增大而增大.
∵x1<x2,
∴y1<y2.
故选:A.
13.(2分)比较2,,的大小,正确的是( )
A. B. C. D.
【解答】解:∵23=8,()3=511.2,()3=7
∴2.
故选:C.
14.(2分)如图,一圆柱高8cm,底面周长为12cm,一只蚂蚁从A点爬到点B,要爬行的最短路程是( )
A.6cm B.8cm C.10cm D.12cm
【解答】解:底面周长为12cm,半圆弧长为6cm,
展开得:
又因为BC=8cm,AC=6cm,
根据勾股定理得:AB10(cm).
故选:C.
15.(2分)如图,在图中填上适当的数,使每一行、每一列、每一条对角线上的3个数的和都是0.则填在0右侧的数为( )
A. B. C. D.
【解答】解:如图:
,
故选:A.
16.(2分)如图,方格纸中每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A. B.2 C.3 D.
【解答】解:阴影部分的面积为:S阴影=3×41×22×3=8,
∵新正方形的边长2=S阴影,
∴新正方形的边长=2.
故选:B.
17.(2分)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
【解答】解:∵y1=kx+b的函数值随x的增大而减小,
∴k<0;故①正确
∵y2=x+a的图象与y轴交于负半轴,
∴a<0;
当x<3时,相应的x的值,y1图象均高于y2的图象,
∴y1>y2,故②③错误.
故选:B.
18.(2分)如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
【解答】解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BDBC=5,
∴AD12,
又∵DE⊥AB,
∴BD?ADAB?ED,
∴ED,
故选:D.
19.(2分)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣4和﹣3之间 B.3和4之间 C.﹣5和﹣4之间 D.4和5之间
【解答】解:∵点P坐标为(﹣2,3),
∴OP,
∵点A、P均在以点O为圆心,以OP为半径的圆上,
∴OA=OP,
∵9<13<16,
∴34.
∵点A在x轴的负半轴上,
∴点A的横坐标介于﹣4和﹣3之间.
故选:A.
20.(2分)如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )
A. B.
C. D.
【解答】解:根据一次函数的系数与图象的关系依次分析选项可得:
A、由图可得,y1=kx+b中,k<0,b>0,y2=bx+k中,b>0,k<0,符合;
B、由图可得,y1=kx+b中,k>0,b>0,y2=bx+k中,b<0,k>0,不符合;
C、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k<0,不符合;
D、由图可得,y1=kx+b中,k>0,b>0,y2=bx+k中,b<0,k<0,不符合;
故选:A.
21.(2分)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣2) D.(1,﹣2)
【解答】解:∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2012÷10=201…2,
∴细线另一端在绕四边形第202圈的第2个单位长度的位置,
即点B的位置,点的坐标为(﹣1,1).
故选:B.
二、填空题(本大题共4个小题,每小题3分,共12分)
22.已知,则(a+b)2018的值是 1 .
【解答】解:根据题意得,a+2=0,b﹣1=0,
解得a=﹣2,b=1,
所以,(a+b)2018=(﹣2+1)2018=1.
故答案为:1.
23.已知在△ABC中,∠C=90°,AC=3,BC=4,分别以AC、BC、AB为直径作半圆,如图所示,则阴影部分的面积是 6 .
【解答】解:∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵BC=4,AC=3,
∴AB.
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC﹣直径为AB的半圆的面积
π()2π()2AC×BCπ()2
π(AC)2π(BC)2π(AB)2AC×BC
π(AC2+BC2﹣AB2)AC×BC
AC×BC
3×4
=6.
故答案为:6
24.在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为 或 .
【解答】解:①如图1,∵∠ACB=90°,AC=BC=3,
∵PBBC=1,
∴CP=2,
∴AP,
②如图2,∵∠ACB=90°,AC=BC=3,
∵PCBC=1,
∴AP,
综上所述:AP的长为或,
故答案为:或.
25.一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论是 ①②④ .(填序号)
【解答】解:摩托车比汽车晚到:4﹣3=1h,故①正确,
A、B两地的路程为20km,故②正确,
摩托车的速度为(180﹣20)÷4=40km/h,汽车的速度为180÷3=60km/h,故③错误,
设汽车出x小时与摩托车相遇,则60x=20+40x,得x=1,此时距离B地40×1=40km,故④正确,
故答案为:①②④.
三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程或演算步骤)
26.(25分)计算
(1)
(2)
(3)
(4)
(5)
【解答】解:(1)
=8﹣5
=3;
(2)
=5﹣6
=﹣1;
(3)
=3+3﹣1
=5;
(4)
=2﹣6﹣4
=﹣8;
(5)
=2
.
27.(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)△ABC的周长是 5 ,面积是 3 ,AC边上的高是 ;
(2)在图中作出△ABC关于x轴对称的图形△A1B1C1,并写出△A1B1C1的顶点坐标.
A1: (﹣3,0) B1: (﹣3,3) C1: (﹣1,3) .
(3)请在y轴上找一点P,使得PA+PC的值最小,最小值是 5 .
【解答】解:(1)△ABC的周长是:2+35,面积是:2×3=3,
AC边上的高是:h=3,则h;
故答案为:5,3,;
(2)如图所示:A1:(﹣3,0),B1:(﹣3,3),C1:(﹣1,3);
故答案为:(﹣3,0),(﹣3,3),(﹣1,3);
(3)PA+PC的值最小值是:5.
故答案为:5.
28.阅读下列内容,试完成下列问题:
∵1<2<4,∴12.∴的整数部分是1,小数部分是1.
解决问题:的整数部分是 3 ,小数部分是 3 ;
拓展一:若9和9的小数部分分别是a和b,则a= 3 ,b= 4 .
拓展二:先阅读,再回答问题:
因为,且12,所以的整数部分为1;
因为,且12,所以的整数部分为2;
因为,且12,所以的整数部分为3;
以此类推,我们会发现的整数部分为 n ,请简要说明理由.
【解答】解:∵34,
∴的整数部分是3,小数部分是3;
∵9和9的小数部分分别是a和b,
∴a=99﹣33,
b=95=4;
∵的整数部分为1;
的整数部分为2;
的整数部分为3;
n2<n2+n<(n+1)2=n2+2n+1,
∴(n为正整数)的整数部分为n.
故答案为:3,3;3,4;n.
29.“五?一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
【解答】解:(1)设y1=k1x+80,
把点(1,95)代入,可得
95=k1+80,
解得k1=15,
∴y1=15x+80(x≥0);
设y2=k2x,
把(1,30)代入,可得
30=k2,即k2=30,
∴y2=30x(x≥0);
(2)当y1=y2时,15x+80=30x,
解得x;
当y1>y2时,15x+80>30x,
解得x;
当y1<y2时,15x+80<30x,
解得x;
∴当租车时间为小时,选择甲乙公司一样合算;当租车时间小于小时,选择乙公司合算;当租车时间大于小时,选择甲公司合算.
请从下列两组题中任.选一组完成.多选者,按照A组题评分.
30.已知直线y1=﹣2x+6与x轴交于点A,与y轴交于点 B.
(1)点A的坐标为 (3,0) ,点B的坐标为 (0,6) ;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
(4)若直线l:y2=x与直线y1=﹣2x+6相交于点D,
①求点D的坐标;
②直接写出当y1>y2时x的取值范围.
③若存在直线a:y=kx+b平行于直线l,且与线段AB有公共点,直接写出k的值及b的取值范围.
【解答】解:(1)当y=0时,﹣2x+6=0
解得:x=3
∴A(3,0);
当x=0时,y=﹣2x+6=6
∴B(0,6).
故答案为:(3,0),;(0,6).
(2)△AOB的面积为:3×6=9.
(3)存在.
设C(t,﹣2t+6)
∵△AOC的面积等于△AOB的面积
∴3×|﹣2t+6|=9
解得:t1=6,t2=0(舍去)
∴C点坐标为(6,﹣6).
(4)①∵y2=x与直线y1=﹣2x+6相交于点D
∴x=﹣2x+6
∴x=2,y=2
∴点D的坐标为:(2,2).
②当y1>y2时x的取值范围为:x<2;
③直线a:y=kx+b平行于直线l:y2=x
∴k=1;
∵A(3,0),B(0,6)
∴直线a:y=kx+b与线段AB有公共点时,
﹣6≤b≤3.
∴符合题意的k的值为1,b的取值范围为﹣6≤b≤3.
31.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标;
(2)求折痕OE所在直线的解析式;
(3)若直线l:y=mx+n平行于直线OE,且与长方形ABMN有公共点,请直接写出n的取值范围.
(4)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)由折叠的性质可知,OG=OC=5,
由勾股定理得,GN4,
∴点G的坐标为(3,4);
(2)设CE=x,则EM=3﹣x,
由折叠的性质可知,EG=CE=x,
∵GN=4,
∴GM=5﹣4=1,
在Rt△EMG中,EG2=EM2+MG2,即x2=(3﹣x)2+12,
解得,x,
∴点E的坐标为(,5),
设OE所在直线的解析式为:y=kx,
则k=5,
解得,k=3,
∴OE所在直线的解析式为:y=3x;
(3)∵直线l:y=mx+n平行于直线OE,
∴m=3,即直线l的解析式为y=3x+n,
当直线l经过点M(3,5)时,5=3×3+n,
解得,n=﹣4,
当直线l经过点A(5,5)时,5=3×5+n,
解得,n=﹣10,
∴直线l与长方形ABMN有公共点时,﹣10≤n≤﹣4;
(4)当OP=OG=5,点P在原点左侧时,点P的坐标为(﹣5,0),
点P在原点左侧时,点P的坐标为(5,0),
当GP=GO时,GN⊥OP,
∴NP=NO=3,
∴OP=6,
∴点P的坐标为(6,0),
作PQ垂直平分OG交x轴于P,则PO=PG,
∴PN=OP﹣ON=OP﹣3,
在Rt△GPN中,PG2=GN2+PN2,即OP2=(OP﹣3)2+42,
解得,OP,
∴点P的坐标为(,0),
综上所述,以P,O,G为顶点的三角形为等腰三角形时,点P的坐标为(5,0)或(﹣5,0)或(6,0)或(,0).
同课章节目录
