人教版七年级上册数学 3.1.2 等式的性质课件 (共34张PPT)
文档属性
| 名称 | 人教版七年级上册数学 3.1.2 等式的性质课件 (共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 21:33:06 | ||
图片预览






文档简介
(共34张PPT)
3.1.2 等式的性质
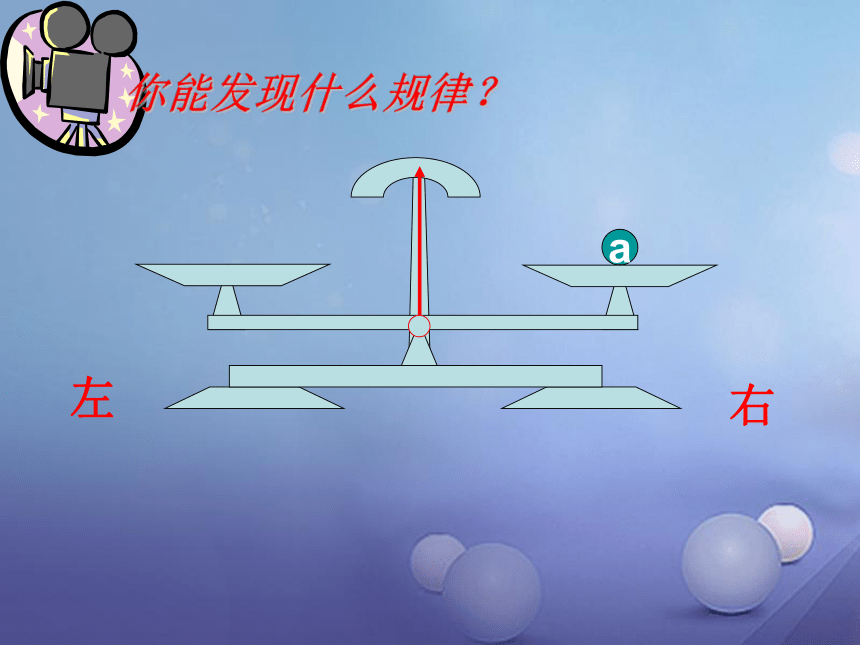
一、探索新知
a
右
左
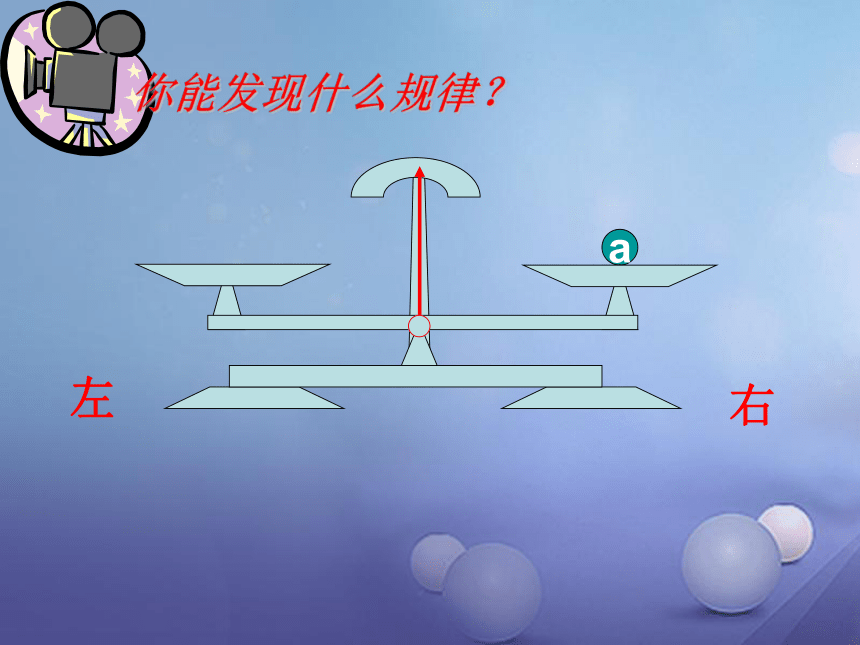
a
右
左
a
右
左
a
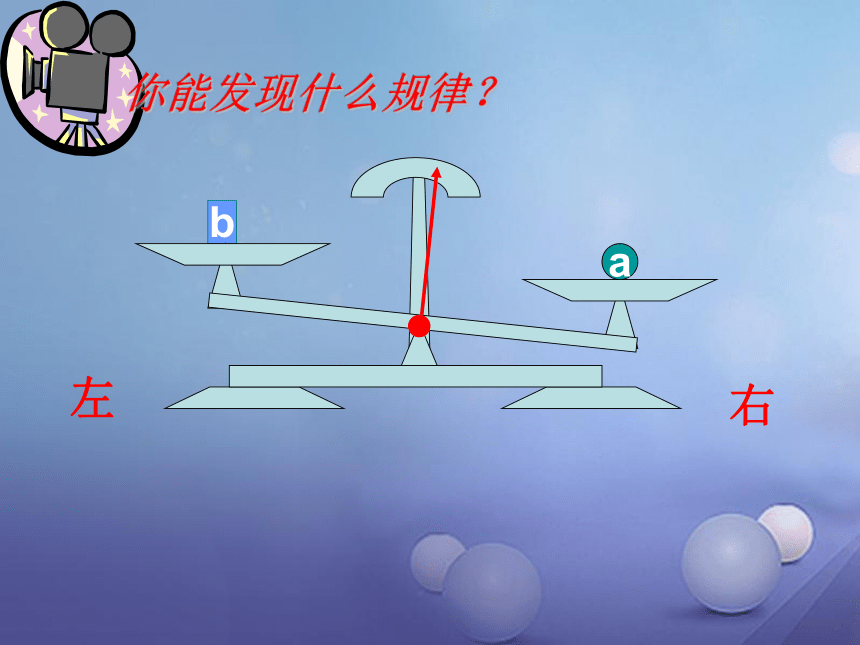
b
右
左
b
a
右
左
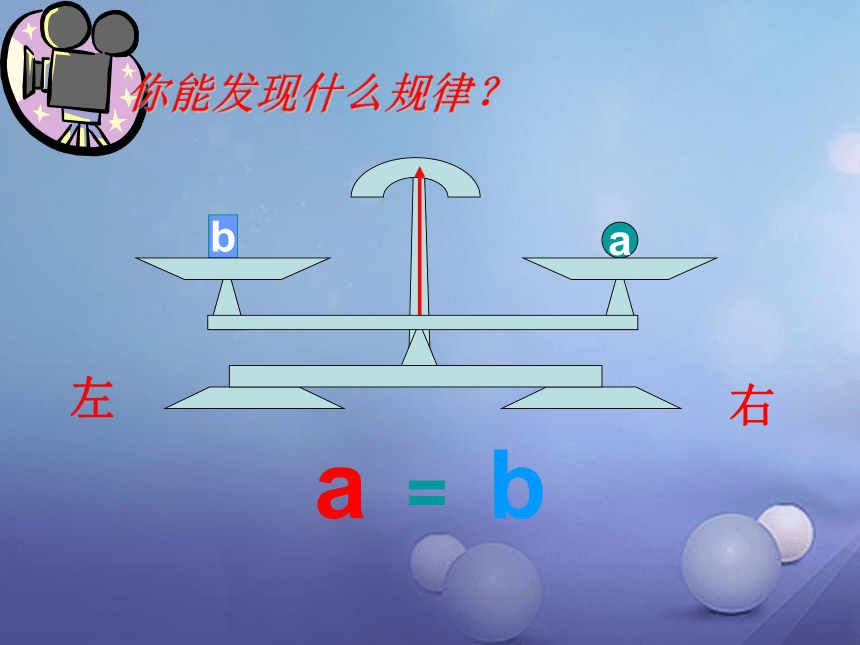
b
a
a = b
右
左
b
a
a = b
c
右
左
c
b
a
a = b
右
左
a
c
b
a = b
右
左
c
b
c
a
a = b
右
左
c
b
c
a
a = b
a+c b+c
=
右
左
c
c
a = b
右
左
c
a = b
右
左
c
a = b
右
左
a = b
右
左
a = b
a-c b-c
=
右
左
等式的性质1:等式的两边同时加(或减)同一个数(或式子),结果仍相等.
性质1用式子可表示为:如果a=b , 那么 a±c=b±c
在下面的括号内填上适当的数或者式子:
(1)因为:
所以:
(2)因为:
所以:
想一想、练一练
3 =2 -8
3 =2 -8-2
b
a
a = b
右
左
b
a
a = b
右
左
a
b
2a = 2b
b
a
a = b
右
左
b
b
a
a
3a = 3b
b
a
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
b
a
a = b
右
左
等式的性质2:等式的两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
性质2用式子可表示为:
如果a=b, 那么 ac=bc
如果a=b,那么
等式的性质
性质1: 等式两边同时加(或减)同一个数(或式子), 结果仍相等.
性质2: 等式两边同时乘同一个数, 或除以同一个不为0的数, 结果仍相等.
注意:(1)等式两边都要参加运算,且是同一种运算.
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能都除以0,即0不能作除数或分母.
二、应用新知
(1)如果x=y,那么??????????????? (????? )?????????
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )?
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
利用等式的性质解下列方程
解:两边减7,得
解:两边除以-5,得
分析:所谓“解方程”就是要求出方程的解“x=?”因此我们需要把方程转化为“x=a(a为常数)”的形式.
解:两边加5,得
两边同乘-3,得
检验:
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(1)如果 ,那么下列等式中不一定成立
的是( )
A.
C.
D.
B.
(2)解方程
2x-7=9
(3)解方程
5(y-1)=10.
等式的性质
掌握关键:<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
3.1.2 等式的性质
一、探索新知
a
右
左
a
右
左
a
右
左
a
b
右
左
b
a
右
左
b
a
a = b
右
左
b
a
a = b
c
右
左
c
b
a
a = b
右
左
a
c
b
a = b
右
左
c
b
c
a
a = b
右
左
c
b
c
a
a = b
a+c b+c
=
右
左
c
c
a = b
右
左
c
a = b
右
左
c
a = b
右
左
a = b
右
左
a = b
a-c b-c
=
右
左
等式的性质1:等式的两边同时加(或减)同一个数(或式子),结果仍相等.
性质1用式子可表示为:如果a=b , 那么 a±c=b±c
在下面的括号内填上适当的数或者式子:
(1)因为:
所以:
(2)因为:
所以:
想一想、练一练
3 =2 -8
3 =2 -8-2
b
a
a = b
右
左
b
a
a = b
右
左
a
b
2a = 2b
b
a
a = b
右
左
b
b
a
a
3a = 3b
b
a
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
b
a
a = b
右
左
等式的性质2:等式的两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
性质2用式子可表示为:
如果a=b, 那么 ac=bc
如果a=b,那么
等式的性质
性质1: 等式两边同时加(或减)同一个数(或式子), 结果仍相等.
性质2: 等式两边同时乘同一个数, 或除以同一个不为0的数, 结果仍相等.
注意:(1)等式两边都要参加运算,且是同一种运算.
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能都除以0,即0不能作除数或分母.
二、应用新知
(1)如果x=y,那么??????????????? (????? )?????????
(2)如果x=y,那么??????????????????? (????? )
(3)如果x=y,那么??????????????????? (????? )
(4)如果x=y,那么??????????????????? (????? )
(5)如果x=y,那么??????????????????? (????? )?
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
利用等式的性质解下列方程
解:两边减7,得
解:两边除以-5,得
分析:所谓“解方程”就是要求出方程的解“x=?”因此我们需要把方程转化为“x=a(a为常数)”的形式.
解:两边加5,得
两边同乘-3,得
检验:
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(1)如果 ,那么下列等式中不一定成立
的是( )
A.
C.
D.
B.
(2)解方程
2x-7=9
(3)解方程
5(y-1)=10.
等式的性质
掌握关键:<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
