冀教版九年级数学上册第二十七章反比例函数分类训练(含答案)
文档属性
| 名称 | 冀教版九年级数学上册第二十七章反比例函数分类训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 453.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 00:00:00 | ||
图片预览

文档简介
第二十七章反比例函数
类型之一 反比例函数的定义及表达式的确定
1. 如图1,已知P是反比例函数y=(x>0)的图像上的一个动点,连接OP,若将线段OP绕点O逆时针旋转90°得到线段OQ,则经过点Q的双曲线的函数表达式为( )
A.y= B.y=-
C.y= D.y=-
图1
2.已知反比例函数y=(k≠0),当自变量x满足-2≤x≤-时,对应的函数值y满足≤y≤1,则k的值为( )
A.- B.- C.-2 D.-
3.已知反比例函数y=的图像经过点(-3,-1),则k=________.
4.已知M为反比例函数y=的图像上的一点,MA⊥y轴,垂足为A,△AMO的面积为2,则k的值为________.
5.某村利用秋冬季节兴修水利,计划请运输公司用90~150天(含90与150天)完成总量300万米3的土石方运送.设运输公司完成任务所需的时间为y(单位:天),平均每天运输土石方量为x(单位:万米3),请写出y关于x的函数表达式,并给出自变量x的取值范围:____________________.
类型之二 反比例函数的图像及性质
6.对于反比例函数y=-,下列说法不正确的是( )
A.图像分布在第二、四象限
B.当x>0时,y的值随x的值增大而增大
C.图像经过点(1,-2)
D.若点A(x1,y1),B(x2,y2)都在该函数图像上,且x1<x2,则y1<y2
7.已知点A(1,y1),B(3,y2),C(-8,y3)都在反比例函数y=的图像上,则y1,y2,y3的大小关系是( )
A.y3C.y28.若点P(-m2-1,m-3)在第三象限,则反比例函数y=的图像在第________象限.
类型之三 反比例函数与一次函数的综合
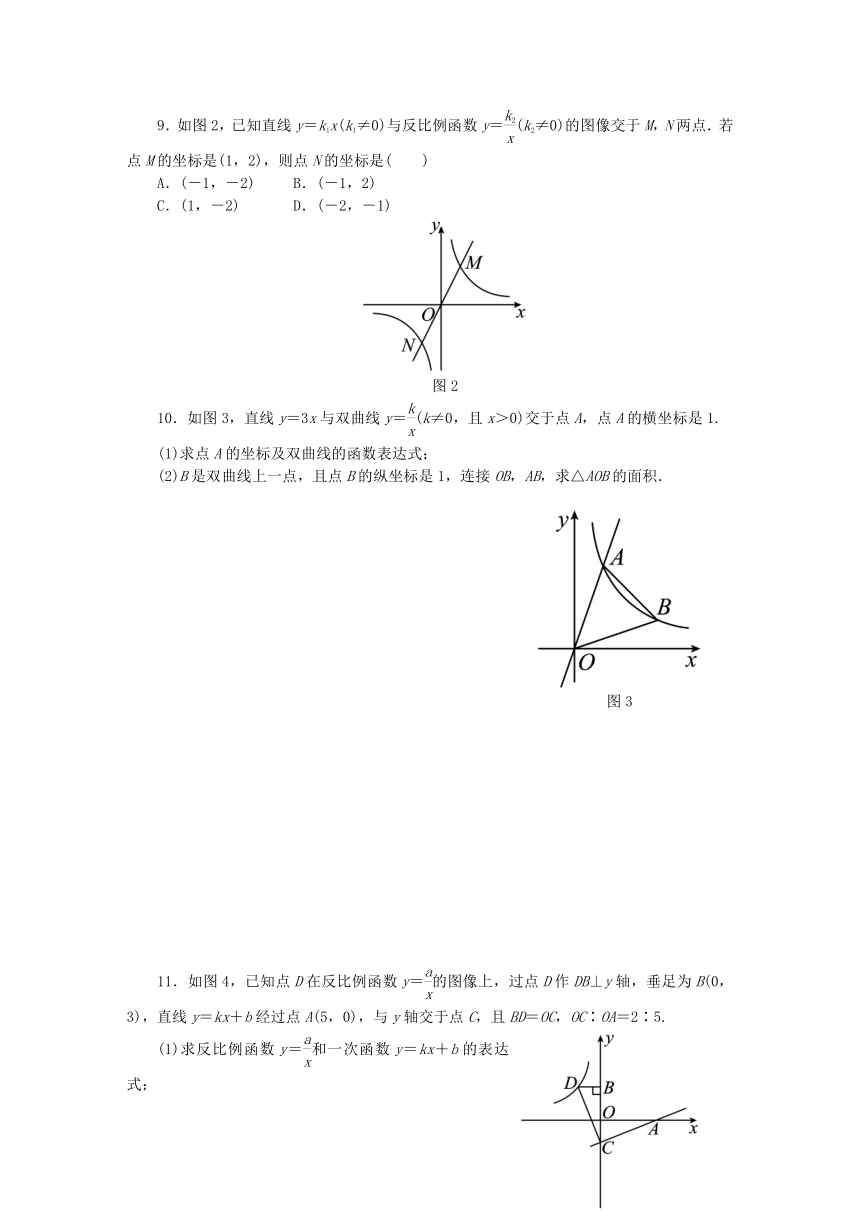
9.如图2,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图像交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
图2
10.如图3,直线y=3x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的函数表达式;
(2)B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
图3
11.如图4,已知点D在反比例函数y=的图像上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C,且BD=OC,OC∶OA=2∶5.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)求关于x的不等式>kx+b的解集.
图4
类型之四 反比例函数的应用
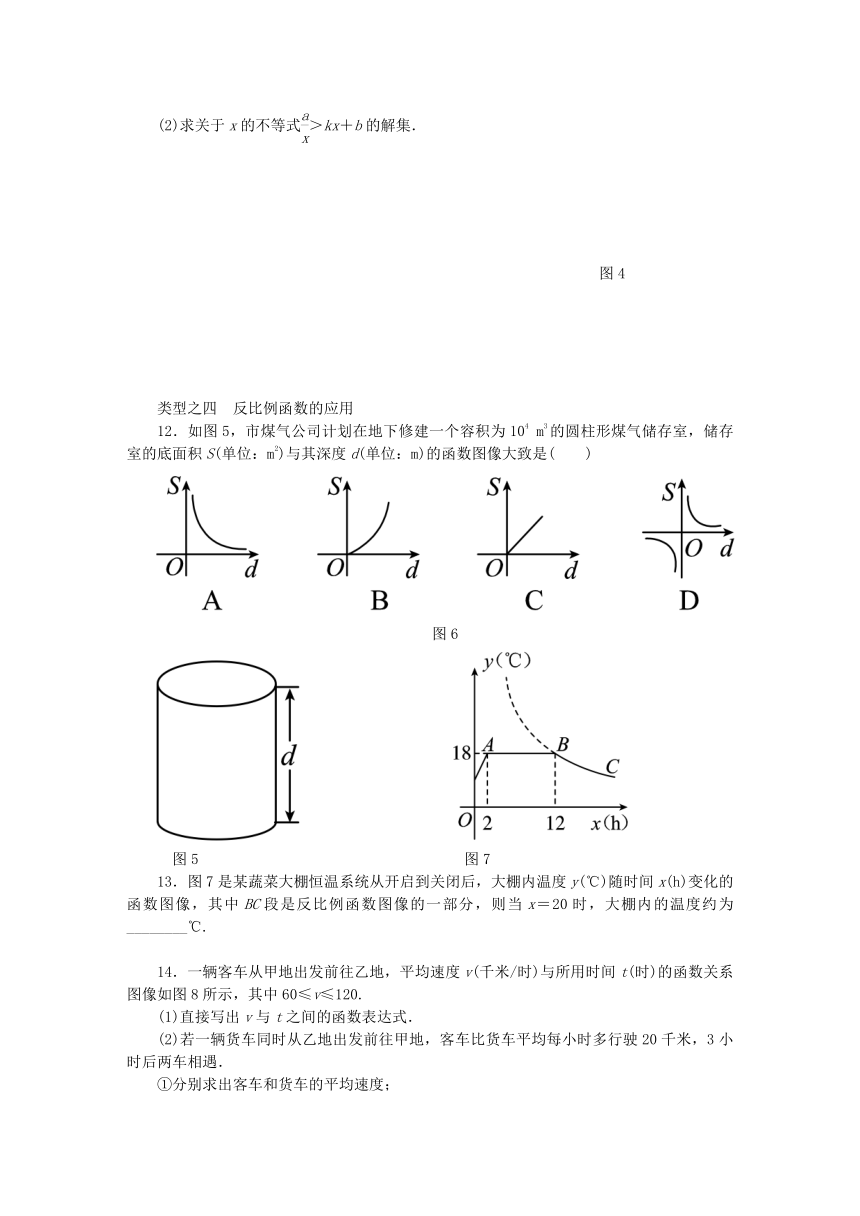
12.如图5,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图像大致是( )
图6
图5 图7
13.图7是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(h)变化的函数图像,其中BC段是反比例函数图像的一部分,则当x=20时,大棚内的温度约为________℃.
14.一辆客车从甲地出发前往乙地,平均速度v(千米/时)与所用时间t(时)的函数关系图像如图8所示,其中60≤v≤120.
(1)直接写出v与t之间的函数表达式.
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①分别求出客车和货车的平均速度;
②甲、乙两地间有两个加油站A,B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
图8
类型之五 数学活动
15.小明根据学习函数的经验,对函数y=x+的图像与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+的自变量x的取值范围是________.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=________,n=________;
x … -3 -2 -1 - - 1 2 3 4 …
y … - - -2 - - m 2 n …
(3)如图9,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图像;
(4)结合函数的图像,请完成:
①当y=-时,x=________;
②写出该函数的一条性质__________________;
③若方程x+=t有两个不相等的实数根,则t的取值范围是____________.
图9
答案
1.D 2.A 3.3
4.±4
5.y=(2≤x≤)
6.D
7.D
8.二、四
9.A .
10.解:(1)将x=1代入y=3x,得y=3,
∴点A的坐标为(1,3).
将A(1,3)代入y=,得k=3,
∴双曲线的函数表达式为y=.
(2)在y=中,令y=1,则x=3,∴B(3,1).
如图,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长CA,DB交于点E.
∵A(1,3),B(3,1),
∴OC=3,OD=3,AC=1,AE=2,
BE=2,BD=1,
∴S△AOB=S矩形OCED-S△AOC-S△BOD-S△ABE=3×3-×1×3-×1×3-×2×2=4.
11.解:(1)∵BD=OC,OC∶OA=2∶5,点A(5,0),点B(0,3),
∴OA=5,OC=BD=2,OB=3.
又∵点C在y轴负半轴,点D在第二象限,
∴点C的坐标为(0,-2),点D的坐标为(-2,3).
∵点D(-2,3)在反比例函数y=的图像上,∴a=-2×3=-6,
∴反比例函数的表达式为y=-.
将A(5,0),C(0,-2)代入y=kx+b,
得
解得
∴一次函数的表达式为y=x-2.
(2)将y=x-2代入y=-,
整理,得x2-2x+6=0.
∵b2-4ac=(-2)2-4××6=-<0,
∴一次函数图像与反比例函数图像无交点.
观察下图图像可知当x<0时,反比例函数图像在一次函数图像上方,
∴不等式>kx+b的解集为x<0.
12.A .
13.10.8
14.解:(1)v=(5≤t≤10).
(2)①依题意,得3(v+v-20)=600,解得v=110.经检验,v=110符合题意.
当v=110时,v-20=110-20=90(千米/时).
答:客车与货车的平均速度分别为110千米/时和90千米/时.
②若A加油站在甲地和B加油站之间,110t-(600-90t)=200,
解得t=4,此时110t=110×4=440(千米);
若B加油站在甲地和A加油站之间,110t+200+90t=600,
解得t=2,此时110t=110×2=220(千米).
答:甲地与B加油站的距离为220千米或440千米.
15.解:(1)x≠0
(2)当x=时,y=x+=;
当x=3时,y=x+=.故答案为,.
(3)连点成线,画出函数图像如下:
(4)①-4或-
②答案不唯一,如函数图像在第一、三象限且关于原点对称.
③t<-2或t>2
类型之一 反比例函数的定义及表达式的确定
1. 如图1,已知P是反比例函数y=(x>0)的图像上的一个动点,连接OP,若将线段OP绕点O逆时针旋转90°得到线段OQ,则经过点Q的双曲线的函数表达式为( )
A.y= B.y=-
C.y= D.y=-
图1
2.已知反比例函数y=(k≠0),当自变量x满足-2≤x≤-时,对应的函数值y满足≤y≤1,则k的值为( )
A.- B.- C.-2 D.-
3.已知反比例函数y=的图像经过点(-3,-1),则k=________.
4.已知M为反比例函数y=的图像上的一点,MA⊥y轴,垂足为A,△AMO的面积为2,则k的值为________.
5.某村利用秋冬季节兴修水利,计划请运输公司用90~150天(含90与150天)完成总量300万米3的土石方运送.设运输公司完成任务所需的时间为y(单位:天),平均每天运输土石方量为x(单位:万米3),请写出y关于x的函数表达式,并给出自变量x的取值范围:____________________.
类型之二 反比例函数的图像及性质
6.对于反比例函数y=-,下列说法不正确的是( )
A.图像分布在第二、四象限
B.当x>0时,y的值随x的值增大而增大
C.图像经过点(1,-2)
D.若点A(x1,y1),B(x2,y2)都在该函数图像上,且x1<x2,则y1<y2
7.已知点A(1,y1),B(3,y2),C(-8,y3)都在反比例函数y=的图像上,则y1,y2,y3的大小关系是( )
A.y3
类型之三 反比例函数与一次函数的综合
9.如图2,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图像交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
图2
10.如图3,直线y=3x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的函数表达式;
(2)B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
图3
11.如图4,已知点D在反比例函数y=的图像上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C,且BD=OC,OC∶OA=2∶5.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)求关于x的不等式>kx+b的解集.
图4
类型之四 反比例函数的应用
12.如图5,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图像大致是( )
图6
图5 图7
13.图7是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(h)变化的函数图像,其中BC段是反比例函数图像的一部分,则当x=20时,大棚内的温度约为________℃.
14.一辆客车从甲地出发前往乙地,平均速度v(千米/时)与所用时间t(时)的函数关系图像如图8所示,其中60≤v≤120.
(1)直接写出v与t之间的函数表达式.
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①分别求出客车和货车的平均速度;
②甲、乙两地间有两个加油站A,B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
图8
类型之五 数学活动
15.小明根据学习函数的经验,对函数y=x+的图像与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+的自变量x的取值范围是________.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=________,n=________;
x … -3 -2 -1 - - 1 2 3 4 …
y … - - -2 - - m 2 n …
(3)如图9,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图像;
(4)结合函数的图像,请完成:
①当y=-时,x=________;
②写出该函数的一条性质__________________;
③若方程x+=t有两个不相等的实数根,则t的取值范围是____________.
图9
答案
1.D 2.A 3.3
4.±4
5.y=(2≤x≤)
6.D
7.D
8.二、四
9.A .
10.解:(1)将x=1代入y=3x,得y=3,
∴点A的坐标为(1,3).
将A(1,3)代入y=,得k=3,
∴双曲线的函数表达式为y=.
(2)在y=中,令y=1,则x=3,∴B(3,1).
如图,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长CA,DB交于点E.
∵A(1,3),B(3,1),
∴OC=3,OD=3,AC=1,AE=2,
BE=2,BD=1,
∴S△AOB=S矩形OCED-S△AOC-S△BOD-S△ABE=3×3-×1×3-×1×3-×2×2=4.
11.解:(1)∵BD=OC,OC∶OA=2∶5,点A(5,0),点B(0,3),
∴OA=5,OC=BD=2,OB=3.
又∵点C在y轴负半轴,点D在第二象限,
∴点C的坐标为(0,-2),点D的坐标为(-2,3).
∵点D(-2,3)在反比例函数y=的图像上,∴a=-2×3=-6,
∴反比例函数的表达式为y=-.
将A(5,0),C(0,-2)代入y=kx+b,
得
解得
∴一次函数的表达式为y=x-2.
(2)将y=x-2代入y=-,
整理,得x2-2x+6=0.
∵b2-4ac=(-2)2-4××6=-<0,
∴一次函数图像与反比例函数图像无交点.
观察下图图像可知当x<0时,反比例函数图像在一次函数图像上方,
∴不等式>kx+b的解集为x<0.
12.A .
13.10.8
14.解:(1)v=(5≤t≤10).
(2)①依题意,得3(v+v-20)=600,解得v=110.经检验,v=110符合题意.
当v=110时,v-20=110-20=90(千米/时).
答:客车与货车的平均速度分别为110千米/时和90千米/时.
②若A加油站在甲地和B加油站之间,110t-(600-90t)=200,
解得t=4,此时110t=110×4=440(千米);
若B加油站在甲地和A加油站之间,110t+200+90t=600,
解得t=2,此时110t=110×2=220(千米).
答:甲地与B加油站的距离为220千米或440千米.
15.解:(1)x≠0
(2)当x=时,y=x+=;
当x=3时,y=x+=.故答案为,.
(3)连点成线,画出函数图像如下:
(4)①-4或-
②答案不唯一,如函数图像在第一、三象限且关于原点对称.
③t<-2或t>2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
