人教版九年级数学上册22.3实际问题与二次函数——何时获得最大利润课件 (共23张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数——何时获得最大利润课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 21:51:10 | ||
图片预览






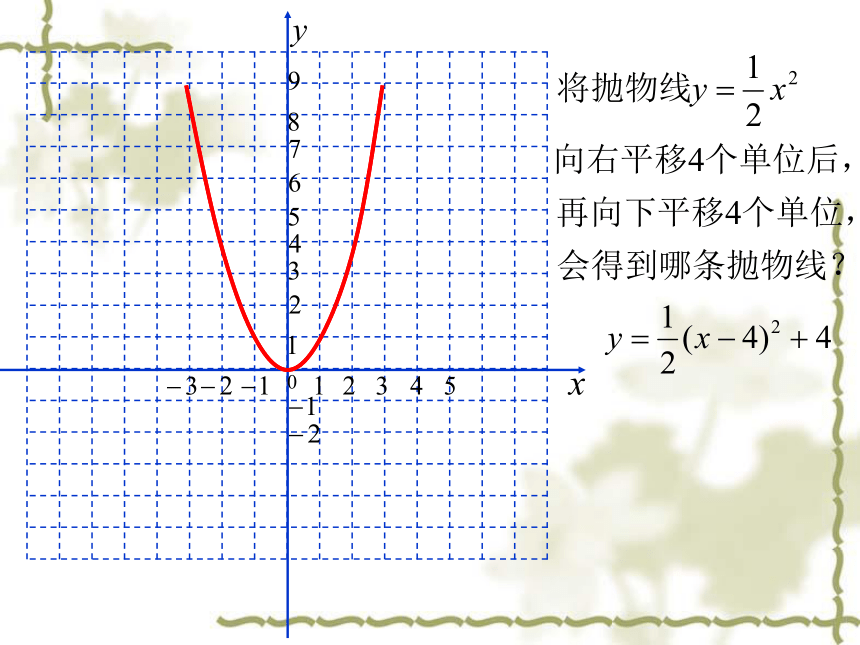

文档简介
(共23张PPT)
22.3实际问题与二次函数(1)
主要内容:本节内容是如何用二次函数解决现实生活中的实际问题,或如何用二次函数解释现实世界中的一些现象.主要涉及以下三个现实世界中运用二次函数的问题:
探究1.最大利润问题;
2.磁盘储存量问题;
3.水位问题。
课时安排:
第一课时 探究1.最大利润问题;
第二课时 探究 2.磁盘储存量问题;
第三课时 探究 3.水位问题。
教学目标
知识技能:进一步运用二次函数的概念解决实际问题。
数学思考:在运用二次函数解决实际问题中的最大利润问
题的过程中,进一步体会数学建模思想,培养
学生的数学应用意识。
解决问题:经历“实际问题—建立模型—拓展应用”的过
程,发展学生分析问题、解决问题的能力。
情感态度:运用二次函数解决实际问题的过程中,体验
数学的实用性,提高学习数学的兴趣。
教学重难点
教学重点:运用二次函数的意义和性质解决实际
问题。
教学难点:运用二次函数的思想方法分析解决实
际问题,在解决实际问题的过程中进一
步巩固二次函数的性质。
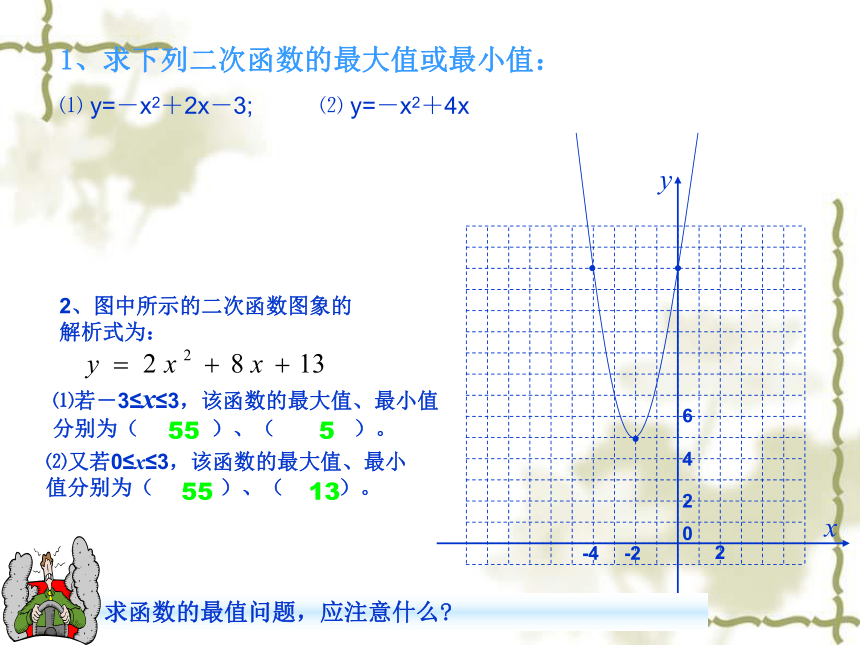
55 5
55 13
2、图中所示的二次函数图象的解析式为:
1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x-3; ⑵ y=-x2+4x
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是
自变量?哪些量随之发生了变化?
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
(0≤X≤30)
(0≤X≤30)
所以,当定价为65元时,利润最大,最大利润为6250元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
何时橙子总产量最大
某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
何时橙子总产量最大
果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子,因此果园橙子的总产量
你能根据表格中的数据作出猜想吗?
y=(100+x)(600-5x)=-5x?+100x+60000.
在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?
X/棵 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Y/个
2.利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系?
何时橙子总产量最大
1.利用函数关系式描述橙子的总产量与增种橙子树的棵数之间的关系.
3.增种多少棵橙子,可以使橙子的总产量在60400个以上?
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
∵篮圈中心距离地面3米
∴此球不能投中
若假设出手的角度和力度都不变,
则如何才能使此球命中?
(1)跳得高一点
(2)向前平移一点
(4,4)
(8,3)
在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?
0 1 2 3 4 5 6 7 8 9
(8,3)
(5,4)
(4,4)
0 1 2 3 4 5 6 7 8 9
在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
(7,3)●
用抛物线的知识解决运动场上或者生活中的一些实际问题的一般步骤:
建立直角坐标系
二次函数
问题求解
找出实际问题的答案
生活是数学的源泉,探索是数学的生命线.
寄语
作业
习题22.3 第 2、3、4
22.3实际问题与二次函数(1)
主要内容:本节内容是如何用二次函数解决现实生活中的实际问题,或如何用二次函数解释现实世界中的一些现象.主要涉及以下三个现实世界中运用二次函数的问题:
探究1.最大利润问题;
2.磁盘储存量问题;
3.水位问题。
课时安排:
第一课时 探究1.最大利润问题;
第二课时 探究 2.磁盘储存量问题;
第三课时 探究 3.水位问题。
教学目标
知识技能:进一步运用二次函数的概念解决实际问题。
数学思考:在运用二次函数解决实际问题中的最大利润问
题的过程中,进一步体会数学建模思想,培养
学生的数学应用意识。
解决问题:经历“实际问题—建立模型—拓展应用”的过
程,发展学生分析问题、解决问题的能力。
情感态度:运用二次函数解决实际问题的过程中,体验
数学的实用性,提高学习数学的兴趣。
教学重难点
教学重点:运用二次函数的意义和性质解决实际
问题。
教学难点:运用二次函数的思想方法分析解决实
际问题,在解决实际问题的过程中进一
步巩固二次函数的性质。
55 5
55 13
2、图中所示的二次函数图象的解析式为:
1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x-3; ⑵ y=-x2+4x
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是
自变量?哪些量随之发生了变化?
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
(0≤X≤30)
(0≤X≤30)
所以,当定价为65元时,利润最大,最大利润为6250元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
何时橙子总产量最大
某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
何时橙子总产量最大
果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子,因此果园橙子的总产量
你能根据表格中的数据作出猜想吗?
y=(100+x)(600-5x)=-5x?+100x+60000.
在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?
X/棵 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Y/个
2.利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系?
何时橙子总产量最大
1.利用函数关系式描述橙子的总产量与增种橙子树的棵数之间的关系.
3.增种多少棵橙子,可以使橙子的总产量在60400个以上?
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
∵篮圈中心距离地面3米
∴此球不能投中
若假设出手的角度和力度都不变,
则如何才能使此球命中?
(1)跳得高一点
(2)向前平移一点
(4,4)
(8,3)
在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?
0 1 2 3 4 5 6 7 8 9
(8,3)
(5,4)
(4,4)
0 1 2 3 4 5 6 7 8 9
在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
(7,3)●
用抛物线的知识解决运动场上或者生活中的一些实际问题的一般步骤:
建立直角坐标系
二次函数
问题求解
找出实际问题的答案
生活是数学的源泉,探索是数学的生命线.
寄语
作业
习题22.3 第 2、3、4
同课章节目录
