安徽省合肥市阳光中学2019-2020学年第一学期九年级数学12月份月考试卷(PDF版,含答案)
文档属性
| 名称 | 安徽省合肥市阳光中学2019-2020学年第一学期九年级数学12月份月考试卷(PDF版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 716.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 17:10:12 | ||
图片预览

文档简介
书
考试时间:120分钟 满分:150分
一、选择题:(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符
合题意的,请在答题卷上将正确答案的字母代号涂黑)
1?抛物线y=x2-3x+2与y轴交点的坐标是
A?(0,2) B?(1,0) C?(0,-3) D?(0,0)
2?cos30°=
A?12 B?
槡3
2 槡C?3 D?
槡3
3
3?观察下列每组图形,相似图形是
A? B? C? D?
4?若反比例函数y=kx图象经过点(5,-1),该函数图象在
A?第一、二象限 B?第一、三象限
C?第二、三象限 D?第二、四象限
5?对于二次函数y=-14x
2+x-4,下列说法正确的是
A?当x>0时,y随x的增大而增大 B?当x=2时,y有最大值-3
C?图象的顶点坐标为(-2,-7) D?图象与x轴有两个交点
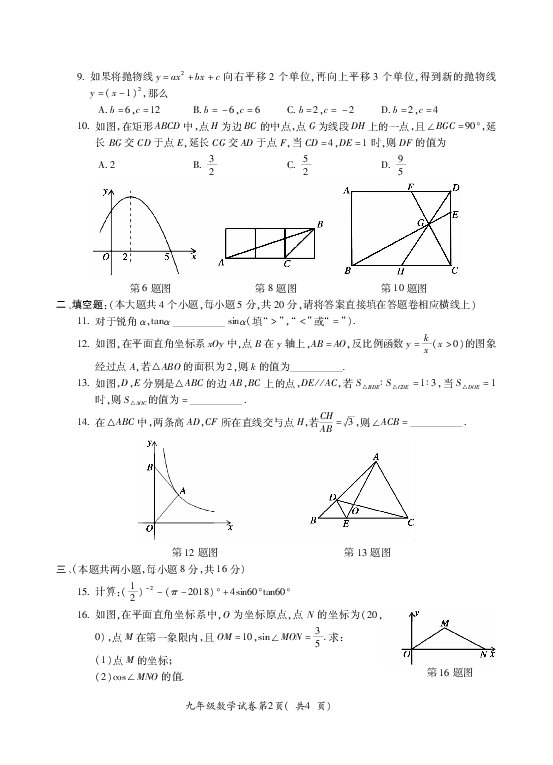
6?如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是
A?x<-1 B?x>5
C?-1<x<5 D?x<-1或x>5
7?若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相
比
A?增加了10% B?减少了10% C?增加了(1+10%) D?没有改变
8?如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是
A? B? C? D?
合肥市阳光中学2019-2020学年度月考测试
九年级数学(沪科版)
九年级数学试卷第1页(共4页)
9?如果将抛物线y=ax2+bx+c向右平移2个单位,再向上平移3个单位,得到新的抛物线
y=(x-1)2,那么
A?b=6,c=12 B?b=-6,c=6 C?b=2,c=-2 D?b=2,c=4
10?如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上的一点,且∠BGC=90°,延
长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的值为
A?2 B?32 C?
5
2 D?
9
5
第6题图 第8题图 第10题图
二、填空题:(本大题共4个小题,每小题5分,共20分,请将答案直接填在答题卷相应横线上)
11?对于锐角α,tanα sinα(填“>”,“<”或“=”)?
12?如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=kx(x>0)的图象
经过点A,若△ABO的面积为2,则k的值为 .
13?如图,D,E分别是△ABC的边 AB,BC上的点,DE//AC,若 S△BDE∶S△CDE=1∶3,当 S△DOE=1
时,则S△AOC的值为= ?
14?在△ABC中,两条高AD,CF所在直线交与点H,若CHAB 槡=3,则∠ACB= ?
第12题图 第13题图
三、(本题共两小题,每小题8分,共16分)
15?计算:(12)
-2-(π-2018)°+4sin60°tan60°
第16题图
16?如图,在平面直角坐标系中,O为坐标原点,点 N的坐标为(20,
0),点M在第一象限内,且OM=10,sin∠MON=35.求:
(1)点M的坐标;
(2)cos∠MNO的值.
九年级数学试卷第2页(共4页)
四、(本题共两小题,每小题8分,共16分)
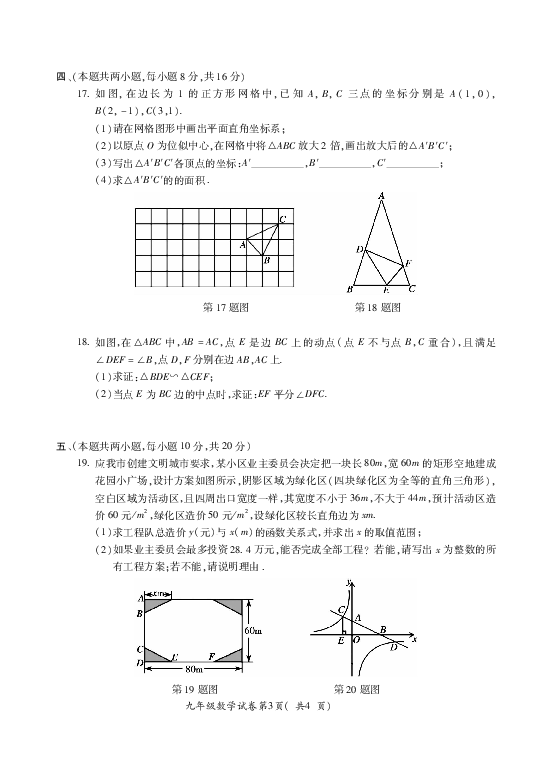
17?如图,在边长为 1的正方形网格中,已知 A,B,C三点的坐标分别是 A(1,0),
B(2,-1),C(3,1).
(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,在网格中将△ABC放大2倍,画出放大后的△A′B′C′;
(3)写出△A′B′C′各顶点的坐标:A′ ,B′ ,C′ ;
(4)求△A′B′C′的的面积?
第17题图 第18题图
18?如图,在△ABC中,AB=AC,点 E是边 BC上的动点(点 E不与点 B,C重合),且满足
∠DEF=∠B,点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E为BC边的中点时,求证:EF平分∠DFC.
五、(本题共两小题,每小题10分,共20分)
19?应我市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成
花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),
空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造
价60元/m2,绿化区造价50元/m2,设绿化区较长直角边为xm?
(1)求工程队总造价y(元)与x(m)的函数关系式,并求出x的取值范围;
(2)如果业主委员会最多投资28?4万元,能否完成全部工程?若能,请写出x为整数的所
有工程方案;若不能,请说明理由?
第19题图 第20题图
九年级数学试卷第3页(共4页)
20?已知:如图,在平面直角坐标系xOy中,直线AB分别与 x轴,y轴交于点 B,A,与反比例函
数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO=12,OB=4,OE=2.
(1)求该反比例函数的解析式;
(2)求△CDE的面积.
六、(本题满分12分)
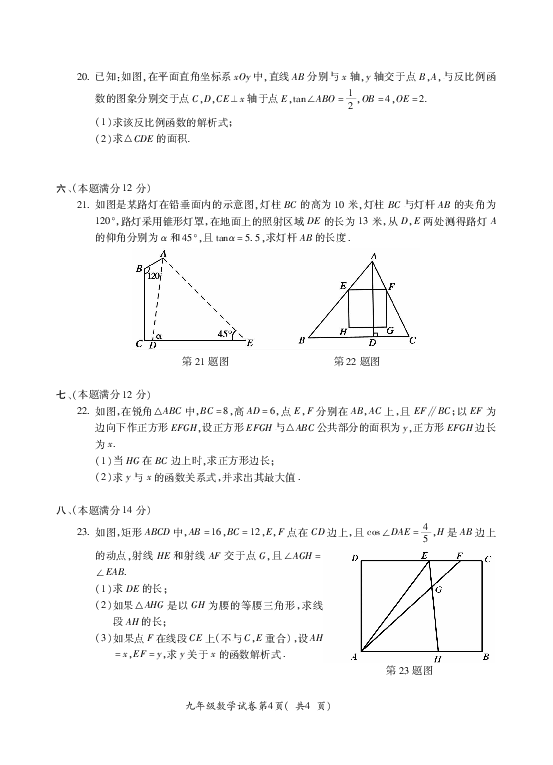
21?如图是某路灯在铅垂面内的示意图,灯柱 BC的高为10米,灯柱 BC与灯杆 AB的夹角为
120°,路灯采用锥形灯罩,在地面上的照射区域 DE的长为13米,从 D,E两处测得路灯 A
的仰角分别为α和45°,且tanα=5?5,求灯杆AB的长度?
第21题图 第22题图
七、(本题满分12分)
22?如图,在锐角△ABC中,BC=8,高AD=6,点 E,F分别在 AB,AC上,且 EF∥BC;以 EF为
边向下作正方形EFGH,设正方形EFGH与△ABC公共部分的面积为y,正方形EFGH边长
为x?
(1)当HG在BC边上时,求正方形边长;
(2)求y与x的函数关系式,并求出其最大值?
八、(本题满分14分)
23?如图,矩形ABCD中,AB=16,BC=12,E,F点在CD边上,且cos∠DAE=45,H是AB边上
第23题图
的动点,射线 HE和射线 AF交于点 G,且∠AGH=
∠EAB?
(1)求DE的长;
(2)如果△AHG是以 GH为腰的等腰三角形,求线
段AH的长;
(3)如果点F在线段CE上(不与C,E重合),设AH
=x,EF=y,求y关于x的函数解析式?
九年级数学试卷第4页(共4页)
九年级数学参考答案和评分标准(沪科版)
一、选择题:(本大题共10小题,每小题4分,共40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A B C D B C D A C A
二、填空题:(本大题共4个小题,每小题5分,共20分)
11?> 12?2 13?16 14?30°或150°
三、本题共两小题,每小题8分,共16分
15?解:原式=4-1+4×槡32 槡×3 4分……………………………………………………………
=3+6=9 8分………………………………………………………………………
16?解:(1)过点M作MP⊥ON,垂足为点P,由sin∠MON=MPCM得MD=6,
从而OP=8,故点M的坐标是(8,6); 4分…………………………………………
(2)由(1)知MP=6,PN=20-8=12,∴MN= 62+12槡
2
槡=65
∴cos∠MNO=MPMN=
12
槡65
= 槡255. 8分…………………………………………………
四、本题共两小题,每小题8分共16分
17?解:(1)(2)
3分…………………………………………………
(3)从图可知:A(-2,0),B(-4,2),C(-6,-2); 6分…………………………………
(4)S△A′B′C′=6(过程略). 8分……………………………………………………………
18?证明:(1)∵AB=AC,∴∠B=∠C,
∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,
∵∠DEF=∠B,∴∠BDE=∠CEF,∴△BDE∽△CEF; 4分……………………
(2)∵△BDE∽△CEF,∴BECF=
DE
EF,
九年级数学参考答案及评分标准第1页(共4页)
∵点E是BC的中点,∴BE=CE,∴CECF=
DE
EF,
∵∠DEF=∠B=∠C,∴△DEF∽△ECF,
∴∠DFE=∠CFE,∴FE平分∠DFC. 8分………………………………………
19?(本题满分10分)
解:(1)由题意得:BC=EF=80-2x,∴AB=CD=60-(80-2x)2 =x-10, 2分…………
y=50×4×12x(x-10)+60[60×80-4×
1
2x(x-10)]
=-20x2+200x+288000, 4分………………………………………………………
∵36≤80-2x≤44,∴18≤x≤22. 6分………………………………………………
(2)∵y=-20x2+200x+288000≤284000,∴x≤-10或x≥20, 8分…………………
∵18≤x≤22,∴20≤x≤22.
∴业主委员会最多投资28?4万元,能完成全部工程。
所有工程方案如下: 9分………………………………………………………………
①较长直角边为20m,短直角边为10m,出口宽度为40m;
②较长直角边为21m,短直角边为11m,出口宽度为38m;
③较长直角边为22m,短直角边为12m,出口宽度为36m. 12分…………………
20?(本题满分10分)
解:(1)∵tan∠ABO=12,OB=4,∴OA=2,
∵OE=2,∴BE=6,
∴CE=BE·tan∠ABO=3. 即点C的坐标为(-2,3), 3分………………………
∴反比例函数的解析式为:y=-6x; 5分……………………………………………
(2)设直线AB的解析式为:y=kx+b,则
4k+b=0,
b=2{ , 解得
k=-12,
b=2{ .
则直线AB的解析式为:y=-12x+2, 7分…………………………………………
由
y=-12x+2,
y=-6x
{ , 解得 x=-2,y=3{ , 或 x=6,y=-1{ .
∴点D的坐标为(6,-1), 9分………………………………………………………
∴△CDE的面积=12. 10分…………………………………………………………
九年级数学参考答案及评分标准第2页(共4页)
21?(本题满分12分)
解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠E=45°.
设AF=x.∵AF⊥CE, ∠E=45°,
∴EF=AF=x. 2分…………………………………………………………………………
∵在Rt△ADF中,tan∠ADF=AFDF,∠ADE=α
∴DF= AFtan∠ADF
= xtanα
=x5?5=
2x
11, 4分…………………………………………………
∵DE=13,
∴x+2x11=13, 解得x=11 6分………………………………………………………
∴AG=AF-GF=11-10=1 7分…………………………………………………………
∵∠ABC=120°,∠ABC=120°
∴∠ABG=∠ABC-∠CBG=120°-90°=30°. 9分……………………………………
∴AB=2AG=2
答:灯杆AB的长度为2米. 12分?……………………………………………………………
22?(本题满分12分)
解:(1)设EF与AD交于点K
∵EF∥BC ∴△AEF∽△ABC ∴AKAD=
EF
BC ∴AK=
3
4x 2分……………
当HG在BC边上时,DK=x ∴AK=AD-KD=6-x
∴34x=6-x ∴x=
24
7
即当HG在BC边上时,正方形边长为247 4分………………………………………
(2)当0<x≤247时,y=x
2 6分……………………………………………………………
当
24
7<x≤8时,DK=AD-AK=6-
3
4x
∴y=x(6-34x)=-
3
4x
2+6x
∴y=
x2 (0<x≤247)
y=-34x
2+6x (247<x≤6
{ ) 8分……………………………………………
当0<x≤247时,x=
24
7,y有最大值为
576
49; 9分………………………………………
九年级数学参考答案及评分标准第3页(共4页)
当
24
7<x≤6时,x=4,y有最大值为12. 11分………………………………………
∵12>57649
∴当x=4时,y有最大值为12. 12分………………………………………………
23?(本题满分14分)
解:(1)∵cos∠DAE=ADAE=
4
5,∴AE=15
∵AD=12,∴DE=9. 3分……………………………………………………………
(2)当GH=AH时,则∠AGH=∠GAH,
∵∠AGH=∠EAB,∴∠GAH=∠EAB,
∴G点与E点重合,即EH=HA,
作HM⊥AE于M,如图1,则AM=12AE=
15
2,
易证∠DAE=∠AHM,∴sin∠AHM=sin∠DAE,
即
AM
AH=
DE
AE=
9
15=
3
5 ∴AH=
25
2 6分………………………………………………
当GA=GH时,则∠GAH=∠GHA,
∵∠AGH=∠EAB,
∴∠AEH=180°-∠EAB-∠AHE=180°-∠AGH-∠AHG=∠GAH=∠GHA
∴AH=AE=15, 9分……………………………………………………………………
综上所述,线段AH的长为252或15; 10分……………………………………………
(3)设EG=a,HG=b
易证△AHG∽△EHA,∴AH2=HG·EH即x2=b(a+b)
由△EFG∽△HAG得EFAH=
EG
GH,即
y
x=
a
b
∴x+yx =
a+b
b,∴x
2·
x+y
x =b(a+b)·
a+b
b
即x(x+y)=(a+b)2=EH2=(x-9)2+122=x2-18x+225
∴y=225-18xx . 14分…………………………………………………………………
(其它解法请根据以上评分标准酌情赋分)
九年级数学参考答案及评分标准第4页(共4页)
考试时间:120分钟 满分:150分
一、选择题:(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符
合题意的,请在答题卷上将正确答案的字母代号涂黑)
1?抛物线y=x2-3x+2与y轴交点的坐标是
A?(0,2) B?(1,0) C?(0,-3) D?(0,0)
2?cos30°=
A?12 B?
槡3
2 槡C?3 D?
槡3
3
3?观察下列每组图形,相似图形是
A? B? C? D?
4?若反比例函数y=kx图象经过点(5,-1),该函数图象在
A?第一、二象限 B?第一、三象限
C?第二、三象限 D?第二、四象限
5?对于二次函数y=-14x
2+x-4,下列说法正确的是
A?当x>0时,y随x的增大而增大 B?当x=2时,y有最大值-3
C?图象的顶点坐标为(-2,-7) D?图象与x轴有两个交点
6?如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是
A?x<-1 B?x>5
C?-1<x<5 D?x<-1或x>5
7?若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相
比
A?增加了10% B?减少了10% C?增加了(1+10%) D?没有改变
8?如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是
A? B? C? D?
合肥市阳光中学2019-2020学年度月考测试
九年级数学(沪科版)
九年级数学试卷第1页(共4页)
9?如果将抛物线y=ax2+bx+c向右平移2个单位,再向上平移3个单位,得到新的抛物线
y=(x-1)2,那么
A?b=6,c=12 B?b=-6,c=6 C?b=2,c=-2 D?b=2,c=4
10?如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上的一点,且∠BGC=90°,延
长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的值为
A?2 B?32 C?
5
2 D?
9
5
第6题图 第8题图 第10题图
二、填空题:(本大题共4个小题,每小题5分,共20分,请将答案直接填在答题卷相应横线上)
11?对于锐角α,tanα sinα(填“>”,“<”或“=”)?
12?如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=kx(x>0)的图象
经过点A,若△ABO的面积为2,则k的值为 .
13?如图,D,E分别是△ABC的边 AB,BC上的点,DE//AC,若 S△BDE∶S△CDE=1∶3,当 S△DOE=1
时,则S△AOC的值为= ?
14?在△ABC中,两条高AD,CF所在直线交与点H,若CHAB 槡=3,则∠ACB= ?
第12题图 第13题图
三、(本题共两小题,每小题8分,共16分)
15?计算:(12)
-2-(π-2018)°+4sin60°tan60°
第16题图
16?如图,在平面直角坐标系中,O为坐标原点,点 N的坐标为(20,
0),点M在第一象限内,且OM=10,sin∠MON=35.求:
(1)点M的坐标;
(2)cos∠MNO的值.
九年级数学试卷第2页(共4页)
四、(本题共两小题,每小题8分,共16分)
17?如图,在边长为 1的正方形网格中,已知 A,B,C三点的坐标分别是 A(1,0),
B(2,-1),C(3,1).
(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,在网格中将△ABC放大2倍,画出放大后的△A′B′C′;
(3)写出△A′B′C′各顶点的坐标:A′ ,B′ ,C′ ;
(4)求△A′B′C′的的面积?
第17题图 第18题图
18?如图,在△ABC中,AB=AC,点 E是边 BC上的动点(点 E不与点 B,C重合),且满足
∠DEF=∠B,点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E为BC边的中点时,求证:EF平分∠DFC.
五、(本题共两小题,每小题10分,共20分)
19?应我市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成
花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),
空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造
价60元/m2,绿化区造价50元/m2,设绿化区较长直角边为xm?
(1)求工程队总造价y(元)与x(m)的函数关系式,并求出x的取值范围;
(2)如果业主委员会最多投资28?4万元,能否完成全部工程?若能,请写出x为整数的所
有工程方案;若不能,请说明理由?
第19题图 第20题图
九年级数学试卷第3页(共4页)
20?已知:如图,在平面直角坐标系xOy中,直线AB分别与 x轴,y轴交于点 B,A,与反比例函
数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO=12,OB=4,OE=2.
(1)求该反比例函数的解析式;
(2)求△CDE的面积.
六、(本题满分12分)
21?如图是某路灯在铅垂面内的示意图,灯柱 BC的高为10米,灯柱 BC与灯杆 AB的夹角为
120°,路灯采用锥形灯罩,在地面上的照射区域 DE的长为13米,从 D,E两处测得路灯 A
的仰角分别为α和45°,且tanα=5?5,求灯杆AB的长度?
第21题图 第22题图
七、(本题满分12分)
22?如图,在锐角△ABC中,BC=8,高AD=6,点 E,F分别在 AB,AC上,且 EF∥BC;以 EF为
边向下作正方形EFGH,设正方形EFGH与△ABC公共部分的面积为y,正方形EFGH边长
为x?
(1)当HG在BC边上时,求正方形边长;
(2)求y与x的函数关系式,并求出其最大值?
八、(本题满分14分)
23?如图,矩形ABCD中,AB=16,BC=12,E,F点在CD边上,且cos∠DAE=45,H是AB边上
第23题图
的动点,射线 HE和射线 AF交于点 G,且∠AGH=
∠EAB?
(1)求DE的长;
(2)如果△AHG是以 GH为腰的等腰三角形,求线
段AH的长;
(3)如果点F在线段CE上(不与C,E重合),设AH
=x,EF=y,求y关于x的函数解析式?
九年级数学试卷第4页(共4页)
九年级数学参考答案和评分标准(沪科版)
一、选择题:(本大题共10小题,每小题4分,共40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A B C D B C D A C A
二、填空题:(本大题共4个小题,每小题5分,共20分)
11?> 12?2 13?16 14?30°或150°
三、本题共两小题,每小题8分,共16分
15?解:原式=4-1+4×槡32 槡×3 4分……………………………………………………………
=3+6=9 8分………………………………………………………………………
16?解:(1)过点M作MP⊥ON,垂足为点P,由sin∠MON=MPCM得MD=6,
从而OP=8,故点M的坐标是(8,6); 4分…………………………………………
(2)由(1)知MP=6,PN=20-8=12,∴MN= 62+12槡
2
槡=65
∴cos∠MNO=MPMN=
12
槡65
= 槡255. 8分…………………………………………………
四、本题共两小题,每小题8分共16分
17?解:(1)(2)
3分…………………………………………………
(3)从图可知:A(-2,0),B(-4,2),C(-6,-2); 6分…………………………………
(4)S△A′B′C′=6(过程略). 8分……………………………………………………………
18?证明:(1)∵AB=AC,∴∠B=∠C,
∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,
∵∠DEF=∠B,∴∠BDE=∠CEF,∴△BDE∽△CEF; 4分……………………
(2)∵△BDE∽△CEF,∴BECF=
DE
EF,
九年级数学参考答案及评分标准第1页(共4页)
∵点E是BC的中点,∴BE=CE,∴CECF=
DE
EF,
∵∠DEF=∠B=∠C,∴△DEF∽△ECF,
∴∠DFE=∠CFE,∴FE平分∠DFC. 8分………………………………………
19?(本题满分10分)
解:(1)由题意得:BC=EF=80-2x,∴AB=CD=60-(80-2x)2 =x-10, 2分…………
y=50×4×12x(x-10)+60[60×80-4×
1
2x(x-10)]
=-20x2+200x+288000, 4分………………………………………………………
∵36≤80-2x≤44,∴18≤x≤22. 6分………………………………………………
(2)∵y=-20x2+200x+288000≤284000,∴x≤-10或x≥20, 8分…………………
∵18≤x≤22,∴20≤x≤22.
∴业主委员会最多投资28?4万元,能完成全部工程。
所有工程方案如下: 9分………………………………………………………………
①较长直角边为20m,短直角边为10m,出口宽度为40m;
②较长直角边为21m,短直角边为11m,出口宽度为38m;
③较长直角边为22m,短直角边为12m,出口宽度为36m. 12分…………………
20?(本题满分10分)
解:(1)∵tan∠ABO=12,OB=4,∴OA=2,
∵OE=2,∴BE=6,
∴CE=BE·tan∠ABO=3. 即点C的坐标为(-2,3), 3分………………………
∴反比例函数的解析式为:y=-6x; 5分……………………………………………
(2)设直线AB的解析式为:y=kx+b,则
4k+b=0,
b=2{ , 解得
k=-12,
b=2{ .
则直线AB的解析式为:y=-12x+2, 7分…………………………………………
由
y=-12x+2,
y=-6x
{ , 解得 x=-2,y=3{ , 或 x=6,y=-1{ .
∴点D的坐标为(6,-1), 9分………………………………………………………
∴△CDE的面积=12. 10分…………………………………………………………
九年级数学参考答案及评分标准第2页(共4页)
21?(本题满分12分)
解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠E=45°.
设AF=x.∵AF⊥CE, ∠E=45°,
∴EF=AF=x. 2分…………………………………………………………………………
∵在Rt△ADF中,tan∠ADF=AFDF,∠ADE=α
∴DF= AFtan∠ADF
= xtanα
=x5?5=
2x
11, 4分…………………………………………………
∵DE=13,
∴x+2x11=13, 解得x=11 6分………………………………………………………
∴AG=AF-GF=11-10=1 7分…………………………………………………………
∵∠ABC=120°,∠ABC=120°
∴∠ABG=∠ABC-∠CBG=120°-90°=30°. 9分……………………………………
∴AB=2AG=2
答:灯杆AB的长度为2米. 12分?……………………………………………………………
22?(本题满分12分)
解:(1)设EF与AD交于点K
∵EF∥BC ∴△AEF∽△ABC ∴AKAD=
EF
BC ∴AK=
3
4x 2分……………
当HG在BC边上时,DK=x ∴AK=AD-KD=6-x
∴34x=6-x ∴x=
24
7
即当HG在BC边上时,正方形边长为247 4分………………………………………
(2)当0<x≤247时,y=x
2 6分……………………………………………………………
当
24
7<x≤8时,DK=AD-AK=6-
3
4x
∴y=x(6-34x)=-
3
4x
2+6x
∴y=
x2 (0<x≤247)
y=-34x
2+6x (247<x≤6
{ ) 8分……………………………………………
当0<x≤247时,x=
24
7,y有最大值为
576
49; 9分………………………………………
九年级数学参考答案及评分标准第3页(共4页)
当
24
7<x≤6时,x=4,y有最大值为12. 11分………………………………………
∵12>57649
∴当x=4时,y有最大值为12. 12分………………………………………………
23?(本题满分14分)
解:(1)∵cos∠DAE=ADAE=
4
5,∴AE=15
∵AD=12,∴DE=9. 3分……………………………………………………………
(2)当GH=AH时,则∠AGH=∠GAH,
∵∠AGH=∠EAB,∴∠GAH=∠EAB,
∴G点与E点重合,即EH=HA,
作HM⊥AE于M,如图1,则AM=12AE=
15
2,
易证∠DAE=∠AHM,∴sin∠AHM=sin∠DAE,
即
AM
AH=
DE
AE=
9
15=
3
5 ∴AH=
25
2 6分………………………………………………
当GA=GH时,则∠GAH=∠GHA,
∵∠AGH=∠EAB,
∴∠AEH=180°-∠EAB-∠AHE=180°-∠AGH-∠AHG=∠GAH=∠GHA
∴AH=AE=15, 9分……………………………………………………………………
综上所述,线段AH的长为252或15; 10分……………………………………………
(3)设EG=a,HG=b
易证△AHG∽△EHA,∴AH2=HG·EH即x2=b(a+b)
由△EFG∽△HAG得EFAH=
EG
GH,即
y
x=
a
b
∴x+yx =
a+b
b,∴x
2·
x+y
x =b(a+b)·
a+b
b
即x(x+y)=(a+b)2=EH2=(x-9)2+122=x2-18x+225
∴y=225-18xx . 14分…………………………………………………………………
(其它解法请根据以上评分标准酌情赋分)
九年级数学参考答案及评分标准第4页(共4页)
同课章节目录
