山东省肥城市2019—2020学年度上学期期末教学质量检测八年级数学试题(解析版)
文档属性
| 名称 | 山东省肥城市2019—2020学年度上学期期末教学质量检测八年级数学试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 07:55:31 | ||
图片预览




文档简介
2019—2020学年度上学期期末教学质量检测
八年级数学试题
注意事项:
答题前请将答题纸上的考生信息填(涂)清楚,然后将试题答案认真填写(填涂)在答题纸的指定位置,否则答题无效。
本试卷共6页,考试时间120分钟,满分150分。
考试结束只交答题纸。
一、选择题(本大题共12小题,每题给出的四个选项中只有一个正确,请将正确答案的字母代号填涂在答题纸的指定位置,共48分)
如图,下列条件:,,,,中能判断直线的有
A. 5个 B. 4个 C. 3个 D. 2个
如图,?ABCD的对角线AC,BD交于点O,下列
结论不一定成立的是
A. B. C. D.
下列四个分式中,是最简分式的是
A. B. C. D.
已知等腰三角形一腰上的高线与另一腰的夹角为,那么这个等腰三角形的顶角等于? ?
A. 或 B. C. D. 或
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知,现添加以下的哪个条件仍不能判定≌
A. B. C. D.
第5题 第6题
如图所示,≌,≌,B,E,C在一条直线上.下列结论:是的平分线;;;线段DE是的中线;其中正确的有个.
A. 2 B. 3 C. 4 D. 5
若关于x的分式方程 有增根,则m的值是? ? ?
A.m=0或m=3 B. m=3 C. m=0 D. m=-1
如图,在中,,,DE是边AC的垂直平分线,连结AE,则等于
A. B. C. D.
第8题 第9题 第11题
如图,AD是的角平分线,,垂足为F,,和的面积分别为60和35,则的面积为
A. 25 B. C. D.
小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程
A. B. C. D.
如图,平行四边形ABCD的对角线交于点O,且,的周长为23,则平行四边形ABCD的两条对角线的和是
A. 18 B. 28 C. 36 D. 46
已知,则的值等于
A. 1 B. 0 C. D.
二、填空题(本大题共6小题,请将每题的答案填写在答题纸指定位置的横线上,共24分)
已知,则______.
如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分和,若,,则的周长是______.
第14题 第15题 第17题
如图,直线,,为直角,则______.
已知,则______.
如图,于E,于F,若,,则下列结论:;平分;;中正确的是______.
如图,在?ABCD中,对角线AC平分,MN与AC交于点O,M,N分别在AB,CD上,且,连接若,则的度数为______
三、计算题(请在答题纸的指定位置写出解题必须的过程)
(7分)(1)化简:.
(7分)解方程:.
(10分)先化简,再求值:,其中a满足方程.
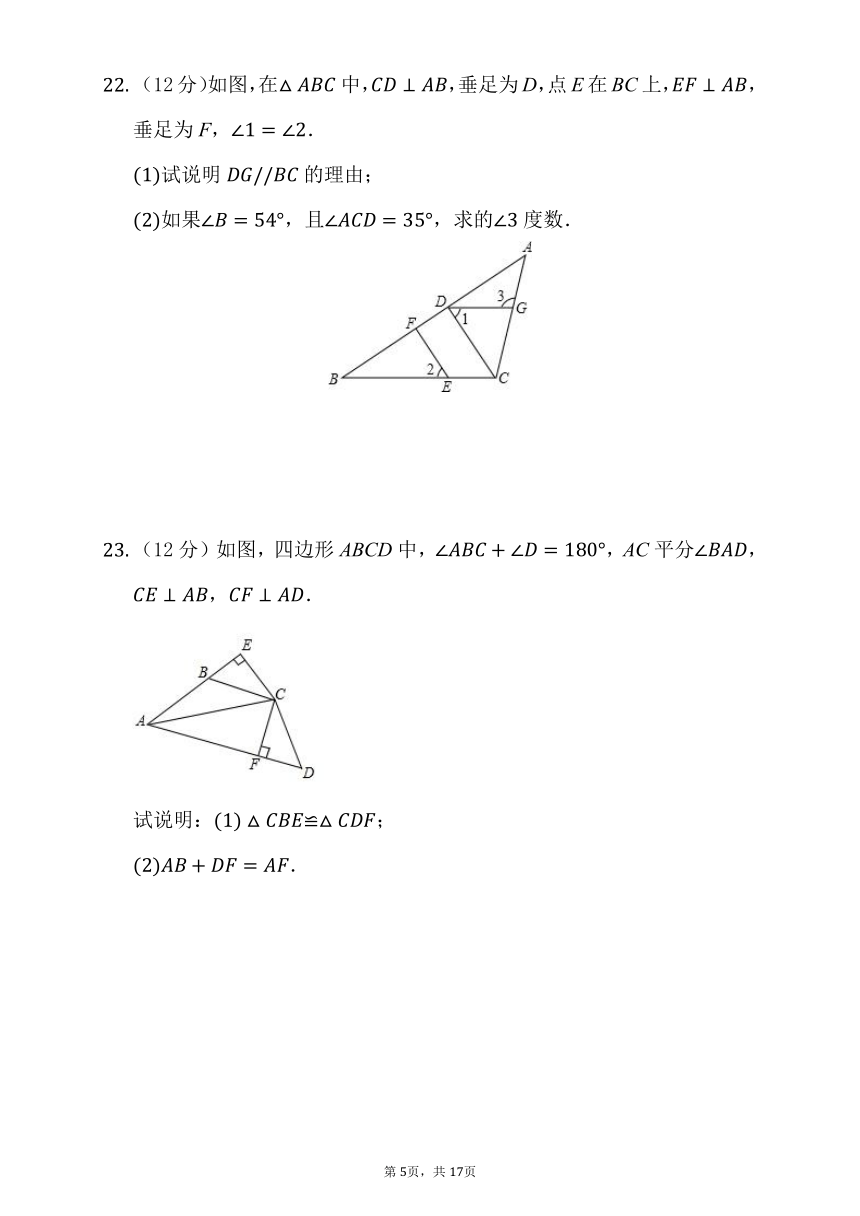
(12分)如图,在中,,垂足为D,点E在BC上,,垂足为F,.
试说明的理由;
如果,且,求的度数.
(12分)如图,四边形ABCD中,,AC平分,,.
试说明:≌;
.
(15分)一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
甲、乙两车单独完成任务分别需要多少天?
已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
(15分)在中,,,,且.
如图1,,,垂足分别为点E,F,求证:
如图2,如果,且两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
答案和解析
1.【答案】B
【解析】【分析】
本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
根据平行线的判定定理对各小题进行逐一判断即可.
【解答】
解:,,故本小题正确;
,,故本小题正确;
,,故本小题正确;
不能判定,故本小题错误;
,,,,故本小题正确.
故选B.
2.【答案】D
【解析】【分析】
此题主要考查了平行四边形的性质,关键是熟练掌握平行四边形的性质定理:边:平行四边形的对边相等.角:平行四边形的对角相等.对角线:平行四边形的对角线互相平分.根据平行四边形的对边相等,平行四边形的对角线互相平分可得答案.
【解答】
解:四边形ABCD是平行四边形,
,,,,
故A、B、C都成立,只有D不一定成立,
故选D.
3.【答案】A
【解析】【分析】
本题考查最简分式的概念,涉及因式分解,分式的基本性质,本题属于基础题型.分子分母没有公因式即可为最简分式.
【解答】
解:A.,最简分式;
B.原式,故B不是最简分式;
C.原式,故C不是最简分式;
D.原式,故D不是最简分式.
故选A.
4.【答案】D
【解析】【分析】
本题考查了等腰三角形的性质,解题关键在于分两种情况进行讨论,作出图形更形象直观分两种情况进行讨论:当三角形是锐角三角形时,利用直角三角形两锐角互余求解;当三角形是钝角三角形时,利用三角形的一个外角等于与它不相邻的两个内角的和求解.
【解答】
解:
如图1,三角形是锐角三角形时,
,
顶角;
如图2,三角形是钝角三角形时,
,
顶角,
综上所述,顶角等于或.
故选D.
5.【答案】D
【解析】【分析】
此题主要考查学生对全等三角形判定定理的理解和掌握,此类添加条件题,要求学生应熟练掌握全等三角形的判定定理欲使≌,已知,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.
【解答】
解:,为公共角,
A、如添加,利用ASA即可证明≌;
B、如添,利用SAS即可证明≌;
C、如添,等量关系可得,利用SAS即可证明≌;
D、如添,因为SSA,不能证明≌,所以此选项不能作为添加的条件.
故选D.
6.【答案】A
【解析】【分析】
本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.也考查了等腰三角形三线合一的性质,直角三角形两锐角互余的性质,难度适中根据全等三角形的对应角相等得出,即可判断;先由全等三角形的对应边相等得出,,再根据等腰三角形三线合一的性质得出,则,再根据全等三角形的对应角相等得出,但A、D、C可能不在同一直线上,即可判断;根据全等三角形的对应角相等得出,,从而可判断,但A、D、C可能不在同一直线上,即可判断;根据全等三角形的对应边相等得出,再根据三角形中线的定义即可判断;根据全等三角形的对应边相等得出,但A、D、C可能不在同一直线上,所以可能不等于AC.
【解答】
解:≌,
,
是的平分线,故正确;
≌,
,,
,
,
≌,
,
,
、D、C可能不在同一直线上
可能不垂直于AC,故不正确;
≌,≌,
,,
若A、D、C不在同一直线上,则,
,故不正确;
≌,
,
线段DE是的中线,故正确;
≌,
,
若A、D、C不在同一直线上,则,
,故不正确.
故选A.
7.【答案】D
【解析】【分析】
本题考查了分式方程的增根,增根确定后可按如下步骤进行:化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值分式方程去分母转化为整式方程,由分式方程有增根,得到,求出x的值,代入整式方程求出m的值即可.
【解答】
解:去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:,
解得:.
故选D.
8.【答案】C
【解析】【分析】
本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
根据三角形的内角和定理求出,根据线段垂直平分线的性质得到,求出,计算即可.
【解答】
解:,,
,
是边AC的垂直平分线,
,
,
,
故选C.
9.【答案】D
【解析】【分析】
本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.过点D作于H,根据角平分线上的点到角的两边距离相等可得,再利用“HL”证明和全等,和全等,然后根据全等三角形的面积相等列方程求解即可.
【解答】
解:如图,过点D作于H,
是的角平分线,,
,
在和中,
,
≌,
,
在和中,
≌,
,
和的面积分别为60和35,
,
.
故选D.
10.【答案】B
【解析】【分析】
本题考查了分式方程的应用.注意准确找到等量关系是关键.由设他上月买了x本笔记本,则这次买了本,然后可求得两次每本笔记本的价格,由等量关系:每本比上月便宜1元,即可得到方程.
【解答】
解:依题意得他上月买了x本笔记本,则这次买了本,
根据题意得:,
即:.
故选B.
11.【答案】C
【解析】解:四边形ABCD是平行四边形,
,
的周长为23,
,
,,
平行四边形ABCD的两条对角线的和,
故选:C.
由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形的基本性质:平行四边形两组对边分别平行;平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分.
12.【答案】C
【解析】解:由,得
?
,
则,,
.
故选:C.
把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
13.【答案】
【解析】【分析】
此题考查了比例的性质,关键是将变形为根据,可得,再根据比例的性质即可求解.
【解答】
解:,
,
,
.
故答案为.
14.【答案】24
【解析】解:四边形ABCD是平行四边形,
,,
,
又和BP分别平分和,
,
在中,;
平分,
,
,
是等腰三角形,
,
同理:,
即,
在中,,,
,
的周长;
故答案为:24.
根据平行四边形性质得出,,推出,求出,在中求出,由勾股定理求出BP,证出,,得出,即可求出答案.
本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.
15.【答案】
【解析】【分析】
本题考查了平行线的性质的应用,能正确作出辅助线是解此题的关键.过E作,求出,根据平行线的性质得出,,求出,即可求出答案.
【解答】
解:过E作,
,
,
,,
,为直角,
,,
,
故答案为.
16.【答案】7
【解析】解:已知等式整理得:,
可得,即,
解得:,,
则.
故答案为:7
已知等式左边通分并利用同分母分式的加法法则计算,再利用分式相等的条件求出A与B的值,代入原式计算即可得到结果.
此题考查了分式的加减法,以及分式相等的条件,熟练掌握运算法则是解本题的关键.
17.【答案】
【解析】解:在和中,
,
≌,
,故正确;
又,,
平分,故正确;
在和中,
,
≌,
,
,
,
即,故正确;
由垂线段最短可得,故错误,
综上所述,正确的是.
故答案为:.
利用“HL”证明和全等,根据全等三角形对应边相等可得,再根据到角的两边距离相等的点在角的平分线上判断出AD平分,然后利用“HL”证明和全等,根据全等三角形对应边相等可得,再根据图形表示出表示出AE、AF,再整理即可得到.
本题考查了全等三角形的判定与性质,到角的两边距离相等的点在角的平分线上,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
18.【答案】62
【解析】【分析】
本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.根据菱形的性质以及,利用ASA可得≌,可得,然后可得,继而可求得的度数.
【解答】
解:由题意可知,四边形ABCD为菱形,
,,
,,
在和中,
,
≌,
,
,
,
,
,
,
.
故答案为62.
19.【答案】解:原式.
【解析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.
20.【答案】解:方程两边都乘,得:
,
,
解得:.
经检验是原分式方程的根,
是原方程的解.
【解析】本题考查了分式方程的解法解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解解分式方程一定注意要代入最简公分母验根.需注意:分式方程里单独的一个数和字母也必须乘最简公分母.
由,故本题的最简公分母是,方程两边都乘最简公分母,可把分式方程转换为整式方程求解.
21.【答案】解:原式
,
,,
原式.
【解析】把原式括号里的第二项提取,然后把原式的各项分子分母都分解因式,找出括号里两项分母的最简公分母,利用分式的基本性质对括号里两项进行通分,然后利用同分母分式的减法运算法则:分母不变,只把分子相减,计算出结果,然后利用分式的除法法则:除以一个数等于乘以这个数的倒数,变形为乘法运算,约分后即可把原式化为最简分式,把a满足的方程变形后,代入原式化简后的式子中即可求出值.
此题考查了分式的混合运算,以及多项式的运算.分式的化简求值题,应先对原式的分子分母分解因式,在分式的化简运算中,要通观全局,弄清有哪些运算,然后观察能否用法则,定律,分解因式及公式来简化运算,同时注意运算的结果要化到最简,然后再代值计算.
22.【答案】证明:,,
,
.
又,
,
.
解:在中,,
,
.
又,
.
【解析】由,即可得出,从而得出,再根据即可得出,依据“内错角相等,两直线平行”即可证出;
在中,利用三角形内角和为即可算出度数,从而得出的度数,再根据即可得出,通过角的计算即可得出结论.
本题考查了平行线的判定与性质,解题的关键是:找出;找出本题属于基础题,难度不大,解决该题型题目时,根据相等或互补的角证出两直线平行是关键.
23.【答案】证明:平分,,,
,,
,,
,
在和中,
,
≌.
证明:在和中,
,
≌,
,
.
【解析】根据角平分线的性质可得到,根据补角的性质可得到,已知,,从而利用AAS即可判定≌.
已知,,则根据HL判定≌得,最后证得即可.
本题考查了全等三角形的判定和性质;证明线段相等往往通过三角形全等来证明,还要运用相等的线段进行等量代换,这是很重要的方法,注意掌握.
24.【答案】解:设甲车单独完成任务需要x天,则乙单独完成需要2x天,根据题意可得:
,
解得:,
经检验得,x是原方程的解,则,
即甲车单独完成需要15天,乙车单独完成需要30天;
设甲车每天租金为a元,乙车每天租金为b元,
则根据两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元可得:
,
解得:,
租甲乙两车需要费用为:65000元;
单独租甲车的费用为:元;
单独租乙车需要的费用为:元;
综上可得,单独租甲车租金最少.
【解析】设甲车单独完成任务需要x天,则乙单独完成需要2x天,根据题意所述等量关系可得出方程,解出即可;
结合的结论,分别计算出三种方案各自所需的费用,然后比较即可.
此题考查了分式方程的应用及二元一次方程组的知识,分别得出甲、乙单独需要的天数,及甲、乙车的租金是解答本题的关键.
25.【答案】证明:,,
,
,
,
,,
,
,,
;
解:线段AE,AF,AD之间的数量关系为:,理由如下:
连接BD,如图所示:
,,
是等边三角形,
,,
,
,
,
,
在与中,
≌,
,
,
.
【解析】由等腰三角形的性质和已知条件得出,再证出,由含30角的直角三角形的性质得出,,即可得出结论;
连接BD,证明是等边三角形,得出,,证出,得出,由ASA证明≌,得出,即可得出结论.
本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
第6页,共17页
第1页,共17页
八年级数学试题
注意事项:
答题前请将答题纸上的考生信息填(涂)清楚,然后将试题答案认真填写(填涂)在答题纸的指定位置,否则答题无效。
本试卷共6页,考试时间120分钟,满分150分。
考试结束只交答题纸。
一、选择题(本大题共12小题,每题给出的四个选项中只有一个正确,请将正确答案的字母代号填涂在答题纸的指定位置,共48分)
如图,下列条件:,,,,中能判断直线的有
A. 5个 B. 4个 C. 3个 D. 2个
如图,?ABCD的对角线AC,BD交于点O,下列
结论不一定成立的是
A. B. C. D.
下列四个分式中,是最简分式的是
A. B. C. D.
已知等腰三角形一腰上的高线与另一腰的夹角为,那么这个等腰三角形的顶角等于? ?
A. 或 B. C. D. 或
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知,现添加以下的哪个条件仍不能判定≌
A. B. C. D.
第5题 第6题
如图所示,≌,≌,B,E,C在一条直线上.下列结论:是的平分线;;;线段DE是的中线;其中正确的有个.
A. 2 B. 3 C. 4 D. 5
若关于x的分式方程 有增根,则m的值是? ? ?
A.m=0或m=3 B. m=3 C. m=0 D. m=-1
如图,在中,,,DE是边AC的垂直平分线,连结AE,则等于
A. B. C. D.
第8题 第9题 第11题
如图,AD是的角平分线,,垂足为F,,和的面积分别为60和35,则的面积为
A. 25 B. C. D.
小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程
A. B. C. D.
如图,平行四边形ABCD的对角线交于点O,且,的周长为23,则平行四边形ABCD的两条对角线的和是
A. 18 B. 28 C. 36 D. 46
已知,则的值等于
A. 1 B. 0 C. D.
二、填空题(本大题共6小题,请将每题的答案填写在答题纸指定位置的横线上,共24分)
已知,则______.
如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分和,若,,则的周长是______.
第14题 第15题 第17题
如图,直线,,为直角,则______.
已知,则______.
如图,于E,于F,若,,则下列结论:;平分;;中正确的是______.
如图,在?ABCD中,对角线AC平分,MN与AC交于点O,M,N分别在AB,CD上,且,连接若,则的度数为______
三、计算题(请在答题纸的指定位置写出解题必须的过程)
(7分)(1)化简:.
(7分)解方程:.
(10分)先化简,再求值:,其中a满足方程.
(12分)如图,在中,,垂足为D,点E在BC上,,垂足为F,.
试说明的理由;
如果,且,求的度数.
(12分)如图,四边形ABCD中,,AC平分,,.
试说明:≌;
.
(15分)一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
甲、乙两车单独完成任务分别需要多少天?
已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
(15分)在中,,,,且.
如图1,,,垂足分别为点E,F,求证:
如图2,如果,且两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
答案和解析
1.【答案】B
【解析】【分析】
本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
根据平行线的判定定理对各小题进行逐一判断即可.
【解答】
解:,,故本小题正确;
,,故本小题正确;
,,故本小题正确;
不能判定,故本小题错误;
,,,,故本小题正确.
故选B.
2.【答案】D
【解析】【分析】
此题主要考查了平行四边形的性质,关键是熟练掌握平行四边形的性质定理:边:平行四边形的对边相等.角:平行四边形的对角相等.对角线:平行四边形的对角线互相平分.根据平行四边形的对边相等,平行四边形的对角线互相平分可得答案.
【解答】
解:四边形ABCD是平行四边形,
,,,,
故A、B、C都成立,只有D不一定成立,
故选D.
3.【答案】A
【解析】【分析】
本题考查最简分式的概念,涉及因式分解,分式的基本性质,本题属于基础题型.分子分母没有公因式即可为最简分式.
【解答】
解:A.,最简分式;
B.原式,故B不是最简分式;
C.原式,故C不是最简分式;
D.原式,故D不是最简分式.
故选A.
4.【答案】D
【解析】【分析】
本题考查了等腰三角形的性质,解题关键在于分两种情况进行讨论,作出图形更形象直观分两种情况进行讨论:当三角形是锐角三角形时,利用直角三角形两锐角互余求解;当三角形是钝角三角形时,利用三角形的一个外角等于与它不相邻的两个内角的和求解.
【解答】
解:
如图1,三角形是锐角三角形时,
,
顶角;
如图2,三角形是钝角三角形时,
,
顶角,
综上所述,顶角等于或.
故选D.
5.【答案】D
【解析】【分析】
此题主要考查学生对全等三角形判定定理的理解和掌握,此类添加条件题,要求学生应熟练掌握全等三角形的判定定理欲使≌,已知,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.
【解答】
解:,为公共角,
A、如添加,利用ASA即可证明≌;
B、如添,利用SAS即可证明≌;
C、如添,等量关系可得,利用SAS即可证明≌;
D、如添,因为SSA,不能证明≌,所以此选项不能作为添加的条件.
故选D.
6.【答案】A
【解析】【分析】
本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.也考查了等腰三角形三线合一的性质,直角三角形两锐角互余的性质,难度适中根据全等三角形的对应角相等得出,即可判断;先由全等三角形的对应边相等得出,,再根据等腰三角形三线合一的性质得出,则,再根据全等三角形的对应角相等得出,但A、D、C可能不在同一直线上,即可判断;根据全等三角形的对应角相等得出,,从而可判断,但A、D、C可能不在同一直线上,即可判断;根据全等三角形的对应边相等得出,再根据三角形中线的定义即可判断;根据全等三角形的对应边相等得出,但A、D、C可能不在同一直线上,所以可能不等于AC.
【解答】
解:≌,
,
是的平分线,故正确;
≌,
,,
,
,
≌,
,
,
、D、C可能不在同一直线上
可能不垂直于AC,故不正确;
≌,≌,
,,
若A、D、C不在同一直线上,则,
,故不正确;
≌,
,
线段DE是的中线,故正确;
≌,
,
若A、D、C不在同一直线上,则,
,故不正确.
故选A.
7.【答案】D
【解析】【分析】
本题考查了分式方程的增根,增根确定后可按如下步骤进行:化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值分式方程去分母转化为整式方程,由分式方程有增根,得到,求出x的值,代入整式方程求出m的值即可.
【解答】
解:去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:,
解得:.
故选D.
8.【答案】C
【解析】【分析】
本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
根据三角形的内角和定理求出,根据线段垂直平分线的性质得到,求出,计算即可.
【解答】
解:,,
,
是边AC的垂直平分线,
,
,
,
故选C.
9.【答案】D
【解析】【分析】
本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.过点D作于H,根据角平分线上的点到角的两边距离相等可得,再利用“HL”证明和全等,和全等,然后根据全等三角形的面积相等列方程求解即可.
【解答】
解:如图,过点D作于H,
是的角平分线,,
,
在和中,
,
≌,
,
在和中,
≌,
,
和的面积分别为60和35,
,
.
故选D.
10.【答案】B
【解析】【分析】
本题考查了分式方程的应用.注意准确找到等量关系是关键.由设他上月买了x本笔记本,则这次买了本,然后可求得两次每本笔记本的价格,由等量关系:每本比上月便宜1元,即可得到方程.
【解答】
解:依题意得他上月买了x本笔记本,则这次买了本,
根据题意得:,
即:.
故选B.
11.【答案】C
【解析】解:四边形ABCD是平行四边形,
,
的周长为23,
,
,,
平行四边形ABCD的两条对角线的和,
故选:C.
由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形的基本性质:平行四边形两组对边分别平行;平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分.
12.【答案】C
【解析】解:由,得
?
,
则,,
.
故选:C.
把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
13.【答案】
【解析】【分析】
此题考查了比例的性质,关键是将变形为根据,可得,再根据比例的性质即可求解.
【解答】
解:,
,
,
.
故答案为.
14.【答案】24
【解析】解:四边形ABCD是平行四边形,
,,
,
又和BP分别平分和,
,
在中,;
平分,
,
,
是等腰三角形,
,
同理:,
即,
在中,,,
,
的周长;
故答案为:24.
根据平行四边形性质得出,,推出,求出,在中求出,由勾股定理求出BP,证出,,得出,即可求出答案.
本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.
15.【答案】
【解析】【分析】
本题考查了平行线的性质的应用,能正确作出辅助线是解此题的关键.过E作,求出,根据平行线的性质得出,,求出,即可求出答案.
【解答】
解:过E作,
,
,
,,
,为直角,
,,
,
故答案为.
16.【答案】7
【解析】解:已知等式整理得:,
可得,即,
解得:,,
则.
故答案为:7
已知等式左边通分并利用同分母分式的加法法则计算,再利用分式相等的条件求出A与B的值,代入原式计算即可得到结果.
此题考查了分式的加减法,以及分式相等的条件,熟练掌握运算法则是解本题的关键.
17.【答案】
【解析】解:在和中,
,
≌,
,故正确;
又,,
平分,故正确;
在和中,
,
≌,
,
,
,
即,故正确;
由垂线段最短可得,故错误,
综上所述,正确的是.
故答案为:.
利用“HL”证明和全等,根据全等三角形对应边相等可得,再根据到角的两边距离相等的点在角的平分线上判断出AD平分,然后利用“HL”证明和全等,根据全等三角形对应边相等可得,再根据图形表示出表示出AE、AF,再整理即可得到.
本题考查了全等三角形的判定与性质,到角的两边距离相等的点在角的平分线上,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
18.【答案】62
【解析】【分析】
本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.根据菱形的性质以及,利用ASA可得≌,可得,然后可得,继而可求得的度数.
【解答】
解:由题意可知,四边形ABCD为菱形,
,,
,,
在和中,
,
≌,
,
,
,
,
,
,
.
故答案为62.
19.【答案】解:原式.
【解析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.
20.【答案】解:方程两边都乘,得:
,
,
解得:.
经检验是原分式方程的根,
是原方程的解.
【解析】本题考查了分式方程的解法解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解解分式方程一定注意要代入最简公分母验根.需注意:分式方程里单独的一个数和字母也必须乘最简公分母.
由,故本题的最简公分母是,方程两边都乘最简公分母,可把分式方程转换为整式方程求解.
21.【答案】解:原式
,
,,
原式.
【解析】把原式括号里的第二项提取,然后把原式的各项分子分母都分解因式,找出括号里两项分母的最简公分母,利用分式的基本性质对括号里两项进行通分,然后利用同分母分式的减法运算法则:分母不变,只把分子相减,计算出结果,然后利用分式的除法法则:除以一个数等于乘以这个数的倒数,变形为乘法运算,约分后即可把原式化为最简分式,把a满足的方程变形后,代入原式化简后的式子中即可求出值.
此题考查了分式的混合运算,以及多项式的运算.分式的化简求值题,应先对原式的分子分母分解因式,在分式的化简运算中,要通观全局,弄清有哪些运算,然后观察能否用法则,定律,分解因式及公式来简化运算,同时注意运算的结果要化到最简,然后再代值计算.
22.【答案】证明:,,
,
.
又,
,
.
解:在中,,
,
.
又,
.
【解析】由,即可得出,从而得出,再根据即可得出,依据“内错角相等,两直线平行”即可证出;
在中,利用三角形内角和为即可算出度数,从而得出的度数,再根据即可得出,通过角的计算即可得出结论.
本题考查了平行线的判定与性质,解题的关键是:找出;找出本题属于基础题,难度不大,解决该题型题目时,根据相等或互补的角证出两直线平行是关键.
23.【答案】证明:平分,,,
,,
,,
,
在和中,
,
≌.
证明:在和中,
,
≌,
,
.
【解析】根据角平分线的性质可得到,根据补角的性质可得到,已知,,从而利用AAS即可判定≌.
已知,,则根据HL判定≌得,最后证得即可.
本题考查了全等三角形的判定和性质;证明线段相等往往通过三角形全等来证明,还要运用相等的线段进行等量代换,这是很重要的方法,注意掌握.
24.【答案】解:设甲车单独完成任务需要x天,则乙单独完成需要2x天,根据题意可得:
,
解得:,
经检验得,x是原方程的解,则,
即甲车单独完成需要15天,乙车单独完成需要30天;
设甲车每天租金为a元,乙车每天租金为b元,
则根据两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元可得:
,
解得:,
租甲乙两车需要费用为:65000元;
单独租甲车的费用为:元;
单独租乙车需要的费用为:元;
综上可得,单独租甲车租金最少.
【解析】设甲车单独完成任务需要x天,则乙单独完成需要2x天,根据题意所述等量关系可得出方程,解出即可;
结合的结论,分别计算出三种方案各自所需的费用,然后比较即可.
此题考查了分式方程的应用及二元一次方程组的知识,分别得出甲、乙单独需要的天数,及甲、乙车的租金是解答本题的关键.
25.【答案】证明:,,
,
,
,
,,
,
,,
;
解:线段AE,AF,AD之间的数量关系为:,理由如下:
连接BD,如图所示:
,,
是等边三角形,
,,
,
,
,
,
在与中,
≌,
,
,
.
【解析】由等腰三角形的性质和已知条件得出,再证出,由含30角的直角三角形的性质得出,,即可得出结论;
连接BD,证明是等边三角形,得出,,证出,得出,由ASA证明≌,得出,即可得出结论.
本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
第6页,共17页
第1页,共17页
同课章节目录
