人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):38【基础】点、直线、圆与圆的位置关系(附答案)
文档属性
| 名称 | 人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):38【基础】点、直线、圆与圆的位置关系(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 22:50:14 | ||
图片预览



文档简介
点、直线、圆与圆的位置关系—知识讲解(基础)
【学习目标】
1. 理解点与圆的位置关系由点到圆心的距离决定;会画三角形的外接圆,熟识相关概念.
2. 理解直线与圆的各种位置关系, 会用点到直线的距离来判断直线与圆的位置关系; 3.了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交,圆心距等概念.理解两圆的位
置关系与d、r1、r2等量关系的等价条件并灵活应用它们解题.
【要点梳理】
要点一、点和圆的位置关系 1.点和圆的三种位置关系:
由于平面上圆的存在,就把平面上的点分成了三个集合,即圆内的点,圆上的点和圆外的点,这三类点各具有相同的性质和判定方法;设⊙O的半径为r,点P到圆心的距离为d,则有 / / / /
2.三角形的外接圆
经过三角形的三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心. 三角形的外心到三角形三个顶点的距离相等.
要点诠释:
(1)点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系;
(2)不在同一直线上的三个点确定一个圆. 要点二、直线和圆的位置关系
1.直线和圆的三种位置关系: (1) 相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线. (2) 相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点. (3) 相离:直线和圆没有公共点时,叫做直线和圆相离. 2.直线与圆的位置关系的判定和性质. 直线与圆的位置关系能否像点与圆的位置关系一样通过一些条件来进行分析判断呢? 由于圆心确定圆的位置,半径确定圆的大小,因此研究直线和圆的位置关系,就可以转化为直线和点(圆心)的位置关系.下面图(1)中直线与圆心的距离小于半径;图(2)中直线与圆心的距离等于半径;图(3)中直线与圆心的距离大于半径. / 如果⊙O的半径为r,圆心O到直线/的距离为d,那么 /
要点诠释: 这三个命题从左边到右边反映了直线与圆的位置关系所具有的性质;从右边到左边则是直线与圆的位置关系的判定.
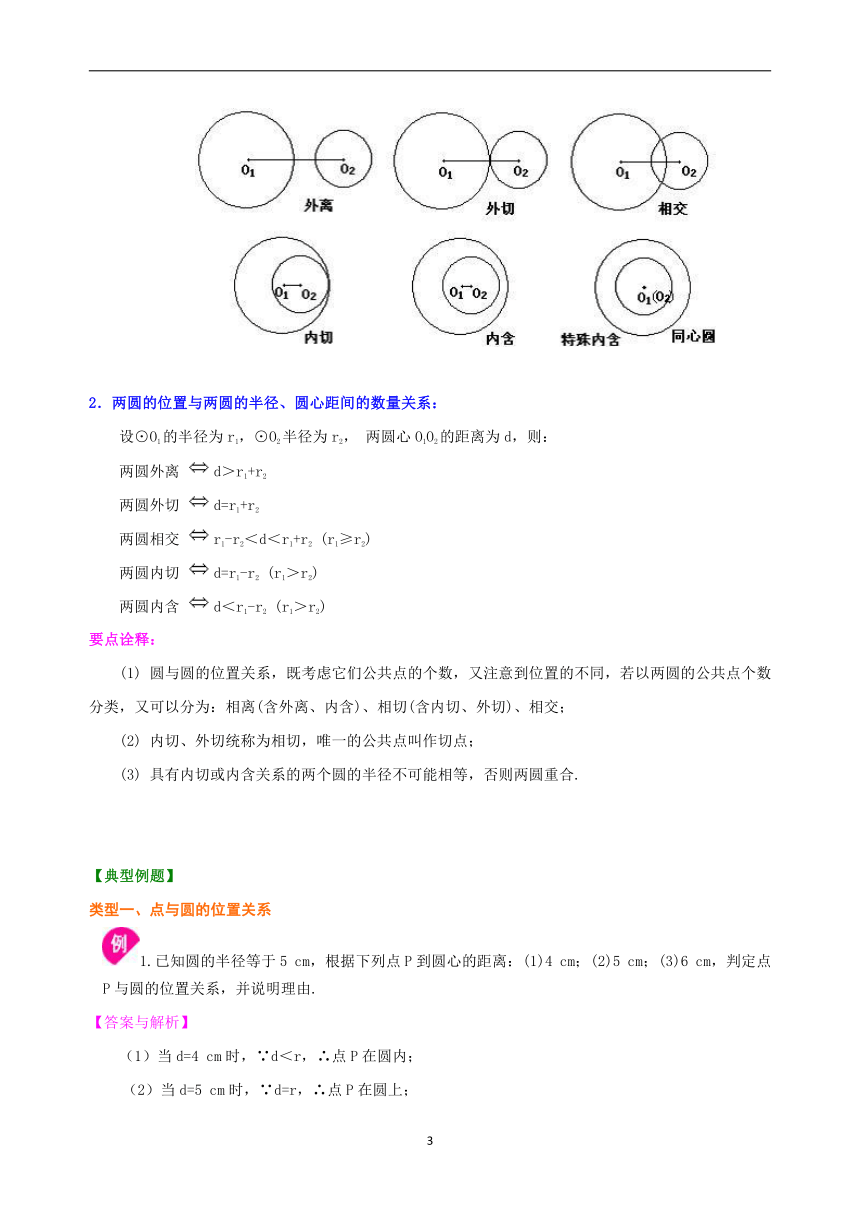
要点三、圆和圆的位置关系 1.圆与圆的五种位置关系的定义 两圆外离:两个圆没有公共点,且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离. 两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一的公共点叫做切点. 两圆相交:两个圆有两个公共点时,叫做这两圆相交. 两圆内切:两个圆有唯一公共点,并且除了这个公共点外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点. 两圆内含:两个圆没有公共点,且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含. / 2.两圆的位置与两圆的半径、圆心距间的数量关系: 设⊙O1的半径为r1,⊙O2半径为r2, 两圆心O1O2的距离为d,则: 两圆外离 /d>r1+r2 两圆外切 /d=r1+r2 两圆相交 /r1-r2<d<r1+r2 (r1≥r2) 两圆内切 /d=r1-r2 (r1>r2) 两圆内含 /d<r1-r2 (r1>r2) 要点诠释: (1) 圆与圆的位置关系,既考虑它们公共点的个数,又注意到位置的不同,若以两圆的公共点个数 分类,又可以分为:相离(含外离、内含)、相切(含内切、外切)、相交; (2) 内切、外切统称为相切,唯一的公共点叫作切点; (3) 具有内切或内含关系的两个圆的半径不可能相等,否则两圆重合.
【典型例题】
类型一、点与圆的位置关系
/1.已知圆的半径等于5 cm,根据下列点P到圆心的距离:(1)4 cm;(2)5 cm;(3)6 cm,判定点P与圆的位置关系,并说明理由.
【答案与解析】
(1)当d=4 cm时,∵d<r,∴点P在圆内;
(2)当d=5 cm时,∵d=r,∴点P在圆上;
(3)当d=6 cm时,∵d>r,∴点P在圆外.
【总结升华】利用点与圆的位置关系,由点到圆心的距离与半径的大小比较.
举一反三:
【变式】点A在以O为圆心,3 为半径的⊙O内,则点A到圆心O的距离d的范围是________.
【答案】0≤d<3.
类型二、直线与圆的位置关系
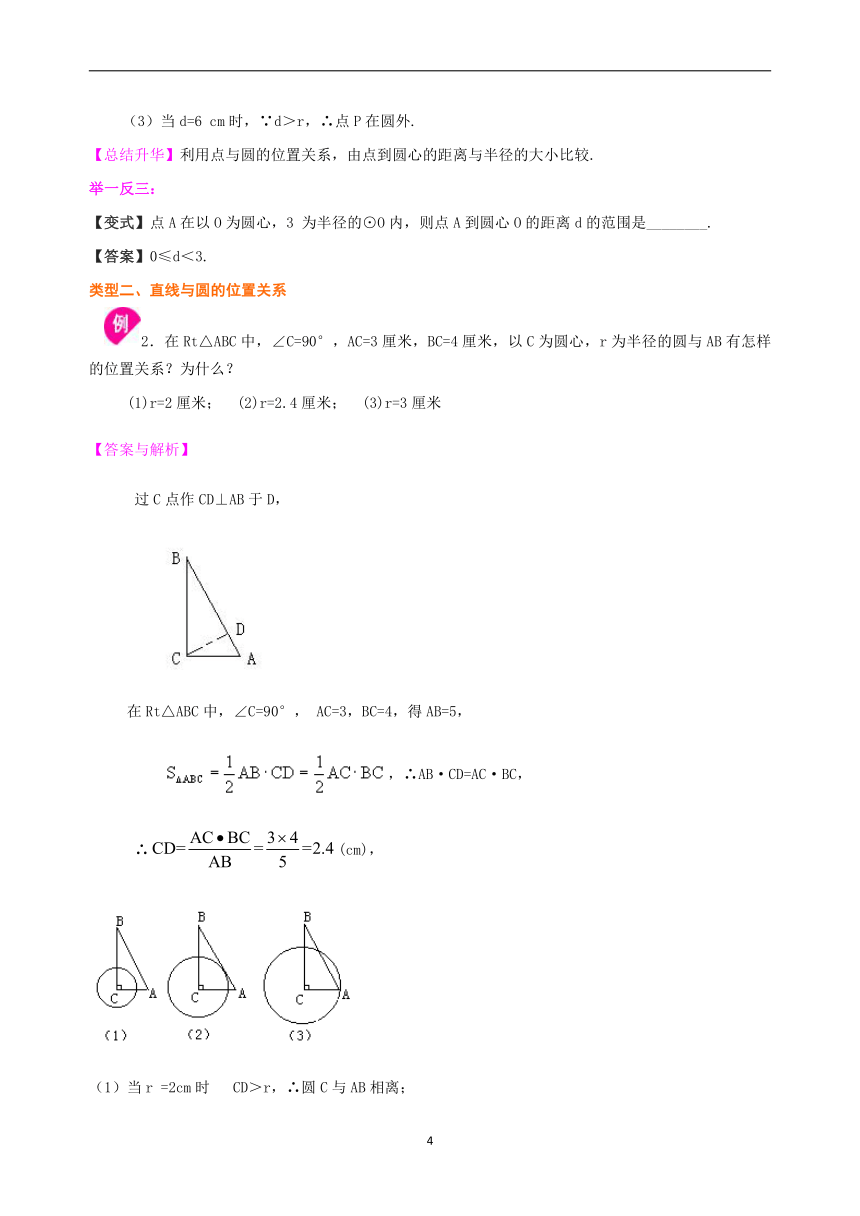
/2.在Rt△ABC中,∠C=90°,AC=3厘米,BC=4厘米,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2厘米; (2)r=2.4厘米; (3)r=3厘米
【答案与解析】
过C点作CD⊥AB于D,
/
在Rt△ABC中,∠C=90°, AC=3,BC=4,得AB=5,
??? /,∴AB·CD=AC·BC,
∴/(cm),
/
(1)当r =2cm时? CD>r,∴圆C与AB相离;
(2)当r= 2.4cm时,CD=r,∴圆C与AB相切;
(3)当r=3cm时,CD<r,∴圆C与AB相交.
【总结升华】欲判定⊙C与直线AB的关系,只需先求出圆心C到直线AB的距离CD的长,然后再与r比较即可.
举一反三:
【变式】(2019?齐齐哈尔)如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
/
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
【答案】A;
提示:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2/=8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故选:A.
/3.如图所示,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证:直线AC与⊙D相切.
/
【答案与解析】
过D作DF⊥AC于F.
∵ ∠B=90°,∴ DB⊥AB.
又AD平分∠BAC,
∴ DF=BD=半径.
∴ AC与⊙D相切.
/
【总结升华】如果已知条件中不知道直线与圆有公共点,其证法是过圆心作直线的垂线段,再证明垂线段的长等于半径的长即可.
类型三、三角形的外接圆
/4.如图,已知△ABC,请作出该三角形的外接圆⊙O(要求尺规作图,保留作图痕迹,不要写作图过程).
/
【思路点拨】由于三角形的外心是三角形三边中垂线的交点,可作出△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心(设为O);再以O为圆心,OB长为半径作圆,即可得出△ABC的外接圆.
【答案与解析】
解:如图所示:⊙O即为△ABC的外接圆.
/
【总结升华】此题主要考查的是三角形外接圆的作法,关键是作出任意两边的垂直平分线,找出外接圆的圆心.
举一反三:
【变式】直角三角形的两条直角边分别为5和12,则其外接圆半径的长为
【答案】6.5.
类型四、圆与圆的位置关系
/5.(1)已知两圆的半径分别为3cm,5cm,且其圆心距为7cm,则这两圆的位置关系是( )
A.外切 B.内切 C.相交 D.相离
(2)已知⊙O1与⊙O2相切,⊙O1的半径为3cm,⊙O2的半径为2cm,则O1O2的长是( )
A.1cm B.5cm C.1cm或5cm D.0.5cm或2.5cm
【答案】(1)C ; (2)C.
【解析】(1)由于圆心距d=7cm,R+r=5+3=8(cm),R-r=5-3=2(cm).
∴ R-r<d<R+r,故这两圆的位置关系是相交.
(2)两圆相切包括外切和内切,当⊙O1与⊙O2外切时,d=O1O2=R+r=3+2=5(cm);
当⊙O1与⊙O2内切时,d=O1O2=R-r=3-2=1(cm).
【总结升华】由数量确定位置或由位置确定数量的依据是:①两圆外离/d>R+r;②两圆外切/d=R+r;③两圆相交/R-r<d<R+r;④两圆内切/d=R-r;⑤两圆内含/d<R-r.
点、直线、圆与圆的位置关系—巩固练习(基础)
【巩固练习】
一、选择题
1.(2019?张家界)如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
/
A.相离 B.相交 C.相切 D.以上三种情况均有可能
2.(2019?岳池县模拟)在△ABC中,∠A=90°,AB=3cm,AC=4cm,若以A为圆心3cm为半径作⊙O,则BC与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.不能确定
3.设⊙O的半径为3,点O到直线l的距离为d,若直线l与⊙O至少有一个公共点,则d应满足的条件是( )
A.d=3 B. d<3 C. d≤3 D.d>3
4.在Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为( ) .
A.8 B.4 C.9.6 D.4.8
5.已知⊙O1和⊙O2的半径分别为1和5,圆心距为3,则两圆的位置关系是( )
A.相交 B. 内切 C. 外切 D.内含
6.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( ).
A.点D在⊙A外 B.点D在⊙A 上 C. 点D在⊙A内 D.不能确定
二、填空题
7.(2019?巴中模拟)已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,/,那么点P与⊙O的位置关系是 .
8.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.
9.锐角三角形的外心在三角形的___________部,钝角三角形的外心在三角形的_____________部,
直角三角形的外心在________________.
10.(2019?金山区一模)已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值范围是 .
11.(2019?盐城)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
/
12.如图,施工工地的水平地面上,有三根外径都是1 m的水泥管,两两相切地堆放在一起,其最高点到地面的距离是_________.
/
三、解答题
13. 在Rt△ABO中,∠AOB=90°,OA= ,OB=,以O为圆心,4为半径的⊙O与直线AB的位置关系如何?请说明理由.
/
14.(2019秋?静宁县期末)在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
(1)r=4cm;
(2)r=4.8cm;
(3)r=6cm.
/
15.(2019秋?石河子校级月考)如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
(2)若以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
/
【答案与解析】
一、选择题 1.【答案】C;
【解析】过点C作CD⊥AO于点D,
∵∠O=30°,OC=6,
∴DC=3,
∴以点C为圆心,半径为3的圆与OA的位置关系是:相切.
故选:C.
2.【答案】A;
【解析】做AD⊥BC,
∵∠A=90°,AB=3cm,AC=4cm,若以A为圆心3cm为半径作⊙O,
∴BC=5,
∴AD×BC=AC×AB,
解得:AD=2.4,2.4<3,
∴BC与⊙O的位置关系是:相交.
故选A.
3.【答案】C;
【解析】直线l可能和圆相交或相切.
4.【答案】D;
【解析】作CD⊥AB于D,则CD为⊙C的半径,BC=/=/=8,
由面积相等,得AB·CD=AC·BC.
∴CD=/=4.8.
5.【答案】D;
【解析】内切、外切分别对应d=R+r,d=R-r,它们起着分界作用.在⊙O1和⊙O2相对运动时依次产生外离、外切、相交、内切、内含五种位置关系,圆心距逐渐变小,而相内切和外切起着分界作用,所以先计算d+r和d-r,因为圆心距d=3<R-r,所以“内含”.
6. 【答案】A;
【解析】由勾股定理得,斜边AB的长为,斜边的一半为 ,而,所以点在圆外.
二、填空题
7.【答案】无法确定.
【解析】∵PA=/,⊙O的直径为2
∴点P的位置有三种情况:①在圆外,②在圆上,③在圆内.所以无法确定点P与⊙O的位置关系.
8.【答案】26cm.
9.【答案】内,外,它的斜边中点处.
10.【答案】OA>5.
11.【答案】3<r<5.
【解析】在直角△ABD中,CD=AB=4,AD=3,
则BD=/=5.
由图可知3<r<5.
12.【答案】.
【解析】由于三个圆两两外切,所以圆心距等于半径之和,所以三个圆心为顶点的三角形是边长
为1 m的等边三角形,最高点到地面距离是等边三角形的高加上一个直径.
等边三角形的高是/,故最高点到地面的距离是.
三、解答题
13.【答案与解析】
解:如图,作OC⊥AB于点C,
∴Rt△ABO中,∠AOB=90°,OA=,OB=,
∴AB=
∵AB×OC=OA×OB,
∴OC=
∵⊙O的半径为4,
∴相切.
14.【答案与解析】
解:过点C作CD⊥AB于点D.
则CD=/=4.8(cm).
(1)∵当r=4cm时,CD>r,∴⊙C与直线AB相离.
(2)∵当r=4.8cm时,CD=r,∴⊙C与直线AB相切.
(3)∵当r=6cm时,CD<r,∴⊙C与直线AB相交.
15.【答案与解析】
解:(1)连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3<r<5.
/
【学习目标】
1. 理解点与圆的位置关系由点到圆心的距离决定;会画三角形的外接圆,熟识相关概念.
2. 理解直线与圆的各种位置关系, 会用点到直线的距离来判断直线与圆的位置关系; 3.了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交,圆心距等概念.理解两圆的位
置关系与d、r1、r2等量关系的等价条件并灵活应用它们解题.
【要点梳理】
要点一、点和圆的位置关系 1.点和圆的三种位置关系:
由于平面上圆的存在,就把平面上的点分成了三个集合,即圆内的点,圆上的点和圆外的点,这三类点各具有相同的性质和判定方法;设⊙O的半径为r,点P到圆心的距离为d,则有 / / / /
2.三角形的外接圆
经过三角形的三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心. 三角形的外心到三角形三个顶点的距离相等.
要点诠释:
(1)点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系;
(2)不在同一直线上的三个点确定一个圆. 要点二、直线和圆的位置关系
1.直线和圆的三种位置关系: (1) 相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线. (2) 相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点. (3) 相离:直线和圆没有公共点时,叫做直线和圆相离. 2.直线与圆的位置关系的判定和性质. 直线与圆的位置关系能否像点与圆的位置关系一样通过一些条件来进行分析判断呢? 由于圆心确定圆的位置,半径确定圆的大小,因此研究直线和圆的位置关系,就可以转化为直线和点(圆心)的位置关系.下面图(1)中直线与圆心的距离小于半径;图(2)中直线与圆心的距离等于半径;图(3)中直线与圆心的距离大于半径. / 如果⊙O的半径为r,圆心O到直线/的距离为d,那么 /
要点诠释: 这三个命题从左边到右边反映了直线与圆的位置关系所具有的性质;从右边到左边则是直线与圆的位置关系的判定.
要点三、圆和圆的位置关系 1.圆与圆的五种位置关系的定义 两圆外离:两个圆没有公共点,且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离. 两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一的公共点叫做切点. 两圆相交:两个圆有两个公共点时,叫做这两圆相交. 两圆内切:两个圆有唯一公共点,并且除了这个公共点外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点. 两圆内含:两个圆没有公共点,且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含. / 2.两圆的位置与两圆的半径、圆心距间的数量关系: 设⊙O1的半径为r1,⊙O2半径为r2, 两圆心O1O2的距离为d,则: 两圆外离 /d>r1+r2 两圆外切 /d=r1+r2 两圆相交 /r1-r2<d<r1+r2 (r1≥r2) 两圆内切 /d=r1-r2 (r1>r2) 两圆内含 /d<r1-r2 (r1>r2) 要点诠释: (1) 圆与圆的位置关系,既考虑它们公共点的个数,又注意到位置的不同,若以两圆的公共点个数 分类,又可以分为:相离(含外离、内含)、相切(含内切、外切)、相交; (2) 内切、外切统称为相切,唯一的公共点叫作切点; (3) 具有内切或内含关系的两个圆的半径不可能相等,否则两圆重合.
【典型例题】
类型一、点与圆的位置关系
/1.已知圆的半径等于5 cm,根据下列点P到圆心的距离:(1)4 cm;(2)5 cm;(3)6 cm,判定点P与圆的位置关系,并说明理由.
【答案与解析】
(1)当d=4 cm时,∵d<r,∴点P在圆内;
(2)当d=5 cm时,∵d=r,∴点P在圆上;
(3)当d=6 cm时,∵d>r,∴点P在圆外.
【总结升华】利用点与圆的位置关系,由点到圆心的距离与半径的大小比较.
举一反三:
【变式】点A在以O为圆心,3 为半径的⊙O内,则点A到圆心O的距离d的范围是________.
【答案】0≤d<3.
类型二、直线与圆的位置关系
/2.在Rt△ABC中,∠C=90°,AC=3厘米,BC=4厘米,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2厘米; (2)r=2.4厘米; (3)r=3厘米
【答案与解析】
过C点作CD⊥AB于D,
/
在Rt△ABC中,∠C=90°, AC=3,BC=4,得AB=5,
??? /,∴AB·CD=AC·BC,
∴/(cm),
/
(1)当r =2cm时? CD>r,∴圆C与AB相离;
(2)当r= 2.4cm时,CD=r,∴圆C与AB相切;
(3)当r=3cm时,CD<r,∴圆C与AB相交.
【总结升华】欲判定⊙C与直线AB的关系,只需先求出圆心C到直线AB的距离CD的长,然后再与r比较即可.
举一反三:
【变式】(2019?齐齐哈尔)如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
/
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
【答案】A;
提示:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2/=8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故选:A.
/3.如图所示,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证:直线AC与⊙D相切.
/
【答案与解析】
过D作DF⊥AC于F.
∵ ∠B=90°,∴ DB⊥AB.
又AD平分∠BAC,
∴ DF=BD=半径.
∴ AC与⊙D相切.
/
【总结升华】如果已知条件中不知道直线与圆有公共点,其证法是过圆心作直线的垂线段,再证明垂线段的长等于半径的长即可.
类型三、三角形的外接圆
/4.如图,已知△ABC,请作出该三角形的外接圆⊙O(要求尺规作图,保留作图痕迹,不要写作图过程).
/
【思路点拨】由于三角形的外心是三角形三边中垂线的交点,可作出△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心(设为O);再以O为圆心,OB长为半径作圆,即可得出△ABC的外接圆.
【答案与解析】
解:如图所示:⊙O即为△ABC的外接圆.
/
【总结升华】此题主要考查的是三角形外接圆的作法,关键是作出任意两边的垂直平分线,找出外接圆的圆心.
举一反三:
【变式】直角三角形的两条直角边分别为5和12,则其外接圆半径的长为
【答案】6.5.
类型四、圆与圆的位置关系
/5.(1)已知两圆的半径分别为3cm,5cm,且其圆心距为7cm,则这两圆的位置关系是( )
A.外切 B.内切 C.相交 D.相离
(2)已知⊙O1与⊙O2相切,⊙O1的半径为3cm,⊙O2的半径为2cm,则O1O2的长是( )
A.1cm B.5cm C.1cm或5cm D.0.5cm或2.5cm
【答案】(1)C ; (2)C.
【解析】(1)由于圆心距d=7cm,R+r=5+3=8(cm),R-r=5-3=2(cm).
∴ R-r<d<R+r,故这两圆的位置关系是相交.
(2)两圆相切包括外切和内切,当⊙O1与⊙O2外切时,d=O1O2=R+r=3+2=5(cm);
当⊙O1与⊙O2内切时,d=O1O2=R-r=3-2=1(cm).
【总结升华】由数量确定位置或由位置确定数量的依据是:①两圆外离/d>R+r;②两圆外切/d=R+r;③两圆相交/R-r<d<R+r;④两圆内切/d=R-r;⑤两圆内含/d<R-r.
点、直线、圆与圆的位置关系—巩固练习(基础)
【巩固练习】
一、选择题
1.(2019?张家界)如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
/
A.相离 B.相交 C.相切 D.以上三种情况均有可能
2.(2019?岳池县模拟)在△ABC中,∠A=90°,AB=3cm,AC=4cm,若以A为圆心3cm为半径作⊙O,则BC与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.不能确定
3.设⊙O的半径为3,点O到直线l的距离为d,若直线l与⊙O至少有一个公共点,则d应满足的条件是( )
A.d=3 B. d<3 C. d≤3 D.d>3
4.在Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为( ) .
A.8 B.4 C.9.6 D.4.8
5.已知⊙O1和⊙O2的半径分别为1和5,圆心距为3,则两圆的位置关系是( )
A.相交 B. 内切 C. 外切 D.内含
6.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( ).
A.点D在⊙A外 B.点D在⊙A 上 C. 点D在⊙A内 D.不能确定
二、填空题
7.(2019?巴中模拟)已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,/,那么点P与⊙O的位置关系是 .
8.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.
9.锐角三角形的外心在三角形的___________部,钝角三角形的外心在三角形的_____________部,
直角三角形的外心在________________.
10.(2019?金山区一模)已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值范围是 .
11.(2019?盐城)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
/
12.如图,施工工地的水平地面上,有三根外径都是1 m的水泥管,两两相切地堆放在一起,其最高点到地面的距离是_________.
/
三、解答题
13. 在Rt△ABO中,∠AOB=90°,OA= ,OB=,以O为圆心,4为半径的⊙O与直线AB的位置关系如何?请说明理由.
/
14.(2019秋?静宁县期末)在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
(1)r=4cm;
(2)r=4.8cm;
(3)r=6cm.
/
15.(2019秋?石河子校级月考)如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
(2)若以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
/
【答案与解析】
一、选择题 1.【答案】C;
【解析】过点C作CD⊥AO于点D,
∵∠O=30°,OC=6,
∴DC=3,
∴以点C为圆心,半径为3的圆与OA的位置关系是:相切.
故选:C.
2.【答案】A;
【解析】做AD⊥BC,
∵∠A=90°,AB=3cm,AC=4cm,若以A为圆心3cm为半径作⊙O,
∴BC=5,
∴AD×BC=AC×AB,
解得:AD=2.4,2.4<3,
∴BC与⊙O的位置关系是:相交.
故选A.
3.【答案】C;
【解析】直线l可能和圆相交或相切.
4.【答案】D;
【解析】作CD⊥AB于D,则CD为⊙C的半径,BC=/=/=8,
由面积相等,得AB·CD=AC·BC.
∴CD=/=4.8.
5.【答案】D;
【解析】内切、外切分别对应d=R+r,d=R-r,它们起着分界作用.在⊙O1和⊙O2相对运动时依次产生外离、外切、相交、内切、内含五种位置关系,圆心距逐渐变小,而相内切和外切起着分界作用,所以先计算d+r和d-r,因为圆心距d=3<R-r,所以“内含”.
6. 【答案】A;
【解析】由勾股定理得,斜边AB的长为,斜边的一半为 ,而,所以点在圆外.
二、填空题
7.【答案】无法确定.
【解析】∵PA=/,⊙O的直径为2
∴点P的位置有三种情况:①在圆外,②在圆上,③在圆内.所以无法确定点P与⊙O的位置关系.
8.【答案】26cm.
9.【答案】内,外,它的斜边中点处.
10.【答案】OA>5.
11.【答案】3<r<5.
【解析】在直角△ABD中,CD=AB=4,AD=3,
则BD=/=5.
由图可知3<r<5.
12.【答案】.
【解析】由于三个圆两两外切,所以圆心距等于半径之和,所以三个圆心为顶点的三角形是边长
为1 m的等边三角形,最高点到地面距离是等边三角形的高加上一个直径.
等边三角形的高是/,故最高点到地面的距离是.
三、解答题
13.【答案与解析】
解:如图,作OC⊥AB于点C,
∴Rt△ABO中,∠AOB=90°,OA=,OB=,
∴AB=
∵AB×OC=OA×OB,
∴OC=
∵⊙O的半径为4,
∴相切.
14.【答案与解析】
解:过点C作CD⊥AB于点D.
则CD=/=4.8(cm).
(1)∵当r=4cm时,CD>r,∴⊙C与直线AB相离.
(2)∵当r=4.8cm时,CD=r,∴⊙C与直线AB相切.
(3)∵当r=6cm时,CD<r,∴⊙C与直线AB相交.
15.【答案与解析】
解:(1)连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3<r<5.
/
同课章节目录
