人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):41【基础】正多边形和圆(附答案)
文档属性
| 名称 | 人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):41【基础】正多边形和圆(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 382.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 23:00:40 | ||
图片预览


文档简介
正多边形和圆—知识讲解(基础)
【学习目标】
1.了解正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正
多边形;
3.会进行正多边形的有关计算.
【要点梳理】
知识点一、正多边形的概念 各边相等,各角也相等的多边形是正多边形. 要点诠释: 判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
知识点二、正多边形的重要元素 1.正多边形的外接圆和圆的内接正多边形 正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆. 2.正多边形的有关概念 (1)一个正多边形的外接圆的圆心叫做这个正多边形的中心. (2)正多边形外接圆的半径叫做正多边形的半径. (3)正多边形每一边所对的圆心角叫做正多边形的中心角. (4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距. 3.正多边形的有关计算 (1)正n边形每一个内角的度数是; (2)正n边形每个中心角的度数是; (3)正n边形每个外角的度数是.
要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
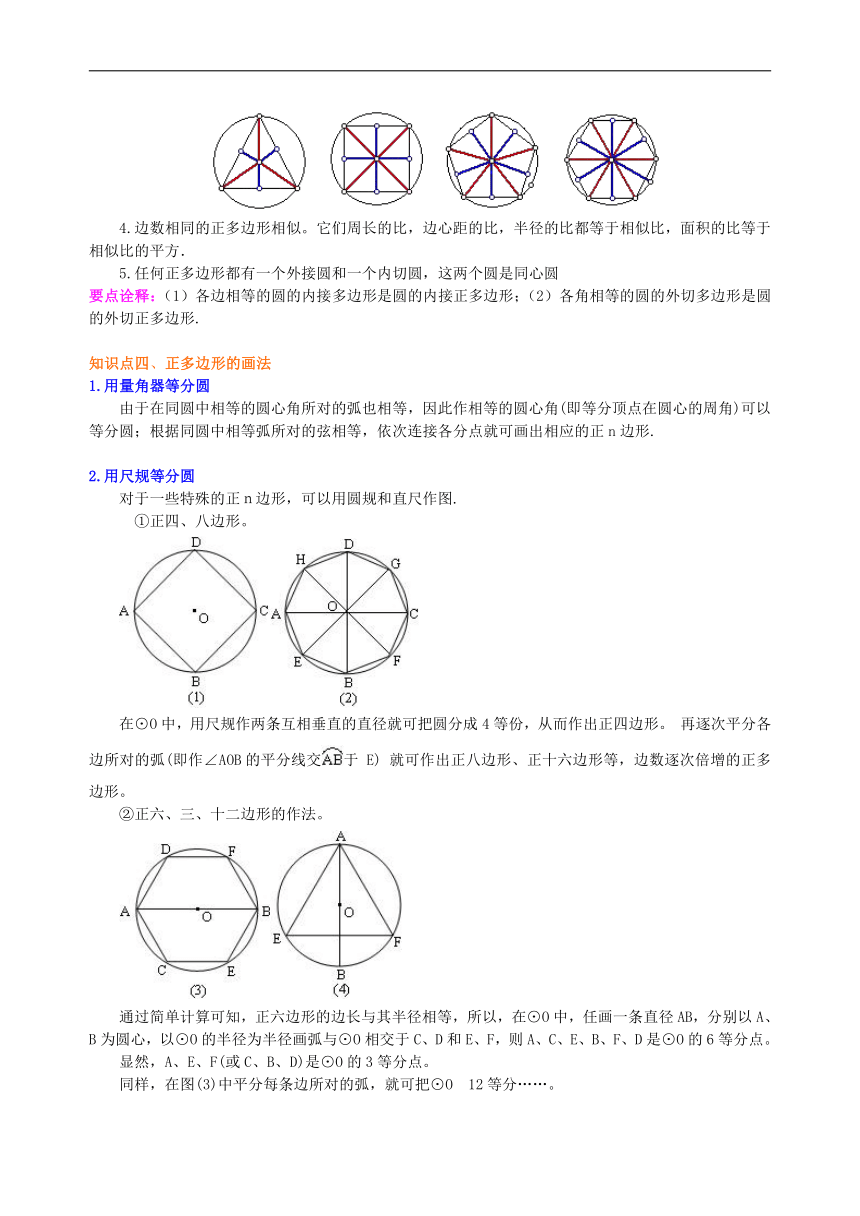
知识点三、正多边形的性质 1.正多边形都只有一个外接圆,圆有无数个内接正多边形. 2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形. 3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心. 4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆 要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.
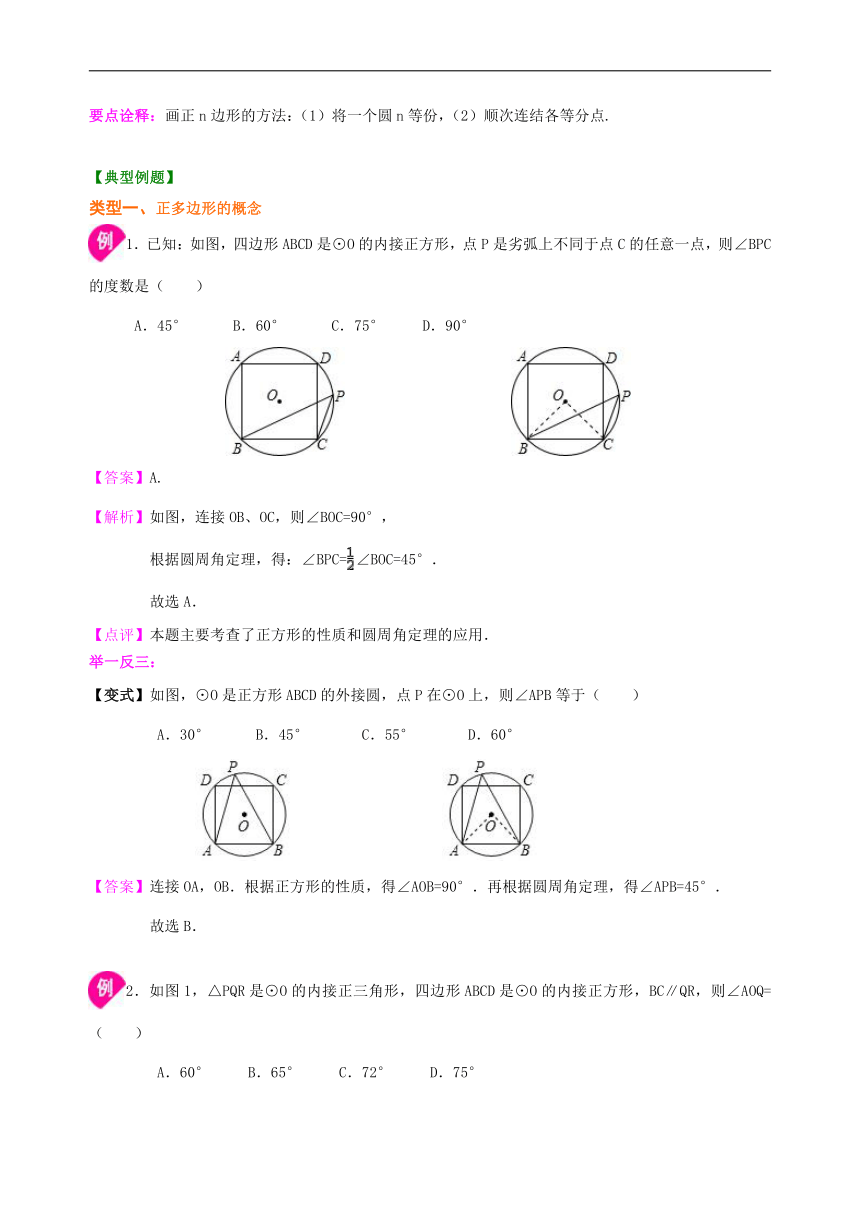
知识点四、正多边形的画法 1.用量角器等分圆 由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形. 2.用尺规等分圆 对于一些特殊的正n边形,可以用圆规和直尺作图. ①正四、八边形。 在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形。 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形。 ②正六、三、十二边形的作法。 通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点。 显然,A、E、F(或C、B、D)是⊙O的3等分点。 同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分……。 要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.
【典型例题】
类型一、正多边形的概念
1.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
【答案】A.
【解析】如图,连接OB、OC,则∠BOC=90°, 根据圆周角定理,得:∠BPC=∠BOC=45°. 故选A.
【点评】本题主要考查了正方形的性质和圆周角定理的应用. 举一反三:
【变式】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )
A.30° B.45° C.55° D.60°
【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°. 故选B.
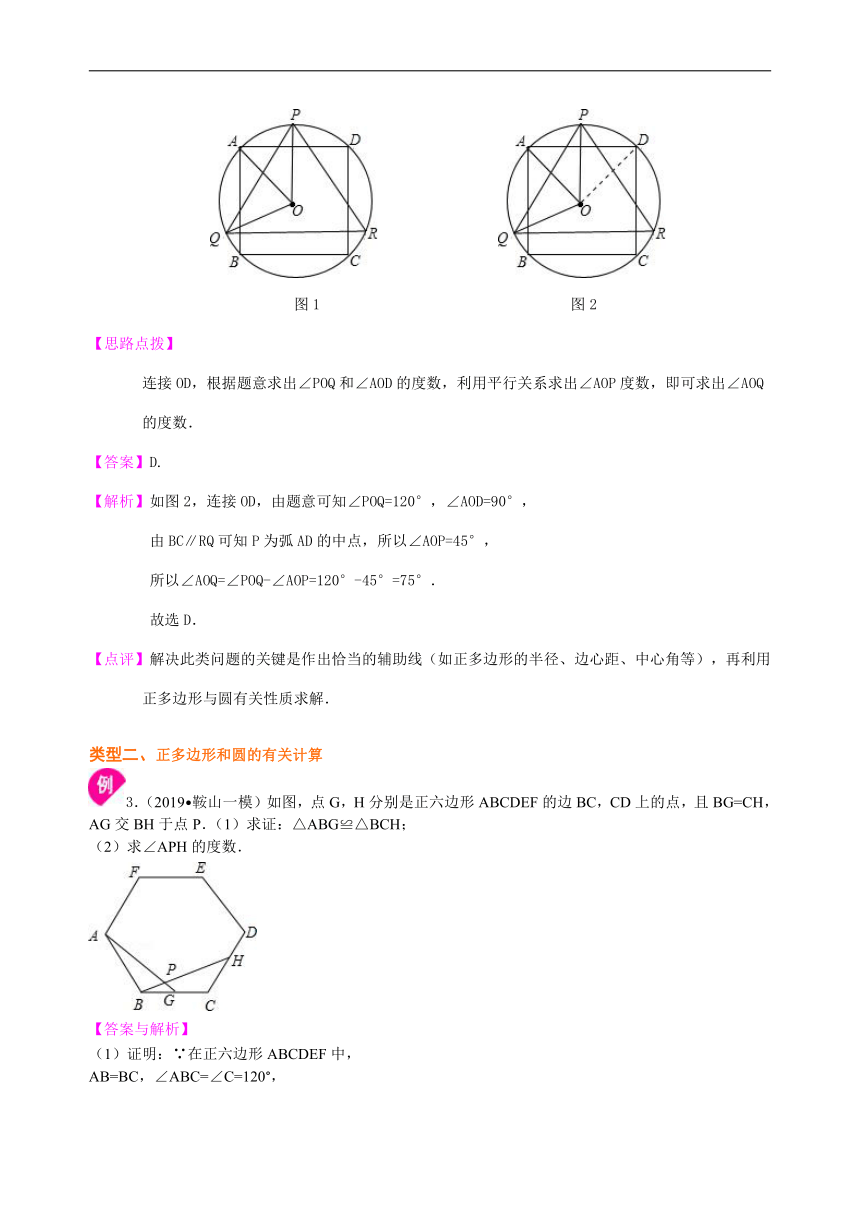
2.如图1,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
图1 图2
【思路点拨】
连接OD,根据题意求出∠POQ和∠AOD的度数,利用平行关系求出∠AOP度数,即可求出∠AOQ的度数.
【答案】D.
【解析】如图2,连接OD,由题意可知∠POQ=120°,∠AOD=90°, 由BC∥RQ可知P为弧AD的中点,所以∠AOP=45°, 所以∠AOQ=∠POQ-∠AOP=120°-45°=75°. 故选D.
【点评】解决此类问题的关键是作出恰当的辅助线(如正多边形的半径、边心距、中心角等),再利用正多边形与圆有关性质求解.
类型二、正多边形和圆的有关计算
3.(2019?鞍山一模)如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
【答案与解析】
(1)证明:∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中,
∴△ABG≌△BCH;
(2)解:由(1)知:△ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
【点评】本题考查了正多边形的性质及相关计算,解题的关键是正确地利用正六边形中相等的元素.
4.(2019?道里区二模)若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3,a4,a6,则a3:a4:a6等于( )
A.1:: B. 1:2:3 C. 3:2:1 D. ::1
【思路点拨】从中心向边作垂线,构建直角三角来解决.
【答案】D.
【解析】解:设圆的半径是r,
则多边形的半径是r,
如图1,则内接正三角形的边长a3=r,
如图2,内接正方形的边长是a4=r,
如图3,正六边形的边长是a6=r,
因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比a3:a4:a6=::1.
故选D.
【点评】本题考查了正多边形和圆,正多边形的计算一般是通过中心作边的垂线,连接半径,构造直角三角形来求解.
举一反三:
【变式】如图是对称中心为点的正六边形.如果用一个含角的直角三角板的角,借助点(使角的顶点落在点处),把这个正六边形的面积等分,那么的所有可能的值是?___________ __?.
【答案】
根据圆内接正多边形的性质可知,只要把此正六边形再化为正多边形即可, 即可知:360÷30=12; 360÷60=6; 360÷90=4; 360÷120=3; 360÷180=2. 故么n的所有可能的值是2,3,4,6,12.
正多边形和圆—巩固练习(基础)
【巩固练习】
一、选择题 1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )
A.9 B.8 C.7 D.6
2.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A. cm B. cm C.cm D.1 cm
第2题图 第5题图
3.(2019?广州)已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B. 9 C. 18 D. 36
4.正三角形、正方形、圆三者的周长都等于,它们的面积分别为S1,S2、S3,则( ).
A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S3
5.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).
A.30° B.35° C.36° D.37°
第6题图 第7题图 第9题图
6.如图所示,是由5把相同的折扇组成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
二、填空题
7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠等于________.
8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________.
9.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径是________.
10.(2019?铁岭)如图,点O是正五边形ABCDE的中心,则∠BAO的度数为 .
11.正六边形的半径是5cm,则边长________,周长________ ,边心距________,面积________.
12. 正六边形的外接圆的半径与内切圆的半径之比为 .
三、解答题
13.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S.
14. 如图所示,半径为R的圆绕周长为10πR的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈?
一位同学的解答过程:圆的周长为2πR,所以它绕完正六边形后一共转了圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.
15.(2019秋?吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
【答案与解析】
一、选择题
1.【答案】D;
【解析】可求每个外角为60°,∴ 360÷60=6或 ∴ n=6.
2.【答案】A;
【解析】较长对角线与较短对角线及一边长构成一直角三角形,用勾股定理求解.
3.【答案】C;
【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2,高为3,
因而等边三角形的面积是3,
∴正六边形的面积=18,
故选C.
4.【答案】C;
【解析】当周长一定时,边数越多的正多边形其面积越大,当它成为圆时面积最大.
5.【答案】C;
【解析】五角星的每一个角所对的弧为圆的,∴ 弧的度数为72°,因而每个角的度数为36°,
故选C.
6.【答案】D.
【解析】如图③所示,正五边形ABCDE的中心角为72°,各内角为108°,故五角星五个锐角均为48°.
二、填空题
7.【答案】72°;
【解析】=360°-90°-90°-108°=72°.
8.【答案】;
【解析】如图所示,△ABC为等腰Rt△,.
9.【答案】cm;
【解析】过O作OD⊥BC于D,连接OB,在Rt△BOD中,BD=BC==5(cm).
∠BOD=,
∴ .
∴ BO=(cm).
10.【答案】54°;
【解析】连接OB,
则OB=OA,
∴∠BAO=∠ABO,
∵点O是正五边形ABCDE的中心,
∴∠AOB==72°,
∴∠BAO=(180°﹣72°)=54°;
故答案为:54°.
11.【答案】5cm,30cm,cm,;
12.【答案】2:.
【解析】设正六边形的半径是r,则外接圆的半径r, 内切圆的半径是正六边形的边心距,因而是, 因而正六边形的外接圆的半径与内切圆的半径之比为2:.
三、解答题
13.【答案与解析】
作AD⊥BC于D.
∵ △ABC是正三角形,
∴ 点O在AD上,a=BC=2CD,∠OCD=30°,
在Rt△COD中,,
,
∴ ,.
又∵ AD=OA+OD=2+1=3,
∴ ,
∴ ,,,.
14.【答案与解析】
有错误,由正六边形的每个顶点外圆要转60°角,应转了(圈).
15.【答案与解析】
解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=5×=5(cm).
即⊙O的半径R=5cm.
【学习目标】
1.了解正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正
多边形;
3.会进行正多边形的有关计算.
【要点梳理】
知识点一、正多边形的概念 各边相等,各角也相等的多边形是正多边形. 要点诠释: 判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
知识点二、正多边形的重要元素 1.正多边形的外接圆和圆的内接正多边形 正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆. 2.正多边形的有关概念 (1)一个正多边形的外接圆的圆心叫做这个正多边形的中心. (2)正多边形外接圆的半径叫做正多边形的半径. (3)正多边形每一边所对的圆心角叫做正多边形的中心角. (4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距. 3.正多边形的有关计算 (1)正n边形每一个内角的度数是; (2)正n边形每个中心角的度数是; (3)正n边形每个外角的度数是.
要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
知识点三、正多边形的性质 1.正多边形都只有一个外接圆,圆有无数个内接正多边形. 2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形. 3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心. 4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆 要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.
知识点四、正多边形的画法 1.用量角器等分圆 由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形. 2.用尺规等分圆 对于一些特殊的正n边形,可以用圆规和直尺作图. ①正四、八边形。 在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形。 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形。 ②正六、三、十二边形的作法。 通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点。 显然,A、E、F(或C、B、D)是⊙O的3等分点。 同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分……。 要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.
【典型例题】
类型一、正多边形的概念
1.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
【答案】A.
【解析】如图,连接OB、OC,则∠BOC=90°, 根据圆周角定理,得:∠BPC=∠BOC=45°. 故选A.
【点评】本题主要考查了正方形的性质和圆周角定理的应用. 举一反三:
【变式】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )
A.30° B.45° C.55° D.60°
【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°. 故选B.
2.如图1,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
图1 图2
【思路点拨】
连接OD,根据题意求出∠POQ和∠AOD的度数,利用平行关系求出∠AOP度数,即可求出∠AOQ的度数.
【答案】D.
【解析】如图2,连接OD,由题意可知∠POQ=120°,∠AOD=90°, 由BC∥RQ可知P为弧AD的中点,所以∠AOP=45°, 所以∠AOQ=∠POQ-∠AOP=120°-45°=75°. 故选D.
【点评】解决此类问题的关键是作出恰当的辅助线(如正多边形的半径、边心距、中心角等),再利用正多边形与圆有关性质求解.
类型二、正多边形和圆的有关计算
3.(2019?鞍山一模)如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
【答案与解析】
(1)证明:∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中,
∴△ABG≌△BCH;
(2)解:由(1)知:△ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
【点评】本题考查了正多边形的性质及相关计算,解题的关键是正确地利用正六边形中相等的元素.
4.(2019?道里区二模)若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3,a4,a6,则a3:a4:a6等于( )
A.1:: B. 1:2:3 C. 3:2:1 D. ::1
【思路点拨】从中心向边作垂线,构建直角三角来解决.
【答案】D.
【解析】解:设圆的半径是r,
则多边形的半径是r,
如图1,则内接正三角形的边长a3=r,
如图2,内接正方形的边长是a4=r,
如图3,正六边形的边长是a6=r,
因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比a3:a4:a6=::1.
故选D.
【点评】本题考查了正多边形和圆,正多边形的计算一般是通过中心作边的垂线,连接半径,构造直角三角形来求解.
举一反三:
【变式】如图是对称中心为点的正六边形.如果用一个含角的直角三角板的角,借助点(使角的顶点落在点处),把这个正六边形的面积等分,那么的所有可能的值是?___________ __?.
【答案】
根据圆内接正多边形的性质可知,只要把此正六边形再化为正多边形即可, 即可知:360÷30=12; 360÷60=6; 360÷90=4; 360÷120=3; 360÷180=2. 故么n的所有可能的值是2,3,4,6,12.
正多边形和圆—巩固练习(基础)
【巩固练习】
一、选择题 1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )
A.9 B.8 C.7 D.6
2.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A. cm B. cm C.cm D.1 cm
第2题图 第5题图
3.(2019?广州)已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B. 9 C. 18 D. 36
4.正三角形、正方形、圆三者的周长都等于,它们的面积分别为S1,S2、S3,则( ).
A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S3
5.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).
A.30° B.35° C.36° D.37°
第6题图 第7题图 第9题图
6.如图所示,是由5把相同的折扇组成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
二、填空题
7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠等于________.
8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________.
9.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径是________.
10.(2019?铁岭)如图,点O是正五边形ABCDE的中心,则∠BAO的度数为 .
11.正六边形的半径是5cm,则边长________,周长________ ,边心距________,面积________.
12. 正六边形的外接圆的半径与内切圆的半径之比为 .
三、解答题
13.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S.
14. 如图所示,半径为R的圆绕周长为10πR的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈?
一位同学的解答过程:圆的周长为2πR,所以它绕完正六边形后一共转了圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.
15.(2019秋?吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
【答案与解析】
一、选择题
1.【答案】D;
【解析】可求每个外角为60°,∴ 360÷60=6或 ∴ n=6.
2.【答案】A;
【解析】较长对角线与较短对角线及一边长构成一直角三角形,用勾股定理求解.
3.【答案】C;
【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2,高为3,
因而等边三角形的面积是3,
∴正六边形的面积=18,
故选C.
4.【答案】C;
【解析】当周长一定时,边数越多的正多边形其面积越大,当它成为圆时面积最大.
5.【答案】C;
【解析】五角星的每一个角所对的弧为圆的,∴ 弧的度数为72°,因而每个角的度数为36°,
故选C.
6.【答案】D.
【解析】如图③所示,正五边形ABCDE的中心角为72°,各内角为108°,故五角星五个锐角均为48°.
二、填空题
7.【答案】72°;
【解析】=360°-90°-90°-108°=72°.
8.【答案】;
【解析】如图所示,△ABC为等腰Rt△,.
9.【答案】cm;
【解析】过O作OD⊥BC于D,连接OB,在Rt△BOD中,BD=BC==5(cm).
∠BOD=,
∴ .
∴ BO=(cm).
10.【答案】54°;
【解析】连接OB,
则OB=OA,
∴∠BAO=∠ABO,
∵点O是正五边形ABCDE的中心,
∴∠AOB==72°,
∴∠BAO=(180°﹣72°)=54°;
故答案为:54°.
11.【答案】5cm,30cm,cm,;
12.【答案】2:.
【解析】设正六边形的半径是r,则外接圆的半径r, 内切圆的半径是正六边形的边心距,因而是, 因而正六边形的外接圆的半径与内切圆的半径之比为2:.
三、解答题
13.【答案与解析】
作AD⊥BC于D.
∵ △ABC是正三角形,
∴ 点O在AD上,a=BC=2CD,∠OCD=30°,
在Rt△COD中,,
,
∴ ,.
又∵ AD=OA+OD=2+1=3,
∴ ,
∴ ,,,.
14.【答案与解析】
有错误,由正六边形的每个顶点外圆要转60°角,应转了(圈).
15.【答案与解析】
解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=5×=5(cm).
即⊙O的半径R=5cm.
同课章节目录
