人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):39【基础】切线长定理(附答案)
文档属性
| 名称 | 人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):39【基础】切线长定理(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 224.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-18 22:58:00 | ||
图片预览




文档简介
切线长定理—知识讲解(基础)
【学习目标】
1.了解切线长定义;理解切线的判定和性质;理解三角形的内切圆及内心的定义;
2.掌握切线长定理;利用切线长定理解决相关的计算和证明.
【要点梳理】
要点一、切线的判定定理和性质定理
1.切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线. 要点诠释:
切线的判定方法:
(1)定义:直线和圆有唯一公共点时,这条直线就是圆的切线;
(2)定理:和圆心的距离等于半径的直线是圆的切线;
(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点,二是直线与过交点的半径垂直,缺一不可). 2.切线的性质定理: 圆的切线垂直于过切点的半径. 要点诠释:
切线的性质:
(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于过切点的半径;
(4)经过圆心垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心.
要点二、切线长定理 1.切线长: 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 要点诠释: 切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理: 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释: 切线长定理包含两个结论:线段相等和角相等.
3.圆外切四边形的性质:
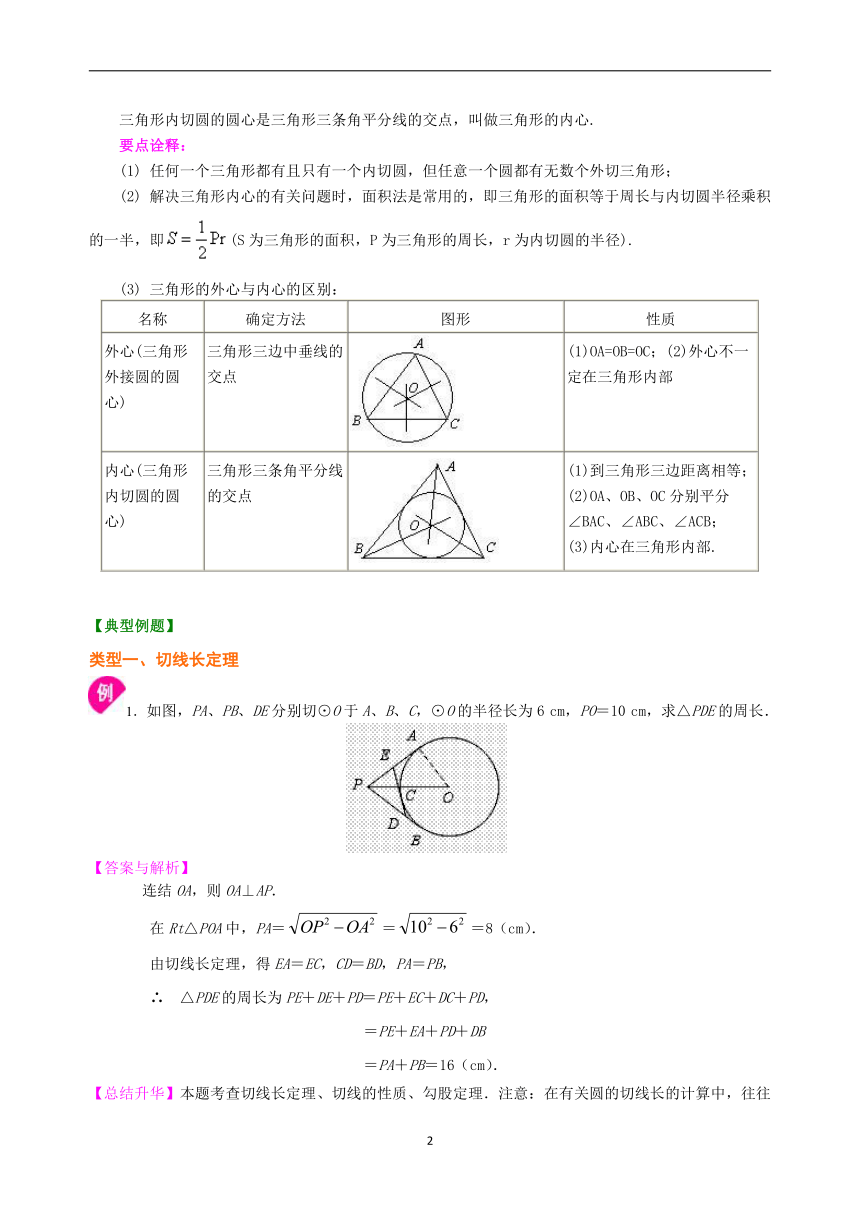
圆外切四边形的两组对边之和相等. 要点三、三角形的内切圆 1.三角形的内切圆: 与三角形各边都相切的圆叫做三角形的内切圆. 2.三角形的内心: 三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心. 要点诠释: (1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形; (2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即/(S为三角形的面积,P为三角形的周长,r为内切圆的半径). (3) 三角形的外心与内心的区别:
名称
确定方法
图形
性质
外心(三角形外接圆的圆心)
三角形三边中垂线的交点
/
(1)OA=OB=OC;(2)外心不一定在三角形内部
内心(三角形内切圆的圆心)
三角形三条角平分线的交点
/
(1)到三角形三边距离相等;(2)OA、OB、OC分别平分
∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
【典型例题】
类型一、切线长定理
/1.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径长为6 cm,PO=10 cm,求△PDE的周长.
/
【答案与解析】
连结OA,则OA⊥AP.
在Rt△POA中,PA=/=/=8(cm).
由切线长定理,得EA=EC,CD=BD,PA=PB,
∴ △PDE的周长为PE+DE+PD=PE+EC+DC+PD,
=PE+EA+PD+DB
=PA+PB=16(cm).
【总结升华】本题考查切线长定理、切线的性质、勾股定理.注意:在有关圆的切线长的计算中,往往利用切线长定理进行线段的转换.
/2.(2019?柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,∠DAE=∠ABE,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
/
【思路点拨】(1)根据圆周角定理证明∠ABC=∠ACB,得到答案;
(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.
【答案与解析】
证明:(1)∵∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
/,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
/,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
/
【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.
举一反三:
【变式】(2019?青海)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
/
【答案】(1)证明:连接OA,
∵AM是⊙O的切线,∴∠OAM=90°,
∵∠B=60°,∴∠AOC=120°,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴∠AOM=60°,∴∠M=30°,
∴∠OCA=∠M,
∴AM=AC;
(2)作AG⊥CM于G,
∵∠OCA=30°,AC=3,∴AG=/,
由勾股定理的,CG=/,
则MC=2CG=3/.
类型二、三角形的内切圆
/3.已知:如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
/ /
【答案与解析】
设内切圆与三角形的三边AB、AC、BC分别交于D、E、F,
连接OE、 OF、OD、AO、BO、CO.
∴△ABC=△AOB+△AOC+△BOC=/r(a+b+c).
【总结升华】考虑把△ABC的面积分割成3个以圆的半径为高的三角形面积的和,从而求出△ABC的面积.
举一反三:
【变式】已知如图,△ABC中,∠C=90°,BC=4,AC=3,求△ABC的内切圆⊙O的半径r.
【答案】
连结OA、OB、OC,
∵△ABC中,∠C=90°,BC=4,AC=3,∴AB=5.
则S△AOB+S△COB+S△AOC=S△ABC,即/
类型三、与相切有关的计算与证明
/4.如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD=5,求AD的长.
/
【答案与解析】
(1)结论:/与/相切
证明:连接/
∵点/、/在圆上,
∴/
∵四边形/是平行四边形,
∴/
∴/
∵/,∴/,∴/
在/和//
∴/,∴/
∵/与/相切
∴/,∴/
∴/
∴/与/相切
(2)∵/,四边形/是平行四边形
∴/,/,/
∵/,∴/,∴/
∴/ ,∴/
∴/.
【总结升华】本题虽然是圆和平行四边形的位置关系问题,但是依然考察的是如何将所有条件放在最基本的三角形中求解的能力.判断出DG与圆相切不难,难点在于如何证明.第二问则不难,重点在于如何利用角度的倍分关系来判断直角三角形中的特殊角度,从而求解.
切线长定理—巩固练习(基础)
【巩固练习】
一、选择题 1. 下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A./(a+b+c)r B.2(a+b+c) C./(a+b+c)r D.(a+b+c)r
3.(2019?黔西南州)如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
/
A.150° B.130° C.155° D.135°
4. 如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( ) A.70° B.90° C.60° D.45° / / 第4题图 第5题图
5.如图,/是/的切线,切点为A,PA=2/,∠APO=30°,则/的半径为( )
A.1 B./ C.2 D.4
6.已知如图所示,等边△ABC的边长为2/cm,下列以A为圆心的各圆中, 半径是3cm的圆是( ) /
二、填空题
7.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.
第7题图 第8题图 第9题图
8.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
9.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
10.如图,/、/分别切⊙/于点/、/,点/是⊙/上一点,且/,则/____度.
/ /
第10题图 第11题图
11.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
12.(2019?鄂州)已知点P是半径为1的⊙O外一点,PA切⊙O于点A,且PA=1,AB是⊙O的弦,AB=/,连接PB,则PB= .
三、解答题
13. 已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.求证:DE为⊙O的切线.
/
14.已知:如图,点/是⊙/的直径/延长线上一点,点/ 在⊙/上,且/
求证:/是⊙/的切线;
/
15.(2019秋?东城区月考)如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.
/
【答案与解析】
一、选择题 1.【答案】C.
【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线.
2.【答案】A.
【解析】连结内心与三个顶点,则△ABC的面积等于三个三角形的面积之和,所以△ABC的面积
为/a·r+/b·r+/c·r=/(a+b+c)r.
3.【答案】B;
【解析】∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故选B.
4.【答案】B;
【解析】由AD∥BC,得∠ADC+∠BCD=180°,又AD、DC、BC与⊙O相切,
所以∠ODC=/∠ADC,∠OCD=/∠BCD,所以∠ODC+∠OCD=/×180°=90°,所以∠DOC=90°.
故选B.
5.【答案】C;
【解析】连结OA,则∠OAP=90°,设OA=x,则OP=2x,由勾股定理可求x=2,故选C.
6.【答案】C;
【解析】易求等边△ABC的高为3cm等于圆的半径,所以圆A与BC相切,故选C.
二、填空题
7.【答案】76°;
【解析】连接ID,IF ∵∠DEF=52°, ∴∠DIF=104°,
∵D、F是切点, ∴DI⊥AB,IF⊥AC ,
∴∠ADI=∠AFI=90°, ∴∠A=1800-1040=76°.
8.【答案】52;
【解析】提示:AB+CD=AD+BC.
9.【答案】115°;
【解析】∵∠A=500 ∴∠ABC+∠ACB=130°,
∵OB,OC分别平分∠ABC,∠ACB, ∴∠OBC+∠OCB=65°,
∴∠BOC=1800-650=115°.
10.【答案】60°;
【解析】连结OA、OB,则∠AOB=120°,在四边形OAPB中,∠P=360°-90°-90°-120°=60°.
11.【答案】26°;
【解析】连结OA,则∠AOC=64°,∠P=90°-64°=26°.
12.【答案】1或/.
【解析】连接OA,
(1)如图1,连接OA,
∵PA=AO=1,OA=OB,PA是⊙的切线,
∴∠AOP=45°∵OA=OB,
∴∠BOP=∠AOP=45°,
在△POA与△POB中,/,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,连接OA,与PB交于C,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=,1
∴OP=/;
∵AB=/,
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=/,
∴BC=/,
∴PB=/.
故答案为:1或/.
三、解答题
13.【答案与解析】
如图,连接OD. ∵ D为AC中点, O为AB中点,
∴ OD为△ABC的中位线. ∴OD∥BC.
∵ DE⊥BC, ∴∠DEC=90°.
∴∠ODE=∠DEC=90°. ∴OD⊥DE于点D.
∴ DE为⊙O的切线.
14.【答案与解析】
连接/.
∵/,
∴/.
∴/是等边三角形.
∴/.
∵/,∴/.
∴/. ∴/ .
又∵点/在⊙/上,
∴/是⊙/的切线 .
15. 【答案与解析】
解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
∴PA=PB,EA=EQ,FB=FQ,
∵PA=8cm,
∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm).
【学习目标】
1.了解切线长定义;理解切线的判定和性质;理解三角形的内切圆及内心的定义;
2.掌握切线长定理;利用切线长定理解决相关的计算和证明.
【要点梳理】
要点一、切线的判定定理和性质定理
1.切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线. 要点诠释:
切线的判定方法:
(1)定义:直线和圆有唯一公共点时,这条直线就是圆的切线;
(2)定理:和圆心的距离等于半径的直线是圆的切线;
(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点,二是直线与过交点的半径垂直,缺一不可). 2.切线的性质定理: 圆的切线垂直于过切点的半径. 要点诠释:
切线的性质:
(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于过切点的半径;
(4)经过圆心垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心.
要点二、切线长定理 1.切线长: 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 要点诠释: 切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理: 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释: 切线长定理包含两个结论:线段相等和角相等.
3.圆外切四边形的性质:
圆外切四边形的两组对边之和相等. 要点三、三角形的内切圆 1.三角形的内切圆: 与三角形各边都相切的圆叫做三角形的内切圆. 2.三角形的内心: 三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心. 要点诠释: (1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形; (2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即/(S为三角形的面积,P为三角形的周长,r为内切圆的半径). (3) 三角形的外心与内心的区别:
名称
确定方法
图形
性质
外心(三角形外接圆的圆心)
三角形三边中垂线的交点
/
(1)OA=OB=OC;(2)外心不一定在三角形内部
内心(三角形内切圆的圆心)
三角形三条角平分线的交点
/
(1)到三角形三边距离相等;(2)OA、OB、OC分别平分
∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
【典型例题】
类型一、切线长定理
/1.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径长为6 cm,PO=10 cm,求△PDE的周长.
/
【答案与解析】
连结OA,则OA⊥AP.
在Rt△POA中,PA=/=/=8(cm).
由切线长定理,得EA=EC,CD=BD,PA=PB,
∴ △PDE的周长为PE+DE+PD=PE+EC+DC+PD,
=PE+EA+PD+DB
=PA+PB=16(cm).
【总结升华】本题考查切线长定理、切线的性质、勾股定理.注意:在有关圆的切线长的计算中,往往利用切线长定理进行线段的转换.
/2.(2019?柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,∠DAE=∠ABE,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
/
【思路点拨】(1)根据圆周角定理证明∠ABC=∠ACB,得到答案;
(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.
【答案与解析】
证明:(1)∵∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
/,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
/,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
/
【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.
举一反三:
【变式】(2019?青海)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
/
【答案】(1)证明:连接OA,
∵AM是⊙O的切线,∴∠OAM=90°,
∵∠B=60°,∴∠AOC=120°,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴∠AOM=60°,∴∠M=30°,
∴∠OCA=∠M,
∴AM=AC;
(2)作AG⊥CM于G,
∵∠OCA=30°,AC=3,∴AG=/,
由勾股定理的,CG=/,
则MC=2CG=3/.
类型二、三角形的内切圆
/3.已知:如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
/ /
【答案与解析】
设内切圆与三角形的三边AB、AC、BC分别交于D、E、F,
连接OE、 OF、OD、AO、BO、CO.
∴△ABC=△AOB+△AOC+△BOC=/r(a+b+c).
【总结升华】考虑把△ABC的面积分割成3个以圆的半径为高的三角形面积的和,从而求出△ABC的面积.
举一反三:
【变式】已知如图,△ABC中,∠C=90°,BC=4,AC=3,求△ABC的内切圆⊙O的半径r.
【答案】
连结OA、OB、OC,
∵△ABC中,∠C=90°,BC=4,AC=3,∴AB=5.
则S△AOB+S△COB+S△AOC=S△ABC,即/
类型三、与相切有关的计算与证明
/4.如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD=5,求AD的长.
/
【答案与解析】
(1)结论:/与/相切
证明:连接/
∵点/、/在圆上,
∴/
∵四边形/是平行四边形,
∴/
∴/
∵/,∴/,∴/
在/和//
∴/,∴/
∵/与/相切
∴/,∴/
∴/
∴/与/相切
(2)∵/,四边形/是平行四边形
∴/,/,/
∵/,∴/,∴/
∴/ ,∴/
∴/.
【总结升华】本题虽然是圆和平行四边形的位置关系问题,但是依然考察的是如何将所有条件放在最基本的三角形中求解的能力.判断出DG与圆相切不难,难点在于如何证明.第二问则不难,重点在于如何利用角度的倍分关系来判断直角三角形中的特殊角度,从而求解.
切线长定理—巩固练习(基础)
【巩固练习】
一、选择题 1. 下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A./(a+b+c)r B.2(a+b+c) C./(a+b+c)r D.(a+b+c)r
3.(2019?黔西南州)如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
/
A.150° B.130° C.155° D.135°
4. 如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( ) A.70° B.90° C.60° D.45° / / 第4题图 第5题图
5.如图,/是/的切线,切点为A,PA=2/,∠APO=30°,则/的半径为( )
A.1 B./ C.2 D.4
6.已知如图所示,等边△ABC的边长为2/cm,下列以A为圆心的各圆中, 半径是3cm的圆是( ) /
二、填空题
7.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.
第7题图 第8题图 第9题图
8.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
9.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
10.如图,/、/分别切⊙/于点/、/,点/是⊙/上一点,且/,则/____度.
/ /
第10题图 第11题图
11.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
12.(2019?鄂州)已知点P是半径为1的⊙O外一点,PA切⊙O于点A,且PA=1,AB是⊙O的弦,AB=/,连接PB,则PB= .
三、解答题
13. 已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.求证:DE为⊙O的切线.
/
14.已知:如图,点/是⊙/的直径/延长线上一点,点/ 在⊙/上,且/
求证:/是⊙/的切线;
/
15.(2019秋?东城区月考)如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.
/
【答案与解析】
一、选择题 1.【答案】C.
【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线.
2.【答案】A.
【解析】连结内心与三个顶点,则△ABC的面积等于三个三角形的面积之和,所以△ABC的面积
为/a·r+/b·r+/c·r=/(a+b+c)r.
3.【答案】B;
【解析】∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故选B.
4.【答案】B;
【解析】由AD∥BC,得∠ADC+∠BCD=180°,又AD、DC、BC与⊙O相切,
所以∠ODC=/∠ADC,∠OCD=/∠BCD,所以∠ODC+∠OCD=/×180°=90°,所以∠DOC=90°.
故选B.
5.【答案】C;
【解析】连结OA,则∠OAP=90°,设OA=x,则OP=2x,由勾股定理可求x=2,故选C.
6.【答案】C;
【解析】易求等边△ABC的高为3cm等于圆的半径,所以圆A与BC相切,故选C.
二、填空题
7.【答案】76°;
【解析】连接ID,IF ∵∠DEF=52°, ∴∠DIF=104°,
∵D、F是切点, ∴DI⊥AB,IF⊥AC ,
∴∠ADI=∠AFI=90°, ∴∠A=1800-1040=76°.
8.【答案】52;
【解析】提示:AB+CD=AD+BC.
9.【答案】115°;
【解析】∵∠A=500 ∴∠ABC+∠ACB=130°,
∵OB,OC分别平分∠ABC,∠ACB, ∴∠OBC+∠OCB=65°,
∴∠BOC=1800-650=115°.
10.【答案】60°;
【解析】连结OA、OB,则∠AOB=120°,在四边形OAPB中,∠P=360°-90°-90°-120°=60°.
11.【答案】26°;
【解析】连结OA,则∠AOC=64°,∠P=90°-64°=26°.
12.【答案】1或/.
【解析】连接OA,
(1)如图1,连接OA,
∵PA=AO=1,OA=OB,PA是⊙的切线,
∴∠AOP=45°∵OA=OB,
∴∠BOP=∠AOP=45°,
在△POA与△POB中,/,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,连接OA,与PB交于C,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=,1
∴OP=/;
∵AB=/,
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=/,
∴BC=/,
∴PB=/.
故答案为:1或/.
三、解答题
13.【答案与解析】
如图,连接OD. ∵ D为AC中点, O为AB中点,
∴ OD为△ABC的中位线. ∴OD∥BC.
∵ DE⊥BC, ∴∠DEC=90°.
∴∠ODE=∠DEC=90°. ∴OD⊥DE于点D.
∴ DE为⊙O的切线.
14.【答案与解析】
连接/.
∵/,
∴/.
∴/是等边三角形.
∴/.
∵/,∴/.
∴/. ∴/ .
又∵点/在⊙/上,
∴/是⊙/的切线 .
15. 【答案与解析】
解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
∴PA=PB,EA=EQ,FB=FQ,
∵PA=8cm,
∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm).
同课章节目录
