人教版七年级数学上册第四章几何图形:4.3.3 余角和补角 课件(共18张PPT)
文档属性
| 名称 | 人教版七年级数学上册第四章几何图形:4.3.3 余角和补角 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 10:58:36 | ||
图片预览





文档简介
(共18张PPT)
第四章 几何图形初步
4.3.3
余角和补角
学习目标
?掌握互余、互补的概念和性质.
?能在图中识别互余和互补的角.
?能用方程思想解决几何中角的计算问题.
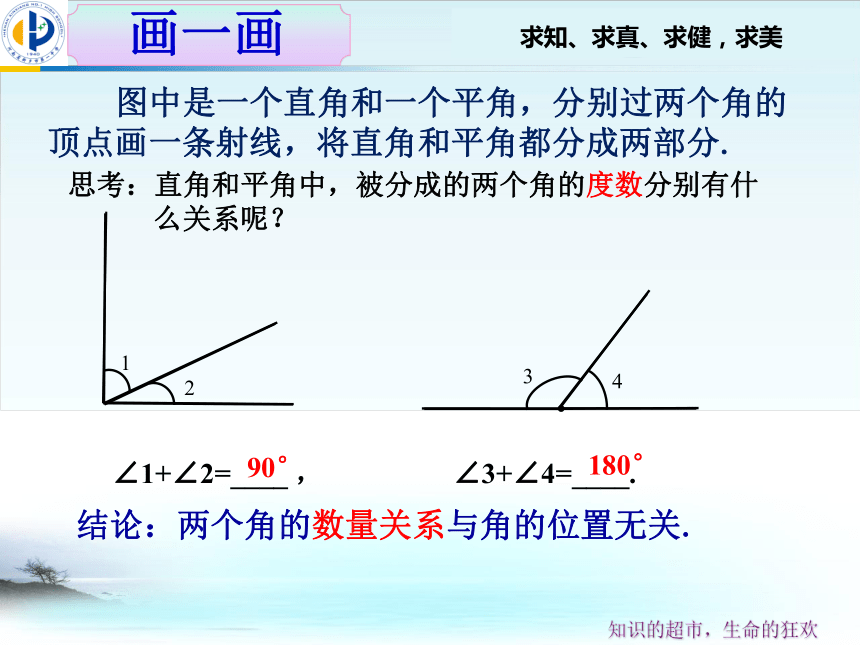
图中是一个直角和一个平角,分别过两个角的
顶点画一条射线,将直角和平角都分成两部分.
∠1+∠2=____ , ∠3+∠4=____.
90°
180°
画一画
结论:两个角的数量关系与角的位置无关.
思考:直角和平角中,被分成的两个角的度数分别有什
么关系呢?
∠1+∠2=____ , ∠3+∠4=____.
90°
180°
概念学习
(1)如果两个角的和等于90°(直角),则这两个角互为余角.
(2)如果两个角的和等于180°(平角),则这两个角互为补角.
(简称互余)
(简称互补)
判断:1.因为∠1+∠2=90°,所以∠1是余角( )
2.互补或者互余的两个角一定是相邻的.( )
3.如果∠1与∠2互补,则∠1=180°-∠2. ( )
×
×
√
一起闯关
Are you ready?
开始!
概念理解关
性质探究关
合作展示关
第1关:概念理解
互余、互补指的都是两个角的数量关系.
从表格中你能发现什么结论或规律吗?
①只有锐角才有余角;
②一个角(锐角)的补角比余角大 90°
58°
55°
103°
13°
148°
180°-x°
90°-x°
恭喜大家!
闯关成功!
补角的性质
余角的性质
因为∠1与∠2互补、
∠3与∠4互补
且 ∠1= ∠3,
第2关:性质探究
请大家拿起手中的卡片,拼一拼平角,你有几种拼法呢?
同角的余角相等.
同角的补角相等.
如果∠1与∠2互补,∠1与∠3互补 ,试说明∠2=∠3.
因为∠1与∠2、∠3都互补
所以∠2=__________,
∠3=___________.
所以∠2=∠3
如果∠1与∠2互余,∠1与∠3互余 ,试说明∠2=∠3.
因为∠1与∠2、∠3都互余
所以∠2= __________ ,
∠3= __________.
所以∠2=∠3
90°-∠1
90°-∠1
所以________.
等角的余角相等.
等角的补角相等.
因为∠1与∠2互余、
∠3与∠4互余
且 ∠1= ∠3,
所以________.
∠2=∠4
∠2=∠4
180°-∠1
180°-∠1
恭喜大家!
闯关成功!
第3关:合作展示
说明:
展示:小组代表以板书的形式将小组所讨论出的结果展示在黑板上.
要求板书工整.
点评讲解:小组代表以口头形式讲解解题思路,指出展示小组板书结果的不足之处.
要求声音洪亮,落落大方,扮演“小老师”.
5分钟讨论合作并展示
合作展示 展示 点评
第1题
第2题
第3题
合作展示 展示板书 点评讲解
第1题 第1组 第4组
第2题 第5组 第2组
第3题 第6组 第8组
1.如下图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,
(1)∠AOC与∠BOC的关系是什么?
互补
(2)图中有哪几对相等的角?
因为OD平分∠AOC,所以∠1=∠2,
同理,∠3=∠4
(3)图中有哪几对互余的角?
∠2和∠3, ∠1和∠4, ∠1和∠3, ∠2和∠4.
第3关:合作展示
理由:由(1)可知∠1+∠2+∠3+∠4=180°
由(2)可知 ∠1+∠3=∠2+∠4=∠1+∠4=∠2+∠3=90°
2.若一个角的补角是这个角的余角的4倍,求这个角.
解:设这个角是x°,
则 180-x= 4 ( 90-x)
解得x = 60
答:这个角是60°.
第3关:合作展示
用方程思想解决几何中角的计算问题.
∠1=∠A ,∠2=∠B
因为∠1与∠2互余
∠A与∠2互余
所以∠1=∠A
(同角的余角相等)
因为∠1与∠2互余
∠1与∠B互余
所以∠2=∠B
(同角的余角相等)
3.请认真观察右图,回答下列问题:
(1)图中有哪几对互余的角?
∠1与∠2, ∠1与∠B
∠A与∠2, ∠A与∠B
(2)图中除直角外,哪几对是相等
的角?
恭喜大家!
闯关成功!
第3关:合作展示
课堂小结
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角的余角相等.
等角的余角相等.
同角的补角相等.
等角的补角相等.
锐角的余角和补角相差90°
用方程思想解决几何中角的计算问题.
本节课你学到了什么……?
角的关系 互余 互补
定义
(数量关系)
对应图形
性 质
问题解决
要得到摔碎的冰块上∠1、∠3的度数,我们该如何测量呢?
可以测量∠2和∠4,
则∠1=90°-∠2
∠3=180°-∠4
当堂检测
1.互余且相等的两个角的度数分别是___________.
2.一个锐角的补角比它的余角大 ____度.
3.如果∠1+∠2=180°,∠2+∠3=180°,那么∠1与∠3的关系是( )
(A)互补 (B)互余 (C)相等 (D)不能确定
4.如果∠1与∠2互余,∠3与∠4互余,并且∠1=∠3,
则可知∠2=∠4.依据的是( )
(A)同角的补角相等 (B)等角的补角相等
(C)同角的余角相等 (D)等角的余角相等
45°、45°
90
C
D
课后作业
必做题:
课本第139页练习2、3、4题,
习题4.3的第7、11题.
研究性作业(选作):
先用量角器作一个40°的角,然后用不同方法作出它的补角和余角.
同学们
再 见
谢 谢
不是已懂得知识
给我最大快乐的
而是继续不断地
而是不断地学习
不是已有的东西
而是不断地获取
不是已达到的高度
攀登!
高斯
第四章 几何图形初步
4.3.3
余角和补角
学习目标
?掌握互余、互补的概念和性质.
?能在图中识别互余和互补的角.
?能用方程思想解决几何中角的计算问题.
图中是一个直角和一个平角,分别过两个角的
顶点画一条射线,将直角和平角都分成两部分.
∠1+∠2=____ , ∠3+∠4=____.
90°
180°
画一画
结论:两个角的数量关系与角的位置无关.
思考:直角和平角中,被分成的两个角的度数分别有什
么关系呢?
∠1+∠2=____ , ∠3+∠4=____.
90°
180°
概念学习
(1)如果两个角的和等于90°(直角),则这两个角互为余角.
(2)如果两个角的和等于180°(平角),则这两个角互为补角.
(简称互余)
(简称互补)
判断:1.因为∠1+∠2=90°,所以∠1是余角( )
2.互补或者互余的两个角一定是相邻的.( )
3.如果∠1与∠2互补,则∠1=180°-∠2. ( )
×
×
√
一起闯关
Are you ready?
开始!
概念理解关
性质探究关
合作展示关
第1关:概念理解
互余、互补指的都是两个角的数量关系.
从表格中你能发现什么结论或规律吗?
①只有锐角才有余角;
②一个角(锐角)的补角比余角大 90°
58°
55°
103°
13°
148°
180°-x°
90°-x°
恭喜大家!
闯关成功!
补角的性质
余角的性质
因为∠1与∠2互补、
∠3与∠4互补
且 ∠1= ∠3,
第2关:性质探究
请大家拿起手中的卡片,拼一拼平角,你有几种拼法呢?
同角的余角相等.
同角的补角相等.
如果∠1与∠2互补,∠1与∠3互补 ,试说明∠2=∠3.
因为∠1与∠2、∠3都互补
所以∠2=__________,
∠3=___________.
所以∠2=∠3
如果∠1与∠2互余,∠1与∠3互余 ,试说明∠2=∠3.
因为∠1与∠2、∠3都互余
所以∠2= __________ ,
∠3= __________.
所以∠2=∠3
90°-∠1
90°-∠1
所以________.
等角的余角相等.
等角的补角相等.
因为∠1与∠2互余、
∠3与∠4互余
且 ∠1= ∠3,
所以________.
∠2=∠4
∠2=∠4
180°-∠1
180°-∠1
恭喜大家!
闯关成功!
第3关:合作展示
说明:
展示:小组代表以板书的形式将小组所讨论出的结果展示在黑板上.
要求板书工整.
点评讲解:小组代表以口头形式讲解解题思路,指出展示小组板书结果的不足之处.
要求声音洪亮,落落大方,扮演“小老师”.
5分钟讨论合作并展示
合作展示 展示 点评
第1题
第2题
第3题
合作展示 展示板书 点评讲解
第1题 第1组 第4组
第2题 第5组 第2组
第3题 第6组 第8组
1.如下图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,
(1)∠AOC与∠BOC的关系是什么?
互补
(2)图中有哪几对相等的角?
因为OD平分∠AOC,所以∠1=∠2,
同理,∠3=∠4
(3)图中有哪几对互余的角?
∠2和∠3, ∠1和∠4, ∠1和∠3, ∠2和∠4.
第3关:合作展示
理由:由(1)可知∠1+∠2+∠3+∠4=180°
由(2)可知 ∠1+∠3=∠2+∠4=∠1+∠4=∠2+∠3=90°
2.若一个角的补角是这个角的余角的4倍,求这个角.
解:设这个角是x°,
则 180-x= 4 ( 90-x)
解得x = 60
答:这个角是60°.
第3关:合作展示
用方程思想解决几何中角的计算问题.
∠1=∠A ,∠2=∠B
因为∠1与∠2互余
∠A与∠2互余
所以∠1=∠A
(同角的余角相等)
因为∠1与∠2互余
∠1与∠B互余
所以∠2=∠B
(同角的余角相等)
3.请认真观察右图,回答下列问题:
(1)图中有哪几对互余的角?
∠1与∠2, ∠1与∠B
∠A与∠2, ∠A与∠B
(2)图中除直角外,哪几对是相等
的角?
恭喜大家!
闯关成功!
第3关:合作展示
课堂小结
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角的余角相等.
等角的余角相等.
同角的补角相等.
等角的补角相等.
锐角的余角和补角相差90°
用方程思想解决几何中角的计算问题.
本节课你学到了什么……?
角的关系 互余 互补
定义
(数量关系)
对应图形
性 质
问题解决
要得到摔碎的冰块上∠1、∠3的度数,我们该如何测量呢?
可以测量∠2和∠4,
则∠1=90°-∠2
∠3=180°-∠4
当堂检测
1.互余且相等的两个角的度数分别是___________.
2.一个锐角的补角比它的余角大 ____度.
3.如果∠1+∠2=180°,∠2+∠3=180°,那么∠1与∠3的关系是( )
(A)互补 (B)互余 (C)相等 (D)不能确定
4.如果∠1与∠2互余,∠3与∠4互余,并且∠1=∠3,
则可知∠2=∠4.依据的是( )
(A)同角的补角相等 (B)等角的补角相等
(C)同角的余角相等 (D)等角的余角相等
45°、45°
90
C
D
课后作业
必做题:
课本第139页练习2、3、4题,
习题4.3的第7、11题.
研究性作业(选作):
先用量角器作一个40°的角,然后用不同方法作出它的补角和余角.
同学们
再 见
谢 谢
不是已懂得知识
给我最大快乐的
而是继续不断地
而是不断地学习
不是已有的东西
而是不断地获取
不是已达到的高度
攀登!
高斯
