高中数学人A教版必修4课件:2.2-平面向量的线性运算(共39张PPT)
文档属性
| 名称 | 高中数学人A教版必修4课件:2.2-平面向量的线性运算(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 08:57:20 | ||
图片预览









文档简介
(共39张PPT)
第二章 平面向量
2.2 平面向量的线性运算
2.2.1 向量加法运算及其几何意义
2.2.2 向量减法运算及其几何意义
2.2.3 向量数乘运算及其几何意义
下一页
2.2.1向量加法运算及其几何意义
首 页
上一页
下一页
物理学中,两次位移 的结果和位移 是相同的。
2. 物理学中,作用于物体同一点的两个不共线的合力如何求得?
3. 两个向量的合成可用“平行四边形法则”和“三角形法则”求出,本节将研究向量的加法。
首 页
上一页
下一页
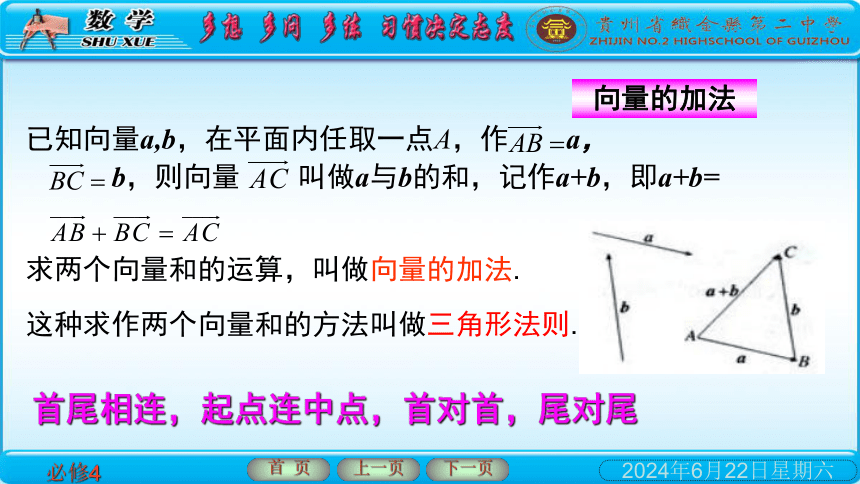
已知向量a,b,在平面内任取一点A,作 a,
b,则向量 叫做a与b的和,记作a+b,即a+b=
求两个向量和的运算,叫做向量的加法.
这种求作两个向量和的方法叫做三角形法则.
向量的加法
首 页
上一页
下一页
首尾相连,起点连中点,首对首,尾对尾
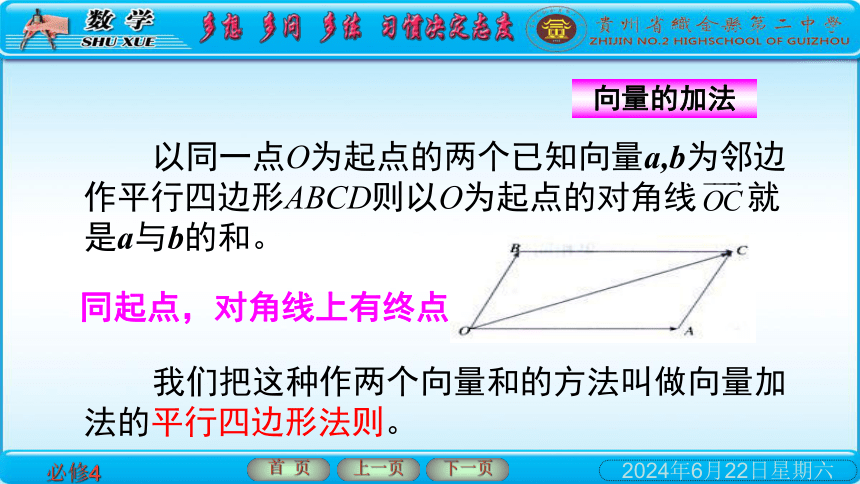
以同一点O为起点的两个已知向量a,b为邻边作平行四边形ABCD则以O为起点的对角线 就是a与b的和。
我们把这种作两个向量和的方法叫做向量加法的平行四边形法则。
向量的加法
首 页
上一页
下一页
同起点,对角线上有终点
对于零向量与任一向量a,
规定a+0=0+a=a
向量的加法
首 页
上一页
下一页
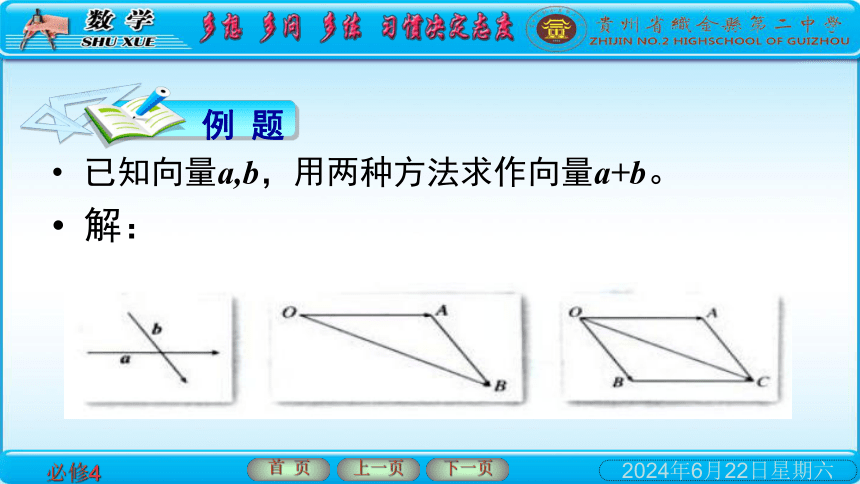
已知向量a,b,用两种方法求作向量a+b。
解:
首 页
上一页
下一页
当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?
首 页
上一页
下一页
两个向量的和仍是一个向量。
当a,b不共线时,a+b的方向与a、b都不同向,且|a+b|<|a|+|b|.
当a与b共线时,若a与b同向,则a+b的方向与a、b同向,且|a+b|=|a|+|b|.
若a与b反向,当|a|>|b|时,a+b的方向与a相同,且|a+b|=|a|-|b|;当|a|<|b|时,a+b的方向与b相同,且|a+b|=|b|-|a|.
首 页
上一页
下一页
数的加法满足交换律与结合律,
即对任意a,b?R,有a+b=b+a,(a+b)+c=a+(b+c).
任意向量a,b的加法是否也满足交换律和结合律?
首 页
上一页
下一页
作图验证
首 页
上一页
下一页
一艘船以 km/h的速度向垂直于对岸的方向行驶,同时河水的流速为2km/h,求船实际航行速度的大小与方向(用与流速间的夹角表示)。
首 页
上一页
下一页
摩托艇是抗洪抢险中的主要交通工具,设它在静水中的航行速度是每小时25千米,如果当时的水流速度是每小时15千米,那么该摩托艇向下游航行时,每小时能行________千米,它向上游航行时,每小时能行___________千米.
40
10
首 页
上一页
下一页
2.2.2向量减法运算及其几何意义
首 页
上一页
下一页
减去一个数等于加上这个数的相反数,向量的减法是否也有类似的法则?
向量的减法
首 页
上一页
下一页
相反向量
规定与a长度相等,方向相反的向量叫做a的相反向量,记作-a,显然-(-a)=a,
规定,零向量的相反向量仍是零向量。
向量的减法
首 页
上一页
下一页
向量减法的定义
任一向量与其相反向量的和是零向量, 即 a+(-a)=(-a)+a=0,所以,如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0,
定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量。
向量的减法
首 页
上一页
下一页
运算法则
已知a、b, a-b可以表示为从向量b的终点指向被减向量a的终点的向量.
已知向量a、b、c、d,求作向量a-b,c-d.
解:
向量的减法
同起点
连终点
指被减
首 页
上一页
下一页
首 页
上一页
下一页
判断下列等式是否成立:
(1)a+b=b+a ( )
(2)a-b=b-a ( )
(3)0-a=a ( )
(4)-(-a)=a ( )
(5)a+(-a)=0 ( )
?
?
?
?
?
首 页
上一页
下一页
1.在学习向量加法概念时,要结合物理学理解向量加法的意义;
2.要熟练地掌握向量加法的平行四边形法则和三角形法则,并能做出已知两个向量的和向量;
3.要理解向量加法的交换律和结合律,能说出这两个向量运算律的几何意义;
4.理解向量减法的意义;能作出两个向量的差向量。
首 页
上一页
下一页
习题2.2 A组 1、2、3、4、6、7、8
首 页
上一页
下一页
2.2.3 向量数乘运算及其几何意义
首 页
上一页
下一页
已知非零向量a,作出a+a+a和(-a)+(-a)+(-a),并说明它们的几何意义.
把a+a+a记作3a,显然3a的方向与a的方向相同,3a的长度是a的3倍,即|3a|=3|a|.
同样,(-a)+(-a)+(-a)=3(-a),显然3(-a)的方向与a的方向相反,3(-a)的长度是a的3倍,这样3(-a)=-3a.
向量的数乘
首 页
上一页
下一页
实数?与向量a的积是一个向量,称为向量的数乘,记作?a,它的长度与方向规定如下:
(1)|?a|=|?||a|;
(2)当?>0时,?a的方向与向量a的方向相同;当?<0时,?a的方向与a的方向相反.
向量的数乘
首 页
上一页
下一页
特别地,
当?=0或a=0时,?a=0;
当?=-1时,(-1)?a=-a,就是a的相反向量.
向量的数乘
首 页
上一页
下一页
实数与向量的积的运算律
设?、?为实数,那么
(1)?(?a)=( ??)a;(结合律)
(2)(?+?)a=?a+?a;(第一分配律)
(3)?(a+b)= ?a+?b.(第二分配律)
特别地,有(-?)a=-(?a)= ?(-a),?(a-b)=?a-?b.
向量的数乘
首 页
上一页
下一页
计算:
(1)(-3)?4a;
(2)3(a+b)-2(a-b)-a;
(3)(2a+3b-c)-(3a-2b+c).
首 页
上一页
下一页
引入向量数乘运算后,你能发现数乘向量与原向量之间的位置关系吗?
首 页
上一页
下一页
对于向量a(a?0)、b,如果有一个实数?,使b=?a,那么由向量数乘的定义知:a与b共线;
反过来,已知向量a与b共线,a?0,且向量b的长度是向量a的长度的?倍,即|b|=?|a|,那么当a与b同向时,有b=?a,当a与b反向时,有b=-?a.
首 页
上一页
下一页
向量共线定理:
向量a(a?0)与b共线,当且仅当有唯一一个实数?,使b=?a.
首 页
上一页
下一页
OA
首 页
上一页
下一页
向量的线性运算
向量的加、减、数乘运算统称为向量的线性运算,
对于任意向量a、b,以及任意实数?、?1、?2,
恒有 ?(?1a??2b)= ??1a???2b.
首 页
上一页
下一页
首 页
上一页
下一页
练习1 课本P.100 1、2、3、4
练习2 设a、b是两个不平行的向量,且x(2a+b) +y(3a-2b)=7a , x,y?R,
则x=____,y=_____.
2
1
首 页
上一页
下一页
首 页
上一页
下一页
1. 理解实数与向量的积的意义,能说出实数与 一个向量的积的模及方向与这个向量的模及方向
间的关系;
2. 能说出实数与向量的积的三条运算律,并会运用它们进行计算;
首 页
上一页
下一页
3. 能表述一个向量与非零向量共线的充要条件;
4. 会表示与非零向量共线的向量,会判断两个向
量共线.
首 页
上一页
下一页
(1)习题2.2 A组5、9、10、11、12、13.
(2)完成固学案相应的内容,熟悉向量运算.
首 页
上一页
第二章 平面向量
2.2 平面向量的线性运算
2.2.1 向量加法运算及其几何意义
2.2.2 向量减法运算及其几何意义
2.2.3 向量数乘运算及其几何意义
下一页
2.2.1向量加法运算及其几何意义
首 页
上一页
下一页
物理学中,两次位移 的结果和位移 是相同的。
2. 物理学中,作用于物体同一点的两个不共线的合力如何求得?
3. 两个向量的合成可用“平行四边形法则”和“三角形法则”求出,本节将研究向量的加法。
首 页
上一页
下一页
已知向量a,b,在平面内任取一点A,作 a,
b,则向量 叫做a与b的和,记作a+b,即a+b=
求两个向量和的运算,叫做向量的加法.
这种求作两个向量和的方法叫做三角形法则.
向量的加法
首 页
上一页
下一页
首尾相连,起点连中点,首对首,尾对尾
以同一点O为起点的两个已知向量a,b为邻边作平行四边形ABCD则以O为起点的对角线 就是a与b的和。
我们把这种作两个向量和的方法叫做向量加法的平行四边形法则。
向量的加法
首 页
上一页
下一页
同起点,对角线上有终点
对于零向量与任一向量a,
规定a+0=0+a=a
向量的加法
首 页
上一页
下一页
已知向量a,b,用两种方法求作向量a+b。
解:
首 页
上一页
下一页
当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?
首 页
上一页
下一页
两个向量的和仍是一个向量。
当a,b不共线时,a+b的方向与a、b都不同向,且|a+b|<|a|+|b|.
当a与b共线时,若a与b同向,则a+b的方向与a、b同向,且|a+b|=|a|+|b|.
若a与b反向,当|a|>|b|时,a+b的方向与a相同,且|a+b|=|a|-|b|;当|a|<|b|时,a+b的方向与b相同,且|a+b|=|b|-|a|.
首 页
上一页
下一页
数的加法满足交换律与结合律,
即对任意a,b?R,有a+b=b+a,(a+b)+c=a+(b+c).
任意向量a,b的加法是否也满足交换律和结合律?
首 页
上一页
下一页
作图验证
首 页
上一页
下一页
一艘船以 km/h的速度向垂直于对岸的方向行驶,同时河水的流速为2km/h,求船实际航行速度的大小与方向(用与流速间的夹角表示)。
首 页
上一页
下一页
摩托艇是抗洪抢险中的主要交通工具,设它在静水中的航行速度是每小时25千米,如果当时的水流速度是每小时15千米,那么该摩托艇向下游航行时,每小时能行________千米,它向上游航行时,每小时能行___________千米.
40
10
首 页
上一页
下一页
2.2.2向量减法运算及其几何意义
首 页
上一页
下一页
减去一个数等于加上这个数的相反数,向量的减法是否也有类似的法则?
向量的减法
首 页
上一页
下一页
相反向量
规定与a长度相等,方向相反的向量叫做a的相反向量,记作-a,显然-(-a)=a,
规定,零向量的相反向量仍是零向量。
向量的减法
首 页
上一页
下一页
向量减法的定义
任一向量与其相反向量的和是零向量, 即 a+(-a)=(-a)+a=0,所以,如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0,
定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量。
向量的减法
首 页
上一页
下一页
运算法则
已知a、b, a-b可以表示为从向量b的终点指向被减向量a的终点的向量.
已知向量a、b、c、d,求作向量a-b,c-d.
解:
向量的减法
同起点
连终点
指被减
首 页
上一页
下一页
首 页
上一页
下一页
判断下列等式是否成立:
(1)a+b=b+a ( )
(2)a-b=b-a ( )
(3)0-a=a ( )
(4)-(-a)=a ( )
(5)a+(-a)=0 ( )
?
?
?
?
?
首 页
上一页
下一页
1.在学习向量加法概念时,要结合物理学理解向量加法的意义;
2.要熟练地掌握向量加法的平行四边形法则和三角形法则,并能做出已知两个向量的和向量;
3.要理解向量加法的交换律和结合律,能说出这两个向量运算律的几何意义;
4.理解向量减法的意义;能作出两个向量的差向量。
首 页
上一页
下一页
习题2.2 A组 1、2、3、4、6、7、8
首 页
上一页
下一页
2.2.3 向量数乘运算及其几何意义
首 页
上一页
下一页
已知非零向量a,作出a+a+a和(-a)+(-a)+(-a),并说明它们的几何意义.
把a+a+a记作3a,显然3a的方向与a的方向相同,3a的长度是a的3倍,即|3a|=3|a|.
同样,(-a)+(-a)+(-a)=3(-a),显然3(-a)的方向与a的方向相反,3(-a)的长度是a的3倍,这样3(-a)=-3a.
向量的数乘
首 页
上一页
下一页
实数?与向量a的积是一个向量,称为向量的数乘,记作?a,它的长度与方向规定如下:
(1)|?a|=|?||a|;
(2)当?>0时,?a的方向与向量a的方向相同;当?<0时,?a的方向与a的方向相反.
向量的数乘
首 页
上一页
下一页
特别地,
当?=0或a=0时,?a=0;
当?=-1时,(-1)?a=-a,就是a的相反向量.
向量的数乘
首 页
上一页
下一页
实数与向量的积的运算律
设?、?为实数,那么
(1)?(?a)=( ??)a;(结合律)
(2)(?+?)a=?a+?a;(第一分配律)
(3)?(a+b)= ?a+?b.(第二分配律)
特别地,有(-?)a=-(?a)= ?(-a),?(a-b)=?a-?b.
向量的数乘
首 页
上一页
下一页
计算:
(1)(-3)?4a;
(2)3(a+b)-2(a-b)-a;
(3)(2a+3b-c)-(3a-2b+c).
首 页
上一页
下一页
引入向量数乘运算后,你能发现数乘向量与原向量之间的位置关系吗?
首 页
上一页
下一页
对于向量a(a?0)、b,如果有一个实数?,使b=?a,那么由向量数乘的定义知:a与b共线;
反过来,已知向量a与b共线,a?0,且向量b的长度是向量a的长度的?倍,即|b|=?|a|,那么当a与b同向时,有b=?a,当a与b反向时,有b=-?a.
首 页
上一页
下一页
向量共线定理:
向量a(a?0)与b共线,当且仅当有唯一一个实数?,使b=?a.
首 页
上一页
下一页
OA
首 页
上一页
下一页
向量的线性运算
向量的加、减、数乘运算统称为向量的线性运算,
对于任意向量a、b,以及任意实数?、?1、?2,
恒有 ?(?1a??2b)= ??1a???2b.
首 页
上一页
下一页
首 页
上一页
下一页
练习1 课本P.100 1、2、3、4
练习2 设a、b是两个不平行的向量,且x(2a+b) +y(3a-2b)=7a , x,y?R,
则x=____,y=_____.
2
1
首 页
上一页
下一页
首 页
上一页
下一页
1. 理解实数与向量的积的意义,能说出实数与 一个向量的积的模及方向与这个向量的模及方向
间的关系;
2. 能说出实数与向量的积的三条运算律,并会运用它们进行计算;
首 页
上一页
下一页
3. 能表述一个向量与非零向量共线的充要条件;
4. 会表示与非零向量共线的向量,会判断两个向
量共线.
首 页
上一页
下一页
(1)习题2.2 A组5、9、10、11、12、13.
(2)完成固学案相应的内容,熟悉向量运算.
首 页
上一页
